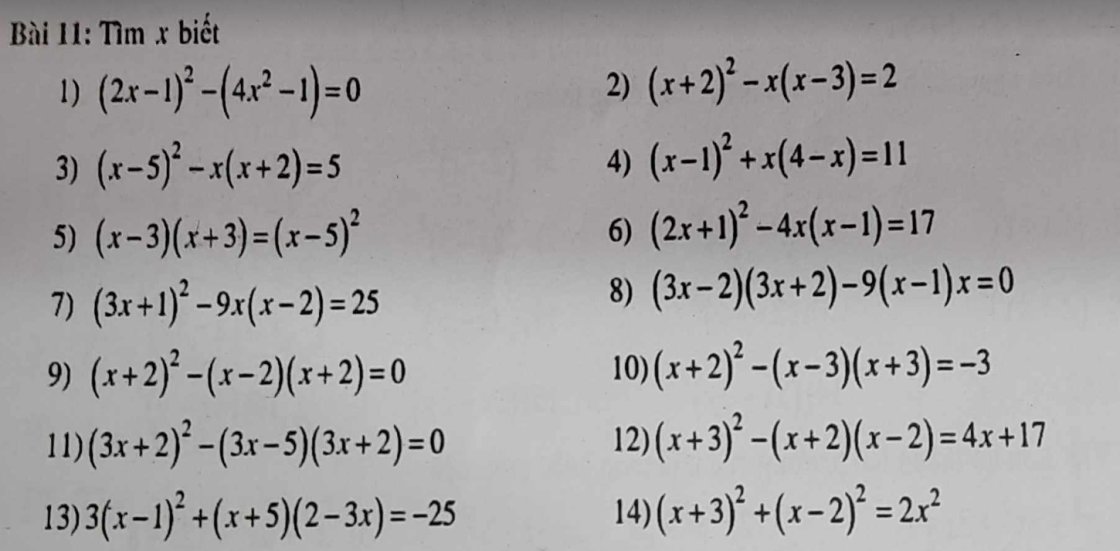1: \(\left(2x-1\right)^2-\left(4x^2-1\right)=0\)

=>\(\left(2x-1\right)^2-\left(2x-1\right)\left(2x+1\right)=0\)

=>\(\left(2x-1\right)\left(2x-1-2x-1\right)=0\)

=>-2(2x-1)=0

=>2x-1=0

=>\(x=\dfrac{1}{2}\)

2: \(\left(x+2\right)^2-x\left(x-3\right)=2\)

=>\(x^2+4x+4-x^2+3x=2\)

=>7x+4=2

=>7x=-2

=>\(x=-\dfrac{2}{7}\)

3: \(\left(x-5\right)^2-x\left(x+2\right)=5\)

=>\(x^2-10x+25-x^2-2x=5\)

=>-12x+25=5

=>-12x=5-25=-20

=>\(x=\dfrac{20}{12}=\dfrac{5}{3}\)

4: \(\left(x-1\right)^2+x\left(4-x\right)=11\)

=>\(x^2-2x+1+4x-x^2=11\)

=>2x+1=11

=>2x=10

=>x=5

5: \(\left(x-3\right)\left(x+3\right)=\left(x-5\right)^2\)

=>\(x^2-9=x^2-10x+25\)

=>-10x+25=-9

=>-10x=-25-9=-34

=>\(x=\dfrac{34}{10}=\dfrac{17}{5}\)

6: \(\left(2x+1\right)^2-4x\left(x-1\right)=17\)

=>\(4x^2+4x+1-4x^2+4x=17\)

=>8x+1=17

=>8x=16

=>x=2

7: \(\left(3x+1\right)^2-9x\left(x-2\right)=25\)

=>\(9x^2+6x+1-9x^2+18x=25\)

=>24x+1=25

=>24x=24

=>x=1

8: \(\left(3x-2\right)\left(3x+2\right)-9x\left(x-1\right)=0\)

=>\(9x^2-4-9x^2+9x=0\)

=>9x-4=0

=>9x=4

=>\(x=\dfrac{4}{9}\)

9: \(\left(x+2\right)^2-\left(x-2\right)\left(x+2\right)=0\)

=>(x+2)(x+2-x+2)=0

=>4(x+2)=0

=>x+2=0

=>x=-2

10: \(\left(x+2\right)^2-\left(x-3\right)\left(x+3\right)=-3\)

=>\(x^2+4x+4-\left(x^2-9\right)+3=0\)

=>\(x^2+4x+7-x^2+9=0\)

=>4x+16=0

=>4x=-16

=>x=-4

11: \(\left(3x+2\right)^2-\left(3x-5\right)\left(3x+2\right)=0\)

=>(3x+2)(3x+2-3x+5)=0

=>7(3x+2)=0

=>3x+2=0

=>3x=-2

=>\(x=-\dfrac{2}{3}\)

12: \(\left(x+3\right)^2-\left(x+2\right)\left(x-2\right)=4x+17\)

=>\(x^2+6x+9-x^2+4=4x+17\)

=>6x+13=4x+17

=>2x=4

=>x=2

13: \(3\left(x-1\right)^2+\left(x+5\right)\left(-3x+2\right)=-25\)

=>\(3\left(x^2-2x+1\right)+2x-3x^2+10-15x=-25\)

=>\(3x^2-6x+3-3x^2-13x+10=-25\)

=>-19x+13=-25

=>-19x=-38

=>x=2

14: \(\left(x+3\right)^2+\left(x-2\right)^2=2x^2\)

=>\(x^2+6x+9+x^2-4x+4=2x^2\)

=>2x=-13

=>\(x=-\dfrac{13}{2}\)

Đây là dạng toán nâng cao chuyên đề chuyển số thập phân thành phân số, hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau: 

Bài 5:

0,300 = 0,3 = \(\dfrac{3}{10}\) = \(\dfrac{3\times100}{10\times100}\) = \(\dfrac{300}{1000}\) (bạn Hà viết đúng)

0,300 = 0,3 = \(\dfrac{3}{10}\) > \(\dfrac{3}{1000}\)  (bạn Hạnh viết sai)

0,300 = 0,3  = \(\dfrac{3}{10}\) = \(\dfrac{3\times10}{10\times10}\) = \(\dfrac{30}{100}\) (bạn Lâm viết viết đúng)

Vậy bạn viết sai là bạn Hạnh

Chọn B. Bạn Hạnh

\(\left(13-x\right)\cdot28=56\\ 13-x=56:28\\ 13-x=2\\ x=13-2\\ x=11\)

Vậy x=11

$\color{#6495ED}{\text{(13 - x).28 = 56}}$

$\color{#6495ED}{\text{(13 - x)      = 56 : 28}}$

$\color{#6495ED}{\text{  13 - x      = 2}}$

$\color{#6495ED}{\text{         x      = 13 - 2}}$

$\color{#6495ED}{\text{         x      = 11}}$

Vậy \(x=11\)

$\color{#6495ED}{\text{4}}$$\color{#87CEFA}{\text{5}}$$\color{#ADD8E6}{\text{6}}$

Bài 3. Số thập phân nào dưới đây được viết dưới dạng gọn nhất?

A. 60,06   B. 6,060   C. 60,600   D. 600,600

A nha

a = 35, b = 28

a) 

\(P=4x^4+y^4\\ =4x^4+4x^2y^2+y^4-4x^2y^2\\ =\left(4x^4+4x^2y^2+y^2\right)-4x^2y^2\\ =\left(2x^2+y^2\right)^2-\left(2xy\right)^2\\ =\left(2x^2-2xy+y^2\right)\left(2x^2+2xy+y^2\right)\) 

b) 

\(Q=x^4+64\\ =x^4+16x^2+64-16x^2\\ =\left(x^4+16x^2+64\right)-16x^2\\ =\left(x^2+8\right)^2-\left(4x\right)^2\\ =\left(x^2-4x+8\right)\left(x^2+4x+8\right)\)

Ta có: xy\(\perp\)AB

x'y'\(\perp\)AB

Do đó: xy//x'y'

\(\left\{{}\begin{matrix}x+2y=1+3\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\7y=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2=4\\y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=4-2=2\\y=1\end{matrix}\right.\)

Vậy: ...

\(\left\{{}\begin{matrix}x+2y=1+3\\2x-3y=1\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x+4y-\left(2x-3y\right)=8-1\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x+4y-2x+3y=7\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}2x+4y=8\\\left(2x-2x\right)+\left(4y+3y\right)=7\end{matrix}\right.\)

⇒  \(\left\{{}\begin{matrix}2x+4y=8\\0+7y=7\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}2x+4y=8\\y=1\end{matrix}\right.\)

Thay y = 1 vào biểu thức 2\(x\) + 4y = 8 ta có: 2\(x\) + 4.1 = 8 

⇒ 2\(x\) + 4 = 8 ⇒ 2\(x\) = 4 ⇒ \(x\) = 4: 2 ⇒ \(x\) = 2

Vậy \(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

Bài 3:

Ta có: \(\dfrac{1}{5^2}< \dfrac{1}{4\cdot5};\dfrac{1}{6^2}< \dfrac{1}{5\cdot6};...;\dfrac{1}{100^2}< \dfrac{1}{99\cdot100}\)

\(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+...+\dfrac{1}{99\cdot100}\\=> \dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ =>\dfrac{1}{5^2}+\dfrac{1}{6^2}+..+\dfrac{1}{100^2}< \dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\left(1\right)\)

Ta có: \(\dfrac{1}{5^2}>\dfrac{1}{5\cdot6};\dfrac{1}{6^2}>\dfrac{1}{6\cdot7};...;\dfrac{1}{100^2}>\dfrac{1}{100\cdot101}\)

\(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}>\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+..+\dfrac{1}{100\cdot101}\\ =>\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}>\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{100}-\dfrac{1}{101}\\ =>\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}>\dfrac{1}{5}-\dfrac{1}{101}=\dfrac{96}{505}>\dfrac{96}{576}=\dfrac{1}{6}\left(2\right)\)

Từ (1) và (2) => \(\dfrac{1}{6}< \dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4}\)

a) Ta có: \(\widehat{cNb}+\widehat{MNb}=180^{\circ}\) (hai góc kề bù)

\(\Rightarrow\widehat{MNb}=180^{\circ}-\widehat{cNb}=180^{\circ}-55^{\circ}=125^{\circ}\)

b) Ta có: \(\widehat{MNb}=\widehat{aMN}\left(=125^{\circ}\right)\)

Mà hai góc này đều nằm ở vị trí so le trong

Nên \(Ma//Nb\)