Cho lưới ô vuông 6x6. Người ta điền vào mỗi ô vuông một trong các số -1; 0; 1. Xét tổng các số được tính theo hàng, theo cột, theo từng đường chéo. chứng minh rằng luôn tồn tại hai tổng có giá trị bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.


C = \(x^2\) - 12 \(x\) + 34
C = (\(x^2\) - 12\(x\) + 36) - 2
C = (\(x\) - 6)2 - 2
Vì (\(x\) - 6)2 ≥ 0 ⇒ ( \(x\) - 6)2 - 2 ≥ -2
C(min) = - 2 ⇔ \(x\) - 6 = 0 ⇔ \(x\) = 6
Vậy giá trị nhỏ nhất của biểu thức là - 2 xảy ra khi \(x\) = 6
C = - 12 + 34
C = ( - 12 + 36) - 2
C = ( - 6)2 - 2
Vì ( - 6)2 ≥ 0 ⇒ ( - 6)2 - 2 ≥ -2
C(min) = - 2 ⇔ - 6 = 0 ⇔ = 6
Vậy giá trị nhỏ nhất của biểu thức là - 2 diễn ra khi = 6

A = - 4\(x\)2 + 5\(x\) - 3
A = -( 4\(x^2\) - 5\(x\) + \(\dfrac{25}{16}\)) - \(\dfrac{23}{16}\)
A = -( 2\(x\) - \(\dfrac{5}{4}\))2 - \(\dfrac{23}{16}\)
Vì ( 2\(x\) - \(\dfrac{5}{4}\))2 ≥ 0; ⇒ - ( 2\(x\) - \(\dfrac{5}{4}\))2 ≤ 0 ⇒ -( 2 \(x\) - \(\dfrac{5}{4}\))2 - \(\dfrac{23}{16}\) ≤ - \(\dfrac{23}{16}\)
A(max) = - \(\dfrac{23}{16}\) ⇔ 2\(x\) - \(\dfrac{5}{4}\) = 0 ⇔ \(x\) = \(\dfrac{5}{4}\): 2 = \(\dfrac{5}{8}\)
Kết luận giá trị lớn nhất của biểu thức là - \(\dfrac{23}{16}\) xáy ra khi \(x\) = \(\dfrac{5}{8}\)

Lời giải:
Đặt $x-y=a; y-z=b, z-x=c$
$\Rightarrow a+b+c=0$
Theo đề ta có:
$(x-y)^2+(y-z)^2+(z-x)^2=[(z-x)-(x-y)]^2+[(x-y)-(y-z)]^2+[(y-z)-(z-x)]^2$
$\Leftrightarrow a^2+b^2+c^2=(c-a)^2+(a-b)^2+(b-c)^2$
$\Leftrightarrow a^2+b^2+c^2=2a^2+2b^2+2c^2-2(ab+bc+ac)$
$\Leftrightarrow 2(a^2+b^2+c^2)=a^2+b^2+c^2+2(ab+bc+ac)$
$\Leftrightarrow 2(a^2+b^2+c^2)=(a+b+c)^2=0$
$\Rightarrow a^2+b^2+c^2=0$
$\Rightarrow a=b=c=0$
$\Leftrightarrow x-y=y-z=z-x=0$
$\Leftrightarrow x=y=z$

`A = -25x^2 +30x -2 = -(25x^2 -30x +2)`
`= -[(5x)^2 - 2*5x*3 +3^2 +2-3^2]`
`=-[(5x-3)^2 -7] = 7-(5x-3)^2`
Do `-(5x-3)^2 <= 0 AA x`
`=> 7- (5x-3)^2 <0 AA x `
hay `A<0 AA x (đpcm)`
từ đã có gì đó hơi sai sai
\(7-\left(5x-3\right)^2=-\left(5x-3\right)^2+7\) mà=)))
sao nó lại nhỏ hơn không nhỉ=)))

`B =9x^2 +6x = (3x)^2 + 2*3x*1 +1 -1)`
`=(3x +1)^2 -1`
Do `(3x+1)^2 >=0 AA x`
`=> (3x+1)^2 -1 >=-1 AA x`
hay `B>=-1`
Dấu ''='' xảy ra khi và chỉ khi `3x+1=0 =>x =-1/3`
Vậy GTNN của `B=-1` khi `x=-1/3`
B = 9\(x^2\) + 6\(x\)
B = 9\(x^2\) + 6\(x\) + 1 - 1
B = (3\(x\) + 1)2 - 1
Vì (3\(x\) + 1)2 ≥ 0 ⇒ (3\(x\) + 1)2 - 1 ≥ -1
B(min) = -1⇔ \(x\) = - \(\dfrac{1}{3}\)
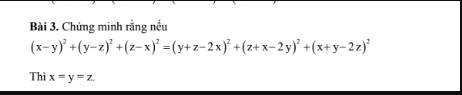
Kí hiệu \(S\) là tổng tất cả các số trên cùng 1 hàng, cột hay đường chéo. Dễ dàng kiểm chứng được \(-6\le S\le6\). Ta thấy từ \(-6\) đến \(6\) có tất cả là 13 số nguyên. Nói cách khác, sẽ có tất cả 13 giá trị khác nhau mà \(S\) có thể đạt được. Do trên bảng 6x6 có 6 cột, 6 hàng, 2 đường chéo ứng với 14 tổng S nên theo nguyên lí Dirichlet, sẽ tồn tại 2 tổng S mang cùng 1 giá trị, đây là đpcm.