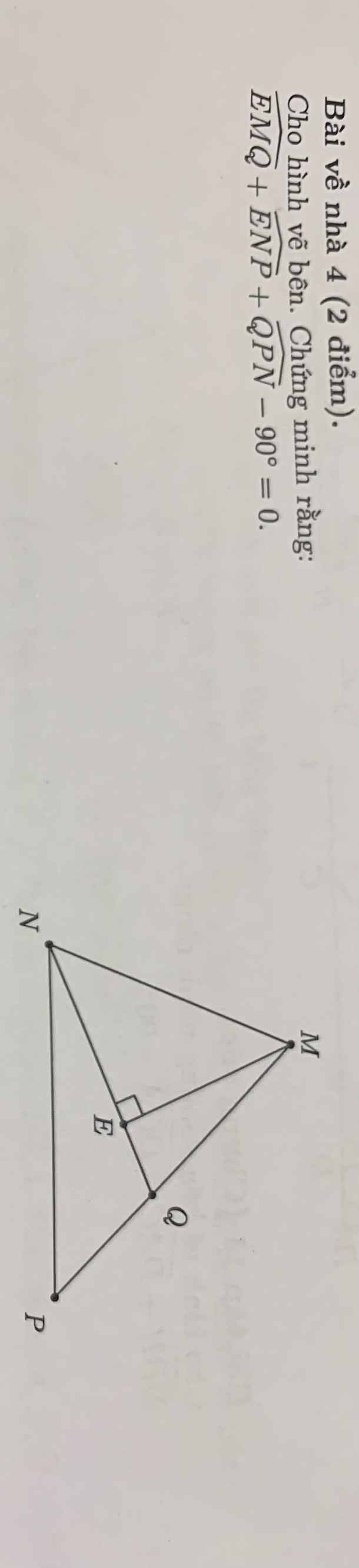Bài 1:

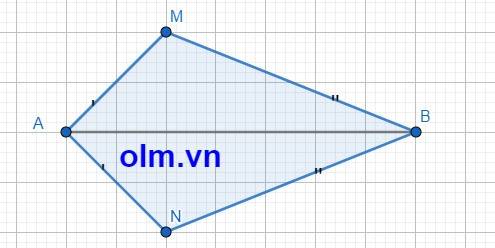
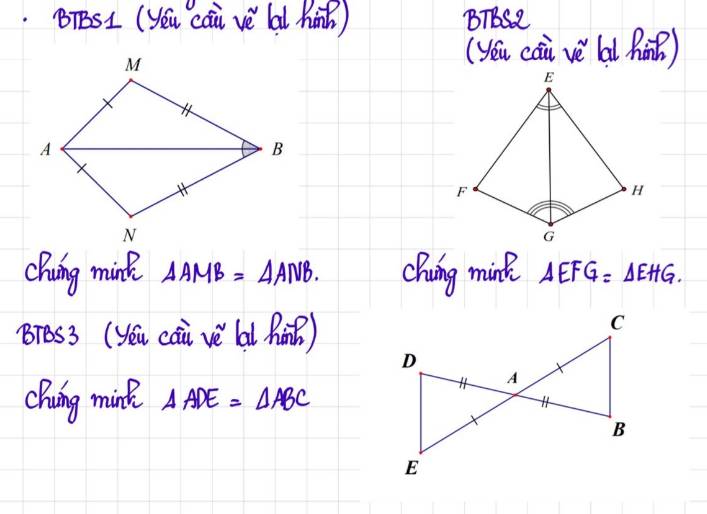
Xét tam giác AMB và tam giác ANB có:

            AM = AN

           BM = BN 

            AB chung

⇒ \(\Delta\)AMB  = \(\Delta\)ANB  (c-c-c) (đpcm)

Bài 2:

Xét tam giác EFG và tam giác EHG có:

 GE chung

Góc FEG = Góc HEG 

góc FGE = góc EGH 

⇒ \(\Delta\)EFG = \(\Delta\)EGH (g- c -g)

Do tam giác MQE vuông tại E \(\Rightarrow\widehat{EMQ}+\widehat{EQM}=90^0\) (1)

Mà \(\widehat{EQM}\) là góc ngoài của tam giác NPQ, theo tính chất góc ngoài của tam giác:

\(\widehat{EQM}=\widehat{ENP}+\widehat{QPN}\) (2)

\(\left(1\right);\left(2\right)\Rightarrow\widehat{EMQ}+\widehat{ENP}+\widehat{QPN}=90^0\)

\(\Rightarrow\widehat{EMQ}+\widehat{ENP}+\widehat{QPN}-90^0=0\)

Lời giải:
a. Vì $x,y$ là 2 đại tượng tỉ lệ nghịch nên $xy=k$ không đổi với $k$ là hệ số tỉ lệ.

Thay $x=-3; y=-7$ thì: $k=xy=(-3)(-7)=21$

b. $xy=21\Rightarrow x=\frac{21}{y}$

c. Khi $x=9$ thì: $y=\frac{21}{x}=\frac{21}{9}=\frac{7}{3}$
d. Khi $y=-6$ thì $x=\frac{21}{y}=\frac{21}{-6}=\frac{-7}{2}$

máy cái vuông vuông kia là j hả bn

 Là kí hiệu tâm giác á

Một người thợ sẽ xây xong một bức tường đó trong:

\(9\times4=36\left(ngày\right)\)

Sáu người thợ sẽ xây xong một bức tường đó trong:

\(36:6=6\left(ngày\right)\)

Đáp số: \(6\) \(ngày\)

Muốn biết bốn người thợ đó xây xong bức tường trong bao nhiêu ngày thì phải có số liệu chứ bạn. Bạn bổ sung đề nhé.

nhìn hình ta thấy=))

A B C N P G

Ta có

\(BG=\dfrac{2}{3}BN\) (t/c đường trung tuyến) \(\Rightarrow BN=\dfrac{3}{2}BG\)

\(CG=\dfrac{2}{3}CP\) (t/c đường trung tuyến) \(\Rightarrow CP=\dfrac{3}{2}CG\)

\(\Rightarrow BN+CP=\dfrac{3}{2}\left(BG+CG\right)\) (1)

Xét tg BCG có

\(BG+CG>BC\) (trong tg tổng 2 cạnh lớn hơn cạnh còn lại)

\(\Rightarrow\dfrac{3}{2}\left(BG+CG\right)>\dfrac{3}{2}BC\) (2)

Từ (1) và (2) \(\Rightarrow BN+CP>\dfrac{3}{2}BC\left(dpcm\right)\)

Đặt \(\dfrac{a}{3}=\dfrac{b}{5}=k(k\in\mathbb{N})\)

\(\Rightarrow a=3k;b=5k\left(1\right)\)

Thay \(\left(1\right)\) vào \(a^2+b^2=136\), ta được:

\(\left(3k\right)^2+\left(5k\right)^2=136\)

\(\Rightarrow9k^2+25k^2=136\)

\(\Rightarrow34k^2=136\)

\(\Rightarrow k^2=136:34=4\)

\(\Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\)

Mà \(k\in\mathbb{N}\) nên \(k=2\)

Khi đó: \(\left\{{}\begin{matrix}a=2\cdot3=6\\b=2\cdot5=10\end{matrix}\right.\left(tm\right)\)

Vậy \(\left(a;b\right)=\left(6;10\right)\).