1. Tìm nghiệm nguyên dương của phương trinh x2-2y2-xy –x +5y-6=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


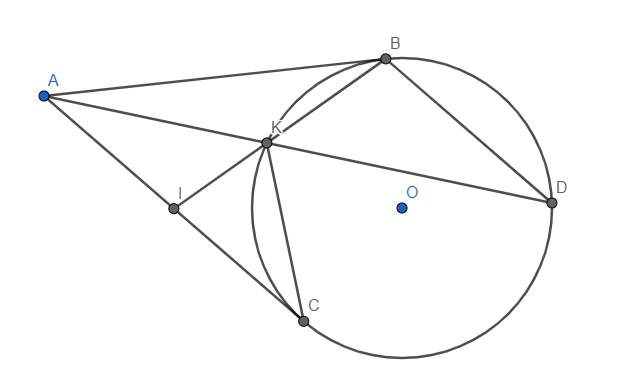
b) Do BD//AC nên \(\widehat{KAI}=\widehat{KDB}\) (2 góc so le trong)
Lại có \(\widehat{ABI}=\widehat{ABK}=\widehat{BDK}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BK.
\(\Rightarrow\widehat{KAI}=\widehat{KBA}\)
c) I là trung điểm AC chứ không phải BC nhé.
Xét tam giác IAK và IBA, ta có:
\(\widehat{AIB}\) chung, \(\widehat{IAK}=\widehat{IBA}\left(cmt\right)\)
\(\Rightarrow\Delta IAK\sim\Delta IBA\left(g.g\right)\)
\(\Rightarrow\dfrac{IA}{IB}=\dfrac{IK}{IA}\)
\(\Rightarrow IA^2=IB.IK\)
\(\Rightarrow IA=IC\) (vì theo câu a, \(IC^2=IB.IK\))
\(\Rightarrow\) I là trung điểm AC.
d) CK vuông góc với đường nào trong đề bài chưa nói nhé.

a: Xét tứ giác MIKC có \(\widehat{MIC}=\widehat{MKC}=90^0\)
nên MIKC là tứ giác nội tiếp
Xét tứ giác MIAH có \(\widehat{MIA}+\widehat{MHA}=90^0+90^0=180^0\)
nên MIAH là tứ giác nội tiếp
Xét tứ giác MKBH có \(\widehat{MKB}+\widehat{MHB}=90^0+90^0=180^0\)
nên MKBH là tứ giác nội tiếp
b: Ta có: MIKC là tứ giác nội tiếp
=>\(\widehat{MIK}+\widehat{MCK}=180^0\)
=>\(\widehat{MIK}=180^0-\widehat{MCB}\)
Ta có: HAIM là tứ giác nội tiếp
=>\(\widehat{MIH}=\widehat{MAH}\)
mà \(\widehat{MAH}=\widehat{MCB}\left(=180^0-\widehat{MAB}\right)\)
nên \(\widehat{MIH}=\widehat{MCB}\)
=>\(\widehat{MIH}+\widehat{MIK}=180^0\)
=>K,I,H thẳng hàng


\(\sqrt{3+2\sqrt{2}}-\sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\)
\(=\sqrt{2+2\sqrt{2}+1}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)
\(=\sqrt{\left(\sqrt{2}\right)^2+2\sqrt{2}\cdot1+1^2}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}\right)^2-1^2}}\)
\(=\sqrt{2}+1-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{2-1}}\)
\(=\sqrt{2}+1-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{1}}\)
\(=\sqrt{2}+1-\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=\sqrt{2}+1-\left(\sqrt{2}-1\right)\)
\(=\sqrt{2}+1-\sqrt{2}+1=2\)

Xét 2024 số:
\(a_1=2024\)
\(a_2=20242024\)
\(a_3=202420242024\)
...
\(a_{2024}=20242024...2024\) (2024 lần cụm "2024")
Một số khi chia cho 2023 thì có 2023 số dư phân biệt là 0, 1, 2,..., 2023
\(\Rightarrow\) Theo nguyên lí Dirichlet tồn tại 2 số \(a_i,a_j\left(i\ne j,1\le i< j\le2024\right)\) trong số 2024 số kể trên có cùng số dư khi chia cho 2023.
\(\Rightarrow a_j-a_i⋮2023\)
\(\Rightarrow20242024...2024-20242024...2024⋮2023\)
(\(j\) cụm "2024) (\(i\) cụm "2024)
\(\Rightarrow20242024...2024000...00⋮2023\)
(\(j-i\) cụm "2024" và \(i\) chữ số 0)
\(\Rightarrow20242024...2024.10^i⋮2023\) (*)
Nhưng vì \(10^i=2^i.5^i\) và \(2023=7.17^2\) nên \(ƯCLN\left(10^i,2023\right)=1\)
Từ đó (*) suy ra \(20242024...2024⋮2023\)
(\(j-i\) cụm 2024)
Ta có đpcm.

Tham khảo:
Gọi: số tiền loại 50000 đ là x ; số tiền loại 500000 đ là y
Ta có: x + y = 15 (1)
50000x + 200000y -30000= 1320000 (1)
Giải hai phương trình trên :
{x=11
y=4

a/
E và F bình đẳng nhau nên tôi chỉ c/m ME là tiếp tuyến với đường tròn đường kính AH. Còn c/m MF là tiếp tuyến làm tương tự bạn tự c/m nhé
Gọi I là tâm đường tròng đường kính AH => IA=IH
Gọi D là giao của AH với BC
Xét tg ABC có \(AH\perp BC\) (trong tg 3 đường cao đồng quy)
\(\Rightarrow AD\perp BC\)
Xét tg vuông ADC và tg vuông BEC có
\(\widehat{DAC}=\widehat{EBC}\) (cùng phụ với \(\widehat{C}\) ) (1)
Xét tg vuông AHE có
\(IA=IH\Rightarrow IE=IA=IH=\dfrac{AH}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
\(\Rightarrow E\in\left(I\right)\) và tg AIE cân tại I
\(\Rightarrow\widehat{DAC}=\widehat{AEI}\) (góc ở đáy tg cân) (2)
Xét tg vuông BEC có
\(MB=MC\left(gt\right)\Rightarrow ME=MB=MC=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg BME cân tại M
\(\Rightarrow\widehat{EBC}=\widehat{BEM}\) (góc ở đáy tg cân) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{AEI}=\widehat{BEM}\)
Mà \(\widehat{AEI}+\widehat{BEI}=\widehat{AEB}=90^o\)
\(\Rightarrow\widehat{BEM}+\widehat{BEI}=\widehat{MEI}=90^o\Rightarrow ME\perp IE\) => ME là tiếp tuyến với đường tròn đường kính AH
b/
Xét tg MEK và tg MAE có
\(\widehat{AME}\) chung
Ta có
\(sđ\widehat{MEK}=\dfrac{1}{2}sđcungEK\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MAE}=\dfrac{1}{2}sđcungEK\) (góc nội tiếp (O))
\(\Rightarrow\widehat{MEK}=\widehat{MAE}\)
=> tg MEK đồng dạng với tg MAE (g.g.g)
\(\Rightarrow\dfrac{ME}{MA}=\dfrac{MK}{ME}\Rightarrow MK.MA=ME^2\)

\(P=\left(a^2+\dfrac{1}{16}+\dfrac{1}{16}+\dfrac{1}{16}\right)+\left(b^2+\dfrac{1}{16}+\dfrac{1}{16}+\dfrac{1}{16}\right)-\dfrac{3}{8}\)
\(P\ge4\sqrt[4]{\dfrac{a^2}{16^3}}+4\sqrt[4]{\dfrac{b^2}{16^3}}-\dfrac{3}{8}=\dfrac{1}{2}\left(\sqrt{a}+\sqrt{b}\right)-\dfrac{3}{8}=\dfrac{1}{8}\)
\(P_{min}=\dfrac{1}{8}\) khi \(a=b=\dfrac{1}{4}\)
Do \(\left\{{}\begin{matrix}a;b\ge0\\\sqrt{a}+\sqrt{b}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}0\le a\le1\\0\le b\le1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{a}\ge a^2\\\sqrt{b}\ge b^2\end{matrix}\right.\)
\(\Rightarrow a^2+b^2\le\sqrt{a}+\sqrt{b}=1\)
\(P_{max}=1\) khi \(\left(a;b\right)=\left(1;0\right);\left(0;1\right)\)

Do (d) đi qua A nên:
\(0.m+n=-1\Rightarrow n=-1\)
\(\Rightarrow y=mx-1\)
Pt hoành độ giao điểm (P) và (d):
\(\dfrac{1}{2}x^2=mx-1\Leftrightarrow x^2-2mx+2=0\) (1)
(d) tiếp xúc (P) khi và chỉ khi (1) có nghiệm kép
\(\Rightarrow\Delta'=m^2-2=0\Rightarrow m=\pm\sqrt{2}\)
- Với \(m=\sqrt{2}\Rightarrow x=-\dfrac{b}{2a}=\sqrt{2}\Rightarrow y=\dfrac{1}{2}x^2=1\)
Tọa độ tiếp điểm là \(\left(\sqrt{2};1\right)\)
- Với \(m=-\sqrt{2}\Rightarrow x=-\dfrac{b}{2a}=-\sqrt{2}\Rightarrow y=1\)
Tọa độ tiếp điểm là \(\left(-\sqrt{2};1\right)\)

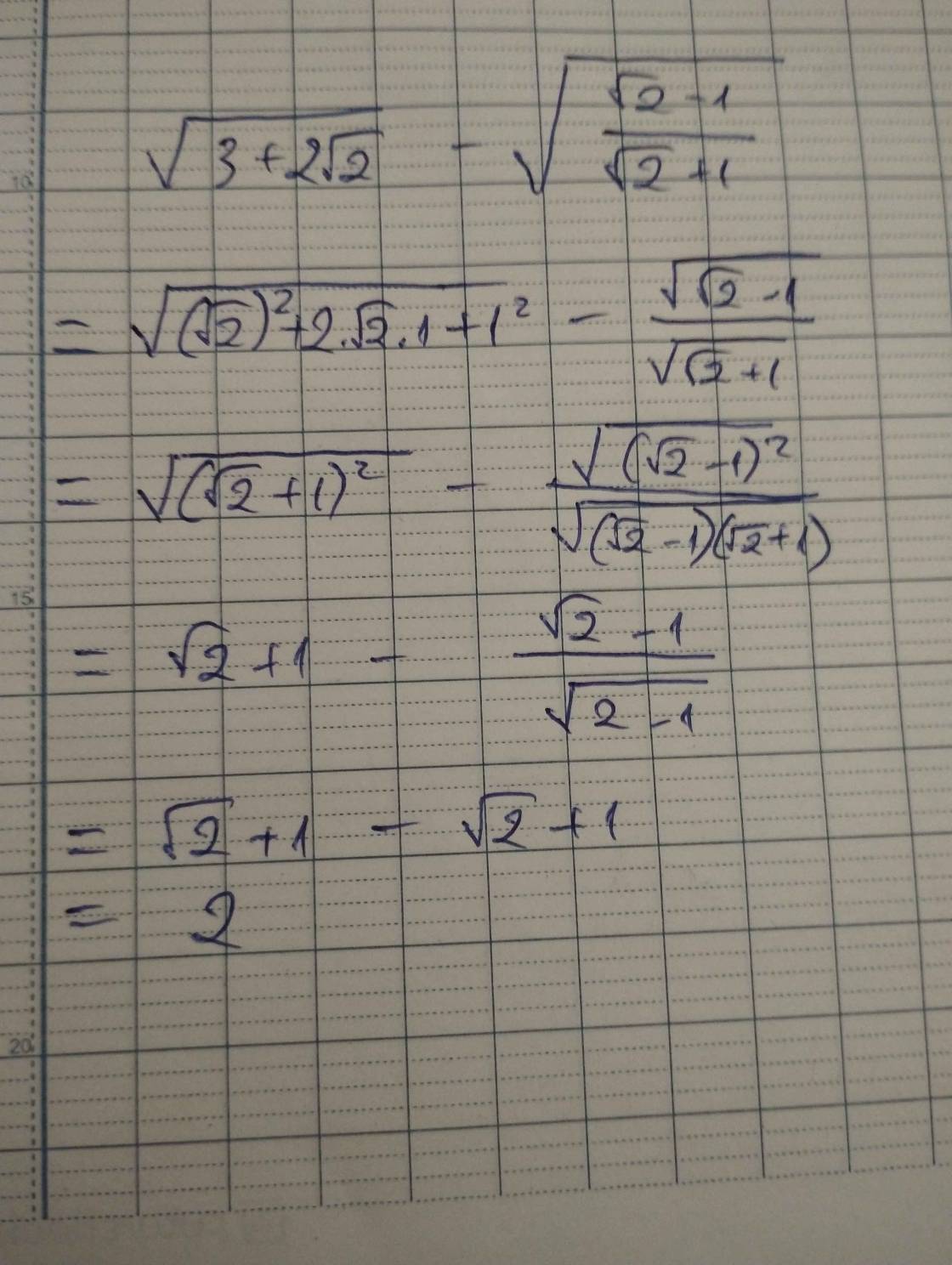
pt đã cho \(\Leftrightarrow x^2-\left(y+1\right)x-2y^2+5y-6=0\) (*)
Ta tính được \(\Delta=9y^2-18y+25>0\) với mọi y.
Để (*) có nghiệm nguyên thì \(9y^2-18y+25\) là số chính phương
\(\Leftrightarrow9y^2-18y+25=z^2\left(z\inℕ,z\ge4\right)\)
\(\Leftrightarrow\left(3y-3\right)^2+16=z^2\)
\(\Leftrightarrow\left(z+3y-3\right)\left(z-3y+3\right)=16\)
Ta có bảng sau:
Vậy \(y=1\) \(\Rightarrow x^2-2x-3=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
Vậy pt đã cho có các nghiệm nguyên là \(\left(-1;1\right)\) và \(\left(3;1\right)\)