Áp dụng BĐT \(x^2+y^2\ge\dfrac{1}{2}\left(x+y\right)^2\)

\(\Rightarrow1\ge\dfrac{1}{2}\left(x+y\right)^2\)

\(\Rightarrow2\ge\left(x+y\right)^2\)

\(\Rightarrow-\sqrt{2}\le x+y\le\sqrt{2}\)

Đầu tiên ta sẽ chứng minh BDT phụ \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\)

Thật vậy, ta có BDT luôn đúng: \(\left(a-b\right)^2\ge0\) \(\Leftrightarrow a^2+b^2\ge2ab\) \(\Leftrightarrow2a^2+2b^2\ge a^2+2ab+b^2\) \(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)

Vậy BDT phụ được chứng minh, dấu "=" xảy ra khi \(a=b\)

Áp dụng BĐT, ta được \(\left(x+y\right)^2\le2\left(x^2+y^2\right)=2\) (vì \(x^2+y^2=1\))

Từ đó \(-\sqrt{2}\le x+y\le\sqrt{2}\)

Dấu "=" xảy ra khi \(x=y\), kết hợp với giả thiết \(x^2+y^2=1\) thì ta có \(x=y=\dfrac{\sqrt{2}}{2}\)

\(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-5-x^2+6x\)

Ta có:

\(\sqrt{3x^2-18x+28}=\sqrt{3\left(x^2-6x+9\right)+1}=\sqrt{3\left(x-3\right)^2+1}\ge1\forall x\)

\(\sqrt{4x^2-24x+45}=\sqrt{4\left(x^2-6x+9\right)+9}=\sqrt{4\left(x-3\right)^3+9}\ge3x\forall\)

\(\Rightarrow VT\ge4\forall x\)\(\left(1\right)\)

Ta có:

\(VP=-5-x^2+6x=-\left(x^2-6x+9\right)+4=-\left(x-3\right)^2+4\le4\forall x\left(2\right)\)

Từ (1) và (2)

\(\Rightarrow\) Dấu "=" xảy ra \(\Leftrightarrow x=3\)

\(=\dfrac{\left(\sqrt{a}-2\right)^2-\left(\sqrt{a}+2\right)^2}{a-4}.\dfrac{a-4}{\sqrt{a}}=\)

\(=\dfrac{a-4\sqrt{a}+4-a-4\sqrt{a}-4}{\sqrt{a}}=-8\)

\(\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}\)

\(=\sqrt{13+30\sqrt{2+\sqrt{9+2\sqrt{8}}}}\)

\(=\sqrt{13+30\sqrt{2+\sqrt{\left(\sqrt{8}+1\right)^2}}}\)

\(=\sqrt{13+30\sqrt{2+2\sqrt{2}+1}}\)

\(=\sqrt{13+30\sqrt{\left(\sqrt{2}+1\right)^2}}\)

\(=\sqrt{13+30.\left(\sqrt{2}+1\right)}\)

\(=\sqrt{43+30\sqrt{2}}\)

\(=\sqrt{43+30\sqrt{2}}\)

còn lại tự làm nốt

a) Như mình đã nói với bạn thì áp dụng định lý cos trong tam giác ABC, ta có \(BC=\sqrt{AB^2+AC^2-2AB.AC.cos\widehat{BAC}}\) \(=\sqrt{8^2+8^2-2.8.8.cos34}\) \(\approx4,678\left(cm\right)\)

b) Áp dụng định lý sin cho tam giác ACD, ta được \(\dfrac{AC}{sinD}=\dfrac{CD}{sin\widehat{CAD}}\) \(\Rightarrow sinD=\dfrac{AC.sin\widehat{CAD}}{CD}=\dfrac{8.sin42^o}{6}\) \(\Rightarrow\widehat{D}\approx63,148^o\)

c) Gọi BH là khoảng cách từ B đến AD .Khi đó tam giác ABH vuông tại H nên \(BH=AB.sin\widehat{BAH}\)

Dễ thấy \(\widehat{BAH}=\widehat{BAC}+\widehat{CAD}=34^o+42^o=76^o\) nên \(BH=8.sin76^o\approx7,762\left(cm\right)\)

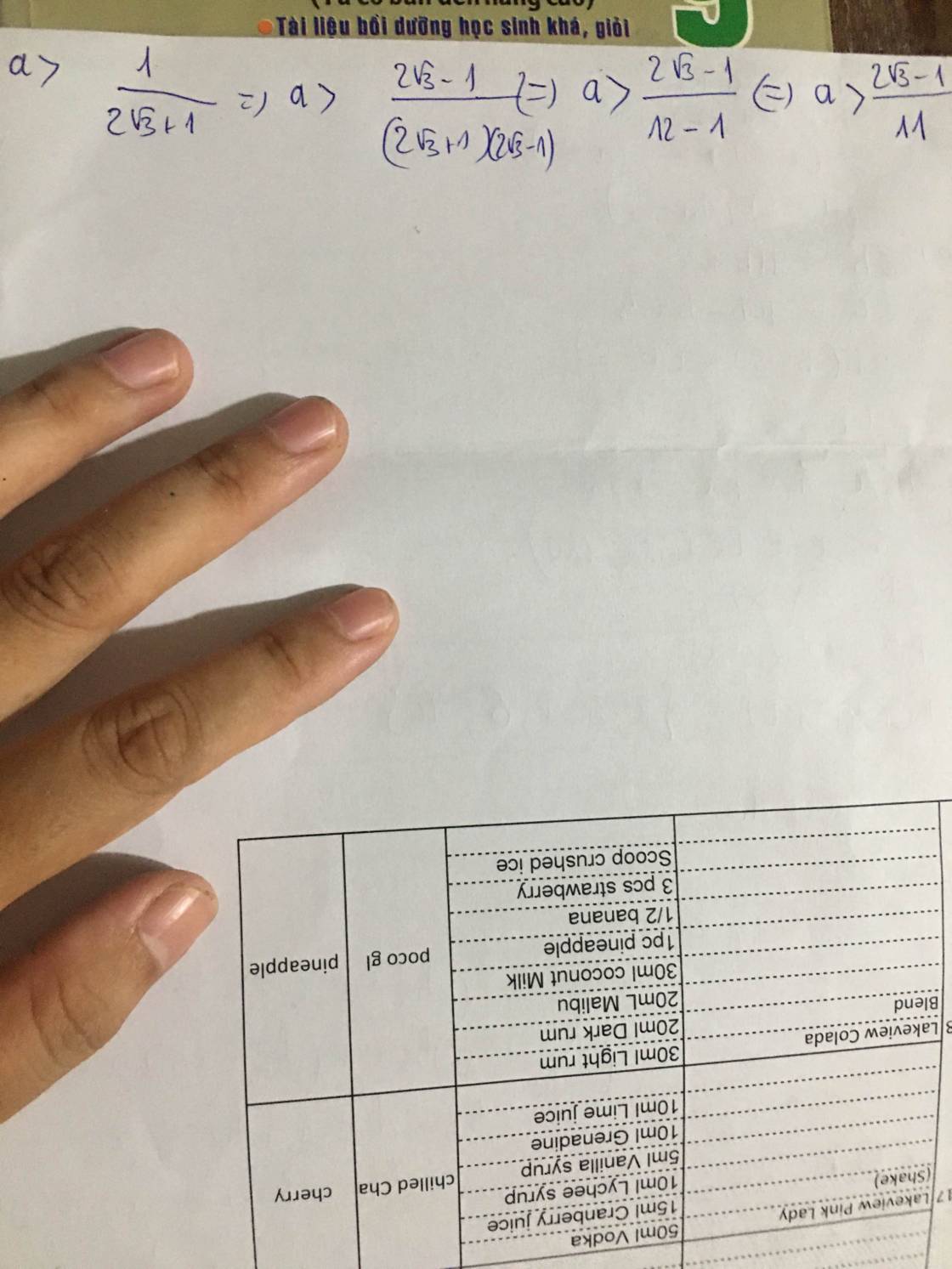
\(\dfrac{1}{2\sqrt{3}+1}=\dfrac{2\sqrt{3}-1}{\left(2\sqrt{3}+1\right)\left(2\sqrt{3}-1\right)}=\dfrac{2\sqrt{3}-1}{4.3-1}=\dfrac{2\sqrt{3}-1}{11}\)