 help voii a
help voii a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{4^5\cdot9^4-2\cdot6^9}{2^{10}\cdot3^8+6^8\cdot20}\\ =\dfrac{\left(2^2\right)^5\cdot\left(3^2\right)^4-2\cdot2^9\cdot3^9}{2^{10}\cdot3^8+2^8\cdot3^8\cdot20}\\ =\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^8\cdot3^8\cdot2^2\cdot5}\\ =\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^{10}\cdot3^8\cdot5}\\ =\dfrac{2^{10}\cdot3^8\cdot\left(1-3\right)}{2^{10}\cdot3^8\cdot\left(1+5\right)}\\ =\dfrac{-2}{6}\\ =-\dfrac{1}{3}\)

\(B=4\cdot2^7:\left(3^{11}\cdot\dfrac{1}{9}\right)\\ =4\cdot2^7:\left(3^{11}\cdot\dfrac{1}{3^2}\right)\\ =4\cdot2^7:\dfrac{3^{11}}{3^2}\\ =4\cdot2^7:3^9\\ =\dfrac{2^2\cdot2^7}{3^9}\\ =\dfrac{2^9}{3^9}\\ =\left(\dfrac{2}{3}\right)^9\)

\(b)\left\{{}\begin{matrix}x-\dfrac{y}{2}=\dfrac{1}{2}\\\dfrac{x}{3}-2y=-\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=1\\x-6y=-5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x-y=1\\2x-12y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11y=11\\2x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\2x=1+1=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=1\\x=1\end{matrix}\right.\)
\(c)\left\{{}\begin{matrix}5x-0,7y=1\\-10x+1,4y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-0,7y=1\\-5x+0,7y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-0,7y=1\\-5x+0,7y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-0,7y=1\\5x-0,7y=1\end{matrix}\right.\)
=> Hpt vô số nghiệm
Cho $x, \, y$ là hai số thực lớn hơn $\sqrt{2}$. Chứng minh rằng $x^4-x^3y+x^2y^2-xy^3+y^4>x^2+y^2$.


Xét \(f\left(x\right)=VT=x^2+y^2+xy-3x-3y+3\)
\(=x^2+\left(y-3\right)x+y^2-3y+3\)
Có \(\Delta=\left(y-3\right)^2-4\left(y^2-3y+3\right)\)
\(=y^2-6y+9-4y^2+12y-12\)
\(=-3y^2+6y-3\)
\(=-3\left(y-1\right)^2\le0\) với mọi \(y\inℝ\)
Mà \(f\left(x\right)\) có hệ số cao nhất bằng \(1>0\) nên từ đây có \(VT=f\left(x\right)\ge0\)
Dấu "=" xảy ra khi \(y=1\). Khi đó \(\Delta=0\) nên pt \(f\left(x\right)=0\) có nghiệm kép \(\Leftrightarrow\) \(x=\dfrac{-\left(y-3\right)}{2}=1\).
Ta có đpcm.


\(\left(2x-1\right)^{50}=2x-1\\ =>\left(2x-1\right)^{50}-\left(2x-1\right)=0\\ =>\left(2x-1\right)\left[\left(2x-1\right)^{49}-1\right]=0\)
TH1:
\(2x-1\\ =>2x=1\\ =>x=\dfrac{1}{2}\)
TH2:
\(\left(2x-1\right)^{49}-1=0\\=>\left(2x-1\right)^{49}=1\\ =>\left(2x-1\right)^{49}=1^{49}\\ =>2x-1=1\\ =>2x=1+1=2\\ =>x=\dfrac{2}{2}\\ =>x=1\)
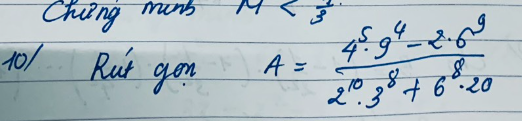

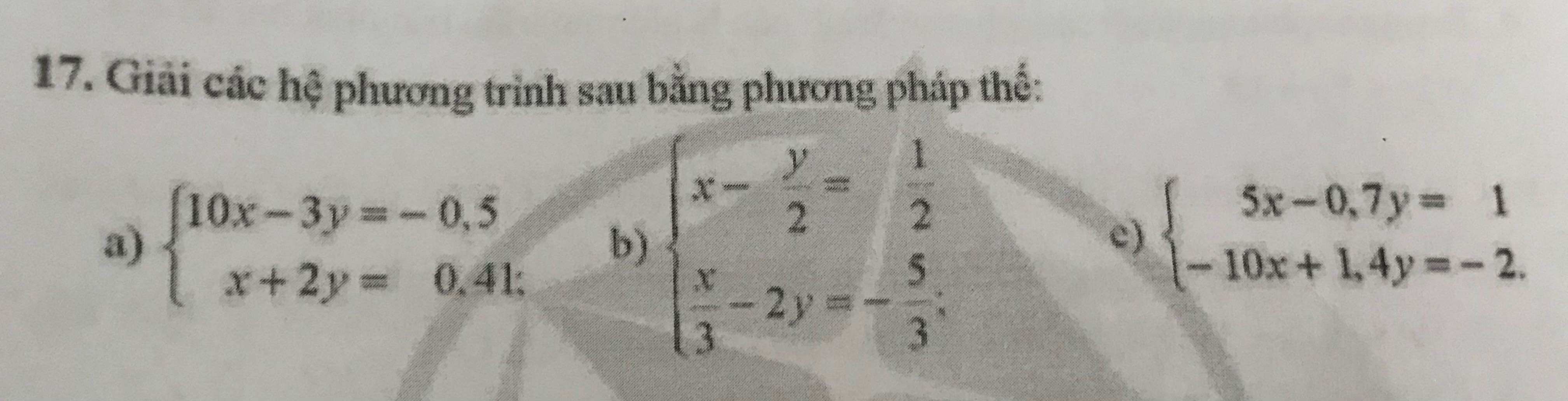

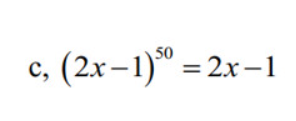
Giải:
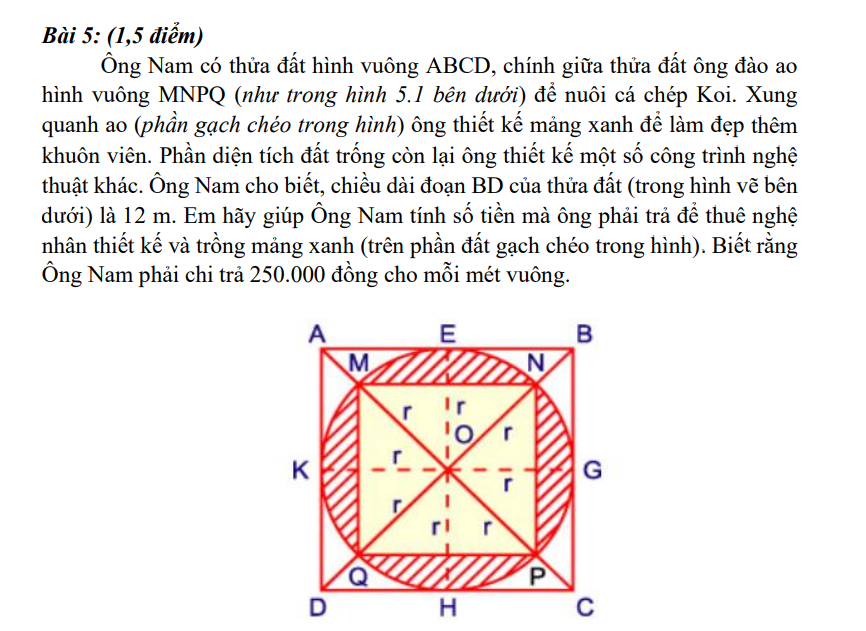
Diện tích của hình vuông ABCD là: 12 x 12 : 2 = 72 (m2)
Diện tích của hình tròn tâm O bán kính OK là:
KG.EH.3,14 : 4 = \(\dfrac{1}{4}\)KG.EH = \(\dfrac{3,14}{4}\)SABCD = 72 x \(\dfrac{3,14}{4}\) = 56,52 (m2)
⇒ MP.QN.3,14:4 = 56,52
⇒ MP.QN = 56,52 x 4 : 3,14 = 72
Diện tích hình vuông MNPQ là:
MP.QN : 2 = 72: 2 = 36 (m2)
Diện tích phần gạch chéo là:
56,52 - 36 = 20,52 (m2)
Số tiền ông Nam phải chi trả cho nghệ nhân trang trí phần diện tích gạch chéo là:
250 000 x 20,52 = 5 130 000 (đồng)
Kết luận:...