b) \(\left(3x-9\right)\times12=36\) 

               \(3x-9=36\div12=3\) 

                       \(3x=3+9=12\) 

                          \(x=12\div3\) 

                          \(x=4\) 

c) \(\left(x+1\right)+\left(x+4\right)+...+\left(x+100\right)=1751\) 

            \(x+1+x+4+....+x+100=1751\) 

   \(\left(x+x+...+x\right)+\left(1+4+...+100\right)=1751\) 

Số số hạng là \(\left(100-1\right)\div3+1=34\) ( số hạng )

=> Ta có 34 số hạng x

Tổng là \(\left(100+1\right)\times34\div2=1717\) 

=> \(x\times34+1717=1751\) 

                 \(x\times34=1751-1717\) 

                  \(x\times34=34\) 

                            \(x=34\div34\) 

                            \(x=1\)

b; (3\(x\) - 9).12 = 36

     3\(x\) - 9       = 36: 12

     3\(x\) - 9      = 3

     3\(x\)            = 3 + 9

     3\(x\)            = 12

       \(x\)            = 12: 3

       \(x\)             = 4

c, (\(x\) + 1) + (\(x\) + 4)+...+ (\(x\) + 100) = 1751

    Dãy số trên là dãy số cách đều với khoảng cách là:

                   \(x\) + 4 - \(x\) - 1 = 3

Số số hạng của dãy số trên là:( \(x\) + 100 - \(x\) - 1):3 = 34

 Ta có: (\(x\) + 100 + \(x\) + 1)\(\times\) 34 : 2 = 1751

               (2\(x\) + 101) \(\times\) 17 = 1751

                2\(x\) + 101  = 1751 : 17

                2\(x\)  + 101 = 103

                 2\(x\)            = 103 - 101

                2\(x\)            = 2

                  \(x\)           = 1 

giúp với trí ơi

giúp nốt trí ui

mu là mũ nha giúp tui vứi

a) \(82^2-18^2=\left(82-18\right)\left(82+18\right)=64.100=6400\)

b) \(26^2+52.24+24^2=26^2+2.26.24+24^2=\left(26+24\right)^2=50^2=2500\)

c) \(\dfrac{93^3+78^3}{171}-93.78=\dfrac{\left(93+78\right)\left(93^2-93.78+73^2\right)}{171}-93.78\)

\(=\dfrac{171\left(93^2-93.78+73^2\right)}{171}-93.78\)

\(=93^2-93.78+73^2-93.78\)

\(=93^2-2.93.78+73^2=\left(93-73\right)^2=20^2=400\)

a/

\(x^3-4x^2-\left(x-4\right)=0\)

\(\Leftrightarrow x^2\left(x-4\right)-\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x^2-1\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x-1=0\\x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=1\\x=-1\end{matrix}\right.\)

b/

\(x^5-9x=0\)

\(\Leftrightarrow x\left(x^4-9\right)=x\left(x^2-3\right)\left(x^2+3\right)=0\)

\(\Leftrightarrow x\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\sqrt{3}\\x=-\sqrt{3}\end{matrix}\right.\)

c/

\(\left(x^3-x^2\right)^2-4x^2+8x-4=0\)

\(\Leftrightarrow x^4\left(x-1\right)^2-4\left(x-1\right)^2=0\)

\(\Leftrightarrow\left(x-1\right)^2\left(x^4-4\right)=0\)

\(\Leftrightarrow\left(x-1\right)^2\left(x^2-2\right)\left(x^2+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x^2-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\pm\sqrt{2}\end{matrix}\right.\)

Sos

a. x mũ 2 - 2x + 1 = 25 

= x^2 + 2.x.1 + 1^2

= ( x + 1 ) ^2

ko bt có đúng ko nữa, mấy câu kia tui ko bt lm

Sos

\(x^2-y^2+z^2-t^2-2xz+2yt=\)

\(=\left(x^2-2xz+z^2\right)-\left(y^2-2yt+t^2\right)=\)

\(=\left(x-z\right)^2-\left(y-t\right)^2=\)

\(=\left[\left(x-z\right)-\left(y-t\right)\right]\left[\left(x-z\right)+\left(y-t\right)\right]\)

   \(x^2-y^2+z^2-t^2-2xz+2yt\)

\(=\left(x^2-2xz+z^2\right)-\left(y^2+2yt+t^2\right)\)

\(=\left(x-z\right)^2-\left(y-t\right)^2\) 

\(=\left(x-z+y-t\right)\times\left(x-z-y+t\right)\)

\(E=2x^2+5y^2+x+4y+5\)

\(\Rightarrow E=2x^2+x+5y^2+4y+5\)

\(\Rightarrow E=2\left(x^2+\dfrac{1}{2}x+\dfrac{1}{16}-\dfrac{1}{16}\right)+5\left(y^2+\dfrac{4}{5}y+\dfrac{4}{25}-\dfrac{4}{25}\right)+5\)

\(\Rightarrow E=2\left(x^2+\dfrac{1}{2}x+\dfrac{1}{16}\right)+5\left(y^2+\dfrac{4}{5}y+\dfrac{4}{25}\right)+5-\dfrac{1}{8}-\dfrac{4}{5}\)

\(\Rightarrow E=2\left(x+\dfrac{1}{4}\right)^2+5\left(y+\dfrac{2}{5}\right)^2+\dfrac{163}{40}\)

mà \(\left\{{}\begin{matrix}2\left(x+\dfrac{1}{4}\right)^2\ge0,\forall x\\5\left(y+\dfrac{2}{5}\right)^2\ge0,\forall y\end{matrix}\right.\)

\(\Rightarrow E=2\left(x+\dfrac{1}{4}\right)^2+5\left(y+\dfrac{2}{5}\right)^2+\dfrac{163}{40}\ge\dfrac{163}{40}\)

\(\Rightarrow GTNN\left(E\right)=\dfrac{163}{40}\left(tạix=-\dfrac{1}{4};y=-\dfrac{2}{5}\right)\)

1) \(S_{ABCD}=\dfrac{1}{2}.AC.BD\Rightarrow BD=\dfrac{2S_{ABCD}}{AC}=\dfrac{2.50\sqrt[]{3}}{10}=10\sqrt[]{3}\left(cm\right)\)

Gọi O là giao điểm AC và BD

\(\Rightarrow\left\{{}\begin{matrix}OA=\dfrac{1}{2}AC=5\left(cm\right)\\OB=\dfrac{1}{2}BD=5\sqrt[]{3}\left(cm\right)\end{matrix}\right.\)

Xét Δ vuông OAB có :

\(AB^2=OA^2+OC^2=25+25.3=100\left(cm^2\right)\left(Pitago\right)\)

\(\Rightarrow AB=10\left(cm\right)\)

2) Xét Δ vuông OAB có :

\(AB=2OA=10\left(cm\right)\)

⇒ Δ OAB là Δ nửa đều

\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABD}=30^o\\\widehat{BAC}=60^o\end{matrix}\right.\)

mà \(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2\widehat{BAC}\\\widehat{ADC}=\widehat{ABC}=2\widehat{ABD}\end{matrix}\right.\) (tính chất hình thoi)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2.60=120^o\\\widehat{ADC}=\widehat{ABC}=2.30=60^o\end{matrix}\right.\)

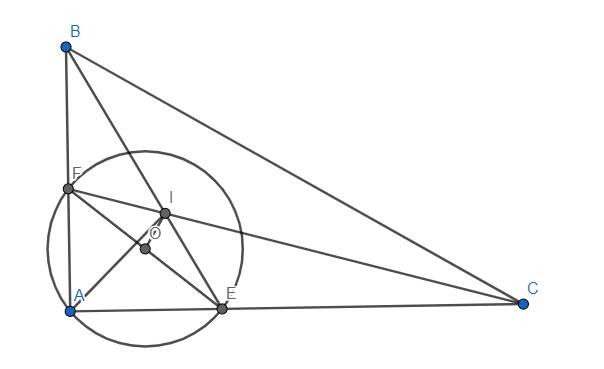
Theo tính chất quen thuộc, O là tâm của (AEF).

Mặt khác, ta lại có \(\widehat{BIC}=90^o+\dfrac{\widehat{BAC}}{2}=135^o\) nên \(\widehat{BIF}=45^o\). Lại có \(\widehat{BAI}=45^o\) nên \(\Delta BIF~\Delta BAI\left(g.g\right)\) \(\Rightarrow\dfrac{BI}{BA}=\dfrac{BF}{BI}\Rightarrow BI^2=BA.BF\) \(\Rightarrow P_{B/\left(O\right)}=P_{B/\left(I;0\right)}\) 

 \(\Rightarrow\) B nằm trên trục đẳng phương của (O) và (I;0). 

 Hoàn toàn tương tự, ta chứng minh được C nằm trên trục đẳng phương của (O) và (I;0). Từ đó suy ra BC là trục đẳng phương của (O) và (I;0) \(\Rightarrow BC\perp OI\) (đpcm)