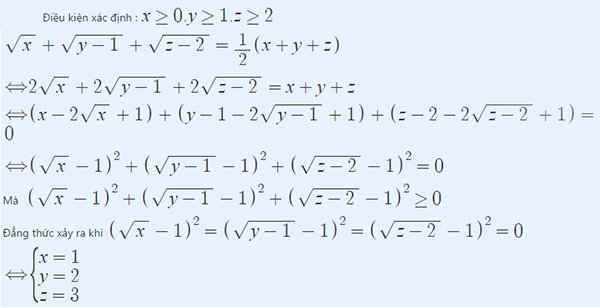ĐKXĐ : \(0\le x\le1\) ; \(\sqrt{x}+\sqrt{1-x}>0\)

Đặt \(\sqrt{x}=a;\sqrt{1-x}=b\left(a;b\ge0\right)\)

=> a² + b² = 1 (1) 

Khi đó phương trình <=> \(\dfrac{2a^3}{a+b}+ab=1\)

<=> 2a³ + ab(a + b) = a + b

<=> 2a³ + a²b + ab² - (a + b) = 0

<=> (a³ + a²b + ab² + b³) - (a + b) + (a³ - b³) = 0

<=> (a + b)(a² + b² - 1) + a³ - b³ = 0 (2) 

Kết hợp (1);(2) được a³ - b³ = 0

<=> a = b

<=> \(\sqrt{x}=\sqrt{1-x}\Leftrightarrow x=\dfrac{1}{2}\)(tm)

Vậy tập nghiệm \(S=\left\{\dfrac{1}{2}\right\}\)

xét A(0;1) ta có: 2.0² + 1 = 1 vậy A  ϵ y = 2x² + 1

xét B(-1,1) ta có : 2.(-1)² + 1 = 3  vậy B \(\notin\)  y = 2x² + 1

xét C(1,3) ta có: 2.1² + 1 = 3 vậy C ϵ y = 2x² + 1

xét D(-2,-4) ta có : 2.(-2)² + 1 = 9 vậy D \(\notin\) y = 2x² + 1

xét E(2,6) ta có : 2.2² + 1 = 9 vậy E \(\notin\) y = 2x² + 1

Bạn thay lần lượt từng điểm vào nhé. Ví dụ A(0,1) ta thay x=0 vào đồ thị ta được kết quả y=1 => A thuộc đồ thị

Tương tự như vậy ta có điểm C(1;3) cũng thuộc đồ thị

\(Đk:x\ge0;y\ge1;z\ge2\)

\(\sqrt{x}+\sqrt{y-1}+\sqrt{z-2}=\dfrac{1}{2}\left(x+y+z\right)\)

\(\Leftrightarrow x+y+z-2\sqrt{x}-2\sqrt{y-1}-2\sqrt{z-2}=0\)

\(\Leftrightarrow\left[x-2\sqrt{x}+1\right]-1+\left[\left(y-1\right)-2\sqrt{y-1}+1\right]+\left[\left(z-2\right)-2\sqrt{z-2}+1\right]+1=0\)

\(\Leftrightarrow\left(\sqrt{x}-1\right)^2+\left(\sqrt{y-1}-1\right)^2+\left(\sqrt{z-2}-1\right)^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{x}-1\right)^2=0\\\left(\sqrt{y-1}-1\right)^2=0\\\left(\sqrt{z-2}-1\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\\z=3\end{matrix}\right.\)

Lần sau lên gg xem có k đi r hãy hỏi nhé :3

\(a,=\sqrt{a}\left(\sqrt{b}-1\right)-\left(\sqrt{b}-1\right)\\ =\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)\\ b,=\sqrt{a}\left(\sqrt{a}+1\right)+2\sqrt{b}\left(\sqrt{a}+1\right)\\ =\left(\sqrt{a}+2\sqrt{b}\right)\left(\sqrt{a}+1\right)\\ c,Sửa:x\sqrt{x}+y\sqrt{y}+x+y\\ =\sqrt{xy}\left(x+y\right)+\left(x+y\right)=\left(\sqrt{xy}+1\right)\left(x+y\right)\\ d,=x+\sqrt{x}-2\sqrt{x}-2\\ =\sqrt{x}\left(\sqrt{x}+1\right)-2\left(\sqrt{x}+1\right)\\ =\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)

\(\sqrt{ab}-\sqrt{a}-\sqrt{b}+1\)

\(=\sqrt{a}\left(\sqrt{b}-1\right)+\left(\sqrt{b}-1\right)\)

\(=\left(\sqrt{a}+1\right)\left(\sqrt{b}-1\right)\)

Mấy ý kia làm tương tự nhá

\(a,x\sqrt{x}+\sqrt{x}-x-1\\ =\sqrt{x}\left(x+1\right)-\left(x+1\right)\\ =\left(\sqrt{x}-1\right)\left(x+1\right)\\ b,\sqrt{ab}+2\sqrt{a}+3\sqrt{b}+6\\ =\sqrt{a}\left(\sqrt{b}+2\right)+3\left(\sqrt{b}+2\right)\\ =\left(\sqrt{a}+3\right)\left(\sqrt{b}+2\right)\)

`a, x sqrt x + sqrt x - x - 1`

`= sqrt x(x+1) - (x+1)`

`= sqrt(x-1)(x+1)`

`b, sqrt a(sqrt b + 2) + 3(sqrt b + 2)`

`= (sqrt a + 3)(sqrt b+2)`

Gọi \(B\left(x_0;y_0\right)\in\left(d\right)\Rightarrow y_0=-x_0+4\)

\(AB=\sqrt{\left(x_0-1\right)^2+\left(y_0-4\right)^2}\\ \Leftrightarrow AB^2=\left(x_0-1\right)^2+\left(-x_0+4-4\right)^2\\ =2x^2_0-2x_0+1=\left(\sqrt{2}x-\dfrac{1}{\sqrt{2}}\right)^2+\dfrac{1}{2}\ge\dfrac{1}{2}\)

Dễ thấy AB nhỏ nhất khi \(\left(\sqrt{2}x_0-\dfrac{1}{\sqrt{2}}\right)^2=0\Rightarrow\sqrt{2}x_0-\dfrac{1}{\sqrt{2}}=0\\ \Rightarrow x_0=\dfrac{1}{\sqrt{2}}:\sqrt{2}=\dfrac{1}{2}\Rightarrow y_0=\dfrac{7}{2}\)

Vậy \(B\left(\dfrac{1}{2};\dfrac{7}{2}\right)\) thì AB bé nhất và bằng \(\dfrac{\sqrt{2}}{2}\)

`\sqrt{x^2}-3x+2`

`=|x|-3x+2`

`@TH1:`\(x \ge 0=>|x|=x\)

  `=>x-3x+2=-2x+2`

`@TH2:x < 0=>|x|=-x`

   `=>-x-3x+2=-4x+2`

x² + \(\dfrac{18x}{5}\) - 64 = 0

△ = (18/5)² -4.(-64) = \(\dfrac{6724}{25}\)

x = { -(18/5) + - (82/5)}: 2

x ϵ {32/5; -10}

`\sqrt{64x+64}-\sqrt{25x+25}+\sqrt{4x+4}=20`     `ĐK: x >= -1`

`<=>8\sqrt{x+1}-5\sqrt{x+1}+2\sqrt{x+1}=20`

`<=>5\sqrt{x+1}=20`

`<=>\sqrt{x+1}=4`

`<=>x+1=16`

`<=>x=15` (t/m)