\(a,5x\left(x^2-9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=9\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ b,3\left(x+3\right)-x^2-3x=0\\ \Leftrightarrow3\left(x+3\right)-x\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(3-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\\ c,x^2-9x-10=0\\ \Leftrightarrow x^2+x-10x-10=0\\ \Leftrightarrow x\left(x+1\right)-10\left(x+1\right)=0\\ \Leftrightarrow\left(x-10\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)

a, 5\(x\)(\(x^2\) - 9) = 0

    \(\left[{}\begin{matrix}x=0\\x^2-9=0\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\) 

Vậy \(x\) \(\in\) { -3; 0; 3}

b, 3.(\(x+3\)) - \(x^2\) - 3\(x\) = 0

    3.(\(x+3\)) - \(x\).( \(x\) + 3) = 0

    (\(x+3\))( 3 - \(x\)) = 0

     \(\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)

Vậy \(x\) \(\in\){ -3; 3}

c, \(x^2\) - 9\(x\) - 10 = 0

   \(x^2\) + \(x\) - 10\(x\)  - 10 = 0

   \(x.\left(x+1\right)\) - 10.( \(x-1\)) = 0

        (\(x+1\))(\(x-10\)) = 0

         \(\left[{}\begin{matrix}x+1=0\\x-10=0\end{matrix}\right.\)

           \(\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)

Vậy \(x\) \(\in\){ -1; 10}

\(a,15x-5xy\\ =5x\left(3-y\right)\\ b,\left(x^2+1\right)^2-4x^2\\ =\left(x^2-x+1\right)\left(x^2+x+1\right)\\ c,x^2-10x-9y^2+25\\ =\left(x-5\right)^2-9y^2\\ =\left(x-9y-5\right)\left(x+9y-5\right)\)

hé lu ông zà

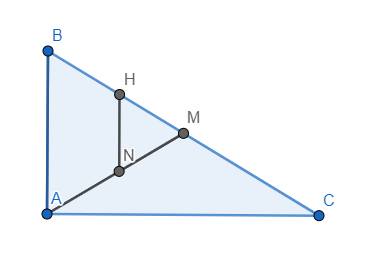
 Ta có \(HN\perp AC\) và \(AB\perp AC\) nên AB//HN. Do đó tứ giác ABHN là hình thang        (1)

 Mặt khác, tam giác ABC vuông tại A có trung tuyến AM nên \(AM=\dfrac{1}{2}BC=BM\), suy ra tam giác MAB cân tại M hay \(\widehat{ABH}=\widehat{NAB}\)           (2)

 Từ (1) và (2), ta suy ra tứ giác ABHN là hình thang cân. (đpcm)

\(\Leftrightarrow4x^2-12x+9+y^2+10y+25=0\)

\(\Leftrightarrow\left(2x-3\right)^2+\left(y+5\right)^2=0\) (1)

Do \(\left(2x-3\right)^2\ge0\) và \(\left(y+5\right)^2\ge0\)

\(\Rightarrow\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3\right)=0\\y+5=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)

\(2x^2-2xy-4x+y^2+4=0\)

\(\Leftrightarrow x^2-2xy+y^2+x^2-4x+4=0\)

\(\Leftrightarrow\left(x-y\right)^2+\left(x-2\right)^2=0\left(1\right)\)

mà \(\left\{{}\begin{matrix}\left(x-y\right)^2\ge0,\forall x;y\\\left(x-2\right)^2\ge0,\forall x\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2=0\\\left(x-2\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

4\(x^2\) + y² - 12\(x\) + 10y + 34 = 0

(4\(x^2\) - 12\(x\) + 9) + (y² + 10y + 25) = 0

(2\(x\) - 3)² + (y + 5)² = 0

(2\(x\) - 3)² ≥ 0 ∀ \(x\); (y + 5)² ≥ 0 ∀ y

(2\(x-3\))² + (y + 5)² = 0 ⇔ \(\left\{{}\begin{matrix}2x-3=0\\y+5=0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)

Kl: (\(x;y\)) = ( \(\dfrac{3}{2}\); -5)

\(4x^2+y^2-12x+10y+34=0\)

\(\Leftrightarrow4x^2-12x+9+y^2+10y+25=0\)

\(\Leftrightarrow\left(2x-3\right)^2+\left(y+5\right)^2=0\left(1\right)\)

mà \(\left\{{}\begin{matrix}\left(2x-3\right)^2\ge0,\forall x\\\left(y+5\right)^2\ge0,\forall y\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3\right)^2=0\\\left(y+5\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x-3=0\\y+5=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)

Ta có : \(4x^2+y^2-12x+10y+34=0\)

\(\Leftrightarrow4x^2-12x+9+y^2+10y+25=0\)

\(\Leftrightarrow\left(2x-3\right)^2+\left(y+5\right)^2=0\left(1\right)\)

Ta thấy : \(\left(2x-3\right)^2;\left(y+5\right)^2\ge0\)

Nên để (1) thoả mãn : 

\(\Leftrightarrow\left\{{}\begin{matrix}2x-3=0\\y+5=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)

Vậy........

\(5^{x+1}-5^x=100\cdot25^{29}\)

\(\Rightarrow5^x\left(5-1\right)=100\cdot\left(5^2\right)^{29}\)

\(\Rightarrow5^x\cdot4=100\cdot5^{58}\)

\(\Rightarrow5^x=\dfrac{100\cdot5^{58}}{4}\)

\(\Rightarrow5^x=25\cdot5^{58}\)

\(\Rightarrow5^x=5^{60}\)

\(\Rightarrow x=60\)

\(5^{x+1}-5x=100.25^{29}\)

\(5.5^x-5^x=4.25.25^{29}\)

\(5^x.\left(5-1\right)4.25^{30}\)

\(4.5^x-4.\left(5^2\right)^{30}\)

\(5x=5^{60}\)

\(x=60\)

tham khảo nhé, phần nào thừa thì bạn có thể ko vt

Góc A = 3. góc D 

góc A + góc D = 1800

Giải bài toán tổng tỉ trên ta được :

góc A = 180:(1+3).3=1350 

góc B - góc C = 30

góc B + góc C = 1800

Giải bài toán tổng hiệu trên ta được : 

Góc B = ( 180+30 ) :2 = 1050

Tổng : góc A + góc B = 1350+1050= 2040

A B E I C D H

Xét hình thang ABCD có

\(\widehat{C}=\widehat{D}=80^o\) => ABCD là hình thang cân => AD=BC

\(\Rightarrow\widehat{A}=180^o-\widehat{D}=180^o-80^o=100^o\) (Hai góc trong cùng phía)

Tương tự ta cũng có \(\widehat{B}=100^o\)

\(\Rightarrow\widehat{A}=\widehat{B}=100^o\)

Xét tg ABC và tg ABD có

AD=BC (cmt)

\(\widehat{A}=\widehat{B}\) (cmt)

AB chung

=> tg ABD = tg ABC (c.g.c) \(\Rightarrow\widehat{ADB}=\widehat{ACB}\)

Mà \(\widehat{ADB}+\widehat{BDC}=\widehat{ADC}=180^o=\widehat{BCD}=\widehat{ACB}+\widehat{ACD}\)

\(\Rightarrow\widehat{BDC}=\widehat{ACD}=\left(180^o-\widehat{CID}\right):2=60^o\)

=> tg CID là tg đều => CD=CI (1)

Xét tg ABI có

\(\widehat{BAC}=\widehat{ACD}=60^o\) (góc so le trong)

\(\widehat{ABD}=\widehat{BDC}=60^o\) (góc so le trong)

\(\widehat{AIB}=\widehat{CID}=60^o\) (góc đối đỉnh)

=> tg ABI là tg đều

Ta có AE là phân giác \(\widehat{BAI}\) (gt)

=> AE là đường trung trực, đường cao của tg ABI (trong tg đều đường phân giác đồng thời là đường cao, đường trung trực)

Xét tg BIE có

AE đồng thời là đường cao và đường trung trực => tg BIE cân tại E

\(\Rightarrow\widehat{DBC}=\widehat{BIE}\) (góc ở đáy tg cân)

Ta có

\(\widehat{DBC}=\widehat{B}-\widehat{ABD}=100^o-60^o=40^o=\widehat{BIE}\)

=> \(\widehat{BEI}=180^o-\left(\widehat{DBC}+\widehat{BIE}\right)=180^o-\left(40^o+40^o\right)=100^o\)

\(\Rightarrow\widehat{IEC}=180^o-\widehat{BEI}=180^o-100^o=80^o\)

Ta có

\(\widehat{BIC}=180^o-\widehat{CID}=180^o-60^o=120^o\)

\(\Rightarrow\widehat{EIC}=\widehat{BIC}-\widehat{BIE}=120^o-40^o=80^o\)

Xét tg CIE có

\(\widehat{IEC}=\widehat{EIC}=80^o\) => tg CIE cân tại C => CE=CI (2)

Từ (1) và (2) => CE=CD