lớp 6a có làm bài thi 15 phút môn toán có kết quả như sau: 5,6,7,8,9,10,10,9,9,8,8,7,5,8,6,9,8,7,7,8,9,6,6,9,8,7,8,9,9,8,10,10,8,8,10,9,8,7,10,9 a)có bao nhiêu bạn làm bài kiểm tra ? b)có bao nhiêu bạn được điểm yếu, trung bình, khá, giỏi ? c)vẽ biểu đồ tranh, dùng mỗi biểu tượng * cho 2 điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b; \(\dfrac{2}{3}\) + \(\dfrac{5}{6}\): 5 - \(\dfrac{1}{18}\).(-3)2
= \(\dfrac{2}{3}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{18}\).9
= \(\dfrac{5}{6}\) - \(\dfrac{1}{2}\)
= \(\dfrac{1}{3}\)
c; \(\dfrac{1}{2}\) + \(\dfrac{-1}{6}\) + \(\dfrac{-1}{12}\) + \(\dfrac{-1}{20}\) + \(\dfrac{-1}{30}\) + \(\dfrac{-1}{42}\)
= \(\dfrac{1}{2}\) - (\(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\))
= \(\dfrac{1}{2}\) - (\(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}-\dfrac{1}{7}\))
= \(\dfrac{1}{2}\) - (\(\dfrac{1}{2}\) - \(\dfrac{1}{7}\))
= \(\dfrac{1}{2}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{7}\)
= \(\dfrac{1}{7}\)

Vì A là trung điểm của OM nên
OM = 2OA = 7 x 2 = 14 (cm)
Vì B là trung điểm của ON nên
ON = 2OB = 11 x 2 = 22 (cm)
MN = ON - OM = 22 - 14 = 8 (cm)
Bạn tham khảo:
Để tính độ dài MN, ta sử dụng định lí về trung điểm:
Nếu A là trung điểm của OM và B là trung điểm của ON, thì AB sẽ là đường chính giữa của hình chữ nhật O AMN. Vì AB là đường chính giữa, nên AB sẽ cắt MN tại trung điểm C.
Do đó, ta có MN = 2 X MC
Ta cần tính độ dài MC. Vì M là trung điểm của OA, nên MC = 1/2 OA
Từ đây, ta có:
MC = 1/2 OA = 1/2 7cm = 3.5cm
Do đó:
MN = 2 x MC = 2 x 3.5 = 7cm
Vậy, độ dài MN là 7cm
#hoctot

\(M=1+2.\left(\dfrac{3}{2.5}+\dfrac{5}{5.10}+\dfrac{7}{10.17}+\dfrac{9}{17.26}\right)\)
\(=1+2\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{17}+\dfrac{1}{17}-\dfrac{1}{26}\right)\)
\(=1+2\left(\dfrac{1}{2}-\dfrac{1}{26}\right)\)
\(=1+1-\dfrac{1}{13}=\dfrac{25}{13}\)

Đặt \(A=\dfrac{1}{2^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}\)
\(=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\right)\)
Đặt \(B=1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{50^2}< \dfrac{1}{49\cdot50}=\dfrac{1}{49}-\dfrac{1}{50}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
=>\(B=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}< 2-\dfrac{1}{50}\)
=>\(A=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\right)< \dfrac{1}{2^2}\left(2-\dfrac{1}{50}\right)=\dfrac{1}{2}-\dfrac{1}{200}< \dfrac{1}{2}\)
\(\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{4}\right)^2+\left(\dfrac{1}{6}\right)^2+...+\left(\dfrac{1}{100}\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}.\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}.\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{2}.\dfrac{1}{50}\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2.\left[1+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{50}\right)^2\right]\)
Ta có:
\(\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2.2}< \dfrac{1}{2.1}=\dfrac{2-1}{2.1}=\dfrac{2}{2.1}-\dfrac{1}{2.1}=1-\dfrac{1}{2}\)
\(\left(\dfrac{1}{3}\right)^2=\dfrac{1}{3.3}< \dfrac{1}{3.2}=\dfrac{3-2}{3.2}=\dfrac{3}{3.2}-\dfrac{2}{3.2}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\left(\dfrac{1}{50}\right)^2=\dfrac{1}{50.50}< \dfrac{1}{50.49}=\dfrac{50-49}{50.49}=\dfrac{50}{50.49}-\dfrac{49}{50.49}=\dfrac{1}{49}-\dfrac{1}{50}\)
Khi đó
\(1+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{50}\right)^2< 1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}=2-\dfrac{1}{50}< 2\)
\(=\left(\dfrac{1}{2}\right)^2.\left[1+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{50}\right)^2\right]< \dfrac{1}{4}.2=\dfrac{1}{2}\)
Vậy \(\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{4}\right)^2+\left(\dfrac{1}{6}\right)^2+...+\left(\dfrac{1}{100}\right)^2< \dfrac{1}{2}\left(đpcm\right)\)
Tick cho mk nha :>>



A = \(\dfrac{n+4}{3n+5}\) (n \(\ne\) - \(\dfrac{5}{3}\))
A \(\in\) Z ⇔ n + 4 \(⋮\) 3n + 5
3(n + 4) ⋮ 3n + 5
3n + 12 ⋮ 3n + 5
3n + 5 + 7 ⋮ 3n + 5
7 ⋮ 3n + 5
3n + 5 \(\in\) Ư(7) = {-7; -1; 1; 7}
Lập bảng ta có:
| 3n + 5 | - 7 | - 1 | 1 | 7 |
| n | - 4 | - 2 | - \(\dfrac{4}{3}\) | \(\dfrac{2}{3}\) |
| A = \(\dfrac{n+4}{3n+5}\) | 0 | - 2 | \(\dfrac{8}{3}\) | \(\dfrac{2}{3}\) |
| A \(\in\) Z | loại | loại |
Theo bảng trên ta có n \(\in\) {-4; - 2}
Kết luận A = \(\dfrac{n+4}{3n+5}\) có giá trị nguyên khi và chi khi n \(\in\) {- 4; - 2}
Ta có:
Để \(\dfrac{n+4}{3n+5}\) đạt giá trị nguyên thì \(\left(n+4\right)⋮\left(3n+5\right)\)
\(\Rightarrow3\left(n+4\right)⋮3n+5\)
\(\Rightarrow\left(3n+5+7\right)⋮\left(3n+5\right)\)
\(\Rightarrow7⋮\left(3n+5\right)\)
\(\Rightarrow3n+5\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow3n\in\left\{-12;-6;-4;2\right\}\)
\(\Rightarrow n\in\left\{-4;-2;-\dfrac{4}{3};\dfrac{2}{3}\right\}\)

\(-\dfrac{3}{7}-\dfrac{1}{4}.\dfrac{3}{7}+\dfrac{3}{7}.\dfrac{5}{4}\\ =\dfrac{3}{7}.\left(-1-\dfrac{1}{4}+\dfrac{5}{4}\right)\\ =\dfrac{3}{7}.0\\ =0\)
\(\dfrac{-3}{7}-\dfrac{1}{4}.\dfrac{3}{7}+\dfrac{3}{7}.\dfrac{5}{4}\)
=\(\dfrac{-3}{7}-\dfrac{3}{28}+\dfrac{15}{28}\)
=\(\dfrac{-15}{28}+\dfrac{15}{28}\)
=\(0\)
\(#LilyVo\)
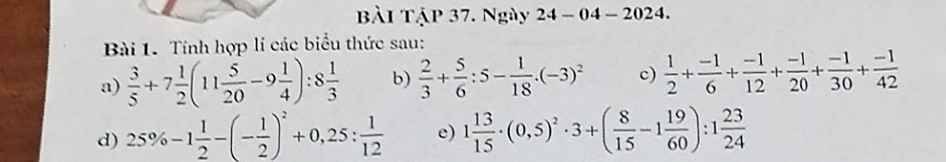
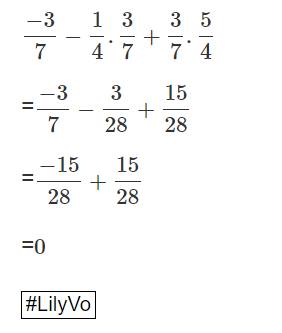
1101000011000100
12345678901234567