Ta có \(A=\overset{2n}{11...1}+\overset{n}{44...4}+1\)

\(A=\dfrac{1}{9}.\overset{2n}{99...9}+\dfrac{4}{9}.\overset{n}{99...9}+1\)

\(A=\dfrac{1}{9}\left(10^{2n}-1\right)+\dfrac{4}{9}\left(10^n-1\right)+1\)

\(A=\dfrac{10^{2n}-1+4.10^n-4+9}{9}\)

\(A=\dfrac{\left(10^n\right)^2+4.10^n+4}{9}\)

\(A=\left(\dfrac{10^n+2}{3}\right)^2\) 

 Dễ thấy \(10^n+2⋮3\) vì có tổng các chữ số là 3 nên \(\dfrac{10^n+2}{3}\inℕ^∗\). Vậy A là số chính phương (đpcm)

Lời giải:

\(ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-2}{2}=1\)

Khi đó:

\(\text{VT}=\frac{a}{ab+bc+ac+a^2}+\frac{2b}{ab+bc+ac+b^2}+\frac{3c}{ab+bc+ac+c^2}\)

\(=\frac{a}{(a+b)(a+c)}+\frac{2b}{(b+a)(b+c)}+\frac{3c}{(c+a)(c+b)}\)

\(=\frac{a(b+c)+2b(a+c)+3c(a+b)}{(a+b)(b+c)(c+a)}\)

\(=\frac{3ab+4ac+5bc}{(a+b)(b+c)(c+a)}=\text{VP}\)

Lời giải:

$x^2-y^2+a^2-b^2+2ax+2by=(x^2+a^2+2ax)-(y^2+b^2-2by)$

$=(x+a)^2-(y-b)^2=(x+a-y+b)(x+a+y-b)$

\(E=-4x^2+x+1\)

\(\Rightarrow E=-4\left(x^2-\dfrac{x}{4}\right)+1\)

\(\Rightarrow E=-4\left(x^2-\dfrac{x}{4}+\dfrac{1}{64}\right)+1+\dfrac{1}{16}\)

\(\Rightarrow E=-4\left(x-\dfrac{1}{8}\right)^2+\dfrac{17}{16}\)

 mà \(-4\left(x-\dfrac{1}{8}\right)^2\le0,\forall x\)

\(\Rightarrow E=-4\left(x-\dfrac{1}{8}\right)^2+\dfrac{17}{16}\le\dfrac{17}{16}\)

\(\Rightarrow GTLN\left(E\right)=\dfrac{17}{16}\left(tạix=\dfrac{1}{8}\right)\)

\(F=5x-3x^2+6\)

\(\Rightarrow F=-3\left(x^2-\dfrac{5x}{3}\right)+6\)

\(\Rightarrow F=-3\left(x^2-\dfrac{5x}{3}+\dfrac{25}{36}\right)+6+\dfrac{25}{12}\)

\(\Rightarrow F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{12}\)

mà \(-3\left(x-\dfrac{5}{6}\right)^2\le0,\forall x\)

\(\Rightarrow F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{12}\le\dfrac{97}{12}\)

\(\Rightarrow GTLN\left(F\right)=\dfrac{97}{12}\left(tạix=\dfrac{5}{6}\right)\)

\(x\) mũ bao nhiêu thì cô và các bạn mới giúp được chứ em?

7) Chứng minh rằng: x^2 +4y^2 + z^2- 2x -6z +8y + 15 > 0 với mọi x, y, z.

Ta có hình vẽ:

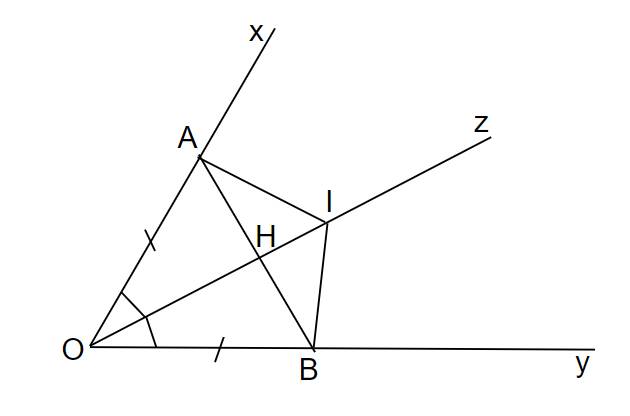
a) Vì Oz là phân giác của xOy nên xOz=yOz=xOy2���=���=���2

Xét Δ AOI và Δ BOI có:

OA = OB (gt)

AOI = BOI (cmt)

OI là cạnh chung

Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)

b) Xét Δ AOH và Δ BOH có:

OA = OB (gt)

AOH = BOH (câu a)

OH là cạnh chung

Do đó, Δ AOH = Δ BOH (c.g.c)

=> AHO = BHO (2 góc tương ứng)

Mà AHO + BHO = 180^o (kề bù) nên AHO = BHO = 90^o

=> AB⊥OI(đpcm))

A B C H M I

a/ Xét tg vuông BAC và tg vuông HAB có

\(\widehat{ACB}=\widehat{ABH}\) (cùng phụ với \(\widehat{BAC}\) )

b/

\(BC=\sqrt{AC^2-AB^2}\) (Pitago)

\(\Rightarrow BC=\sqrt{25^2-15^2}=20cm\)

\(\dfrac{MA}{AB}=\dfrac{MC}{BC}\) (T/c đường phân giác)

\(\Rightarrow\dfrac{MA}{15}=\dfrac{MC}{25}\Rightarrow\dfrac{MA}{MC}=\dfrac{15}{25}=\dfrac{3}{5}\)

\(\Rightarrow MC=\dfrac{AC}{3+5}x5=\dfrac{25}{8}x5=15,625cm\)

c/

\(AB^2=AH.AC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)

\(\Rightarrow AH=\dfrac{AB^2}{AC}\)

AM=AC-MC

HM=AM-AH

\(BH^2=AH.HC\)(trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)

Xét tg vuông BHM

\(BM=\sqrt{BH^2+HM^2}\)

Ta có

\(AB\perp BC;MI\perp BC\) => MI//AB

\(\Rightarrow\dfrac{BI}{AM}=\dfrac{CI}{MC}\Rightarrow\dfrac{BI}{CI}=\dfrac{AM}{MC}\) (talet trong tg)

Từ đó tính được CI

Bạn tự thay số và tính toán

\(a.\) Xét \(\Delta BAC\) và \(\Delta HAB\) \(\left(\widehat{B}=\widehat{H}=90^o\right)\), ta có:
\(\widehat{A}\) là góc chung
\(\Rightarrow\Delta BAC\sim\Delta HAB\) \(\left(g-g\right)\)
\(b.\) Xét \(\Delta ABC\) vuông tại \(\widehat{B}\), ta có:
\(AC^2=AB^2+BC^2\) \(\left(Pytago\right)\)
\(\Rightarrow BC^2=AC^2-AB^2=25^2-15^2=625-225=400\)
\(\Rightarrow BC=\sqrt{400}=20\) \(\left(cm\right)\)
Do \(BM\) là đường phân giác của \(\Delta ABC\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{BC}{MC}\) \(\Rightarrow\dfrac{AB}{AC-MC}=\dfrac{BC}{MC}\)
\(\Rightarrow AB\cdot MC=BC\cdot\left(AC-MC\right)\)
\(\Leftrightarrow AB\cdot MC=AC\cdot BC-BC\cdot MC\)
\(\Leftrightarrow AB\cdot MC+BC\cdot MC=AC\cdot BC\)
\(\Leftrightarrow MC\left(AB+BC\right)=AC\cdot BC\)
\(\Leftrightarrow MC=\dfrac{AC\cdot BC}{AB+BC}=\dfrac{25\cdot20}{15+20}=\dfrac{500}{35}=\dfrac{100}{7}\approx14,29\) \(\left(cm\right)\)

\(E=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)\)
Đặt \(t=x^2+5x+5\) ta được
\(E=\left(x-1\right)\left(x+1\right)\)
\(=x^2-1\)
\(x^2\ge0\) \(\Rightarrow x^2-1\ge-1\)
Dấu "\(=\)" xảy ra khi \(x=0\)
Vậy giá trị nhỏ nhất của \(E\) là \(-1\)

Em đặt t thì p là t chứ sao lại đặt t xuống dưới là x được.