a) Do BM là đường trung tuyến của ∆ABC (gt)

⇒ M là trung điểm của AC

Do D và B đối xứng qua M (gt)

⇒ M là trung điểm của BD

Tứ giác ABCD có:

M là trung điểm của AC (cmt)

M là trung điểm của BD (cmt)

⇒ ABCD là hình bình hành

b) Do ABCD là hình bình hành (cmt)

⇒ AB // CD

Mà DH ⊥ AB

⇒ DH ⊥ AC

c) Do ABCD là hình bình hành

⇒ AB // CD

Mà BK ⊥ CD

⇒ BK ⊥ AB

⇒ ∠KBH = 90⁰

Tứ giác BHDK có:

∠BKD = ∠KBH = ∠BHD = 90⁰

⇒ BHDK là hình chữ nhật

Mà M là trung điểm BD

⇒ M là trung điểm của HK

⇒ M, H, K thẳng hàng

Do đó chứng minh MH ⊥ MK là sai. Em xem lại đề ở câu c nhé

Đề bài của em đâu? Phải có đề bài thì cô và các bạn mới giúp em được 

a) \(x\left(y-7\right)+y-12=0\left(x;y\inℤ\right)\)

\(\Rightarrow x\left(y-7\right)+y-7-5=0\)

\(\Rightarrow\left(x+1\right)\left(y-7\right)=5\)

\(\Rightarrow\left(x+1\right);\left(y-7\right)\in U\left(5\right)=\left\{-1;1;-5;5\right\}\)

\(\Rightarrow\left(x;y\right)\in\left\{\left(-2;2\right);\left(0;12\right);\left(-6;6\right);\left(4;8\right)\right\}\)

b) xy - 6x - 4y + 13 = 0

x(y - 6) - 4y + 24 - 11 = 0

x(y - 6) - 4(y - 6) = 11

(y - 6)(x - 4) = 11

TH1: x - 4 = 1 và y - 6 = 11

*) x - 4 = 1

x = 5

*) y - 6 = 11

y = 17

TH2: x - 4 = -1 và y - 6 = -11

*) x - 4 = -1

x = 3

*) y - 6 = -11

y = -5

TH3: x - 4 = 11 và y - 6 = 1

*) x - 4 = 11

x = 15

*) y - 6 = 1

y = 7

TH4: x - 4 = -11 và y - 6 = -1

*) x - 4 = -11

x = -7

*) y - 6 = -1

y = 5

Vậy ta có các cặp giá trị (x; y) sau:

(-7; 5); (15; 7); (3; -5); (5; 17)

Ta có: \(\widehat{HAF}+\widehat{FAB}+\widehat{DAB}+\widehat{DAH}=360^o\)

Mà \(\widehat{FAB}=\widehat{DAH}=90^O\)

\(\Rightarrow\widehat{HAF}+\widehat{DAB}=180^o\)

Ta lại có: \(\widehat{ADC}+\widehat{DAB}=180^o\) ( 2 góc trong cùng phía nên kề bù với nhau )

\(\Rightarrow\widehat{HAF}=\widehat{ADC}\)

Xét \(\Delta HAF\) và \(\Delta ADC\) có:

\(HA=HD\left(gt\right)\)

\(\widehat{HAF}=\widehat{ADC}\left(CMT\right)\)

\(AF=DC\left(gt\right)\)

Vậy \(\Delta HAF\) \(=\) \(\Delta ADC\) \(\left(c.g.c\right)\)

\(\Rightarrow AC=FH\) ( 2 cạnh tưng ứng )

b) Ta có: \(\widehat{CBE}=\widehat{ABC}+90^o\)

\(\widehat{GDC}=\widehat{ADC}+90^o\)

Mà \(\widehat{ADC}=\widehat{ABC}\)

\(\Rightarrow\widehat{CBE}=\widehat{GDC}\)

Xét \(\Delta CBE\) và \(\Delta GDC\) ta có:

\(EB=CD\left(gt\right)\)

\(\widehat{CBE}=\widehat{GDC}\left(CMT\right)\)

\(CB=GD\left(gt\right)\)

Vậy \(\Delta CBE=\Delta GDC\left(c.g.c\right)\)

\(\Rightarrow CE=GC\) ( 2 cạnh tương ứng )

\(\Rightarrow\Delta CEG\) cân tại \(G\)

a) Ta biết rằng trong hình bình hành ABCD, các đường chéo chia nhau đều và cắt nhau ở trung điểm.

Vì vậy, ta có AC = FH.

b) Vì ABFE là hình vuông, nên các cạnh AB và FE là song song và bằng nhau.

Tương tự, vì ADGH là hình vuông, nên các cạnh AD và GH cũng là song song và bằng nhau. Do đó, ta có AB || FE và AD || GH. Vì AC = FH (chứng minh ở câu a), và AB || FE, AD || GH,

nên theo tính chất của các đường song song, ta có AC || FH. Do đó, AC vuông góc với FH.

c) Ta biết rằng trong hình vuông, các đường chéo chia nhau đều và cắt nhau vuông góc.

Vì vậy, ta có AG ⊥ CE và CG ⊥ AE. Vì AG ⊥ CE, nên AGC là tam giác vuông tại G.

Vì CG ⊥ AE, nên CEG là tam giác vuông tại C. Vì AG = GC (vì AGC là tam giác vuông cân), nên ta cũng có CG = GC.

Do đó, ta có CEG là tam giác vuông cân.

Vậy, ta đã chứng minh được a), b), c) trong đề bài.

\(\left(a^6-b^3\right)=\left(a^2-b\right)\left(a^4+a^2b+b^2\right)\)

\(=\left(a^2-b\right)\left(a^4+a^2b+b^2\right)\)

\(a.x^2-7x-3x+21=0\Leftrightarrow\left(x^2-7x\right)-\left(3x-21\right)=0\)

\(\Leftrightarrow x\left(x-7\right)-3\left(x-7\right)=0\Leftrightarrow\left(x-3\right)\left(x-7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=7\end{matrix}\right.\)

\(b.x^2+6x+2x+12=0\Leftrightarrow\left(x^2+6x\right)+\left(2x+12\right)=0\)

\(\Leftrightarrow x\left(x+6\right)+2\left(x+6\right)=0\Leftrightarrow\left(x+2\right)\left(x+6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-6\end{matrix}\right.\)

\(c.x^2+4x+5x+20=0\Leftrightarrow\left(x^2+4x\right)+\left(5x+20\right)=0\)

\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\Leftrightarrow\left(x+5\right)\left(x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-4\end{matrix}\right.\)

\(Ax=Bx\Rightarrow Ax-Bx=0\Rightarrow x\left(A-B\right)=0\Rightarrow x=0\) \(\rightarrow câu.A\)

A.(0)
B.(1)
C(0,1,5)
D.(0,1,5,6)
chọn đáp án thôi là đc ak

Lời giải:

a. $x^2-y^2+8x-8y=(x^2-y^2)+(8x-8y)$

$=(x-y)(x+y)+8(x-y)=(x-y)(x+y+8)$

b. $4x^2+4xy+y^2-4x-2y=(4x^2+4xy+y^2)-(4x+2y)$

$=(2x+y)^2-2(2x+y)=(2x+y)(2x+y-2)$

c.

$x^3+y^3+4x+4y=(x^3+y^3)+(4x+4y)$

$=(x+y)(x^2-xy+y^2)+4(x+y)$

$=(x+y)(x^2-xy+y^2+4)$

d.

$=(x^3-3x^2y+3xy^2-y^3)+(x^2-y^2)=(x-y)^3+(x-y)(x+y)$

$=(x-y)[(x-y)^2+(x+y)]=(x-y)(x^2-2xy+y^2+x+y)$

e.

$x^2+3x+2=(x^2+x)+(2x+2)=x(x+1)+2(x+1)$

$=(x+1)(x+2)$

f.

$x^2-7x+6=(x^2-6x)-(x-6)=x(x-6)-(x-6)=(x-1)(x-6)$

h.

Đa thức không phân tích được thành nhân tử với hệ số nguyên.

bằng 2

2 nhé

​

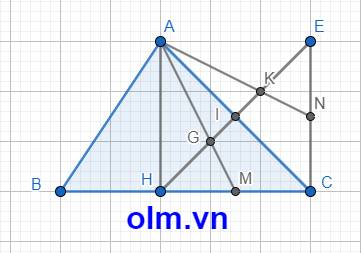
a, Xét tứ AHCE ta có: IH = IE ; IA = IC 

⇒ tứ giácAHCE là hình bình hành (1)

Mà AH \(\perp\)  BC \(\equiv\)  H nên ⇒ \(\widehat{AHC}\) = 90⁰ (2)

Kết hợp (1) và (2) ta có: Tứ giác AHCE là hình chữ nhật (đpcm).

b, Xét tam giác AHC có: M là trung  điểm HC; I là trung điểm AC

⇒ AM; HI lần lượt là trung tuyến của tam  giác AHC

⇒ G là trọng tâm của tam giác AHC ⇒ HG = \(\dfrac{2}{3}\)HI ⁽³⁾

IG = HI - HG = HI - \(\dfrac{2}{3}\)HI = \(\dfrac{1}{3}\)HI 

Chứng minh tương tự ta có: KE = \(\dfrac{2}{3}\)IE = \(\dfrac{2}{3}\)HI ⁽⁴⁾ ( vì IE = HI)

IK = IE - KE =  IE - \(\dfrac{2}{3}\)IE = \(\dfrac{1}{3}\)IE = \(\dfrac{1}{3}\)HI (vì HI = IE)

GK = IG + IK = \(\dfrac{1}{3}\)HI + \(\dfrac{1}{3}\)HI = \(\dfrac{2}{3}\)HI ⁽⁵⁾  

Kết hợp(3); (4); (5) ta có: HG = GK = KE (đpcm)