a) Gọi hai phần được chia đó lần lượt là x và y 

Hai phần này tỉ lệ thuận với 2 và 3 nên ta có:

\(\dfrac{x}{2}=\dfrac{y}{3}\) và \(x+y=120\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có: 

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{120}{5}=24\)

\(\Rightarrow\dfrac{x}{2}=24\Rightarrow x=48\)

\(\Rightarrow\dfrac{y}{3}=24\Rightarrow y=72\)

Vậy: .... 

b) Gọi hai phần được chia đó lần lượt là a và b

Hai phần này tỉ lệ nghịch với 3 và 4 nên ta có:

\(3a=4b\)

\(\Rightarrow\dfrac{3a}{12}=\dfrac{4b}{12}\)

\(\Rightarrow\dfrac{a}{4}=\dfrac{b}{3}\)

Mà: \(a+b=112\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{a}{4}=\dfrac{b}{3}=\dfrac{a+b}{4+3}=\dfrac{112}{7}=16\)

\(\Rightarrow\dfrac{a}{4}=16\Rightarrow a=64\)

\(\Rightarrow\dfrac{b}{3}=16\Rightarrow b=48\)

Vậy: ... 

a:Vì O là tâm đường tròn ngoại tiếp ΔABC

mà O là trung điểm của AK

nên AK là đường kính của (O)

Xét (O) có

ΔABK nội tiếp

AK là đường kính

Do đó: ΔABK vuông tại B

=>\(\widehat{ABK}=90^0\)

Xét (O) có

ΔACK nội tiếp

AK là đường kính

Do đó; ΔACK vuông tại C

=>\(\widehat{ACK}=90^0\)

b: H là trực tâm của ΔABC

=>BH\(\perp\)AC và CH\(\perp\)AB

Ta có: BH\(\perp\)AC

CK\(\perp\)CA

Do đó: BH//CK

ta có: CH\(\perp\)AB

BK\(\perp\)AB

Do đó: CH//BK

Xét tứ giác BHCK có

BH//CK

BK//CH

Do đó: BHCK là hình bình hành

=>BC cắt HK tại trung điểm của mỗi đường

=>M là trung điểm của HK

Xét ΔAHK có

M,O lần lượt là trung điểm của KH,KA

=>MO là đường trung bình của ΔAHK

=>MO=1/2HA

=>AH=2MO

Gọi hai số cần tìm là a,b

Tổng của hai số là 32 nên a+b=32

Hai số tỉ lệ với 7/2 và 9/2 nên \(\dfrac{a}{\dfrac{7}{2}}=\dfrac{b}{\dfrac{9}{2}}\)

=>\(\dfrac{a}{3,5}=\dfrac{b}{4,5}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{3,5}=\dfrac{b}{4,5}=\dfrac{a+b}{3,5+4,5}=\dfrac{32}{8}=4\)

=>\(a=4\cdot3,5=14;b=4\cdot4,5=18\)

Vậy: Hai số cần tìm là 14 và 18

a: Xét ΔMAB và ΔMCD có

MA=MC

\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)

MB=MD

Do đó; ΔMAB=ΔMCD

=>AB=CD

mà AB=AC

nên CD=CA

=>ΔCDA cân tại C

b: Ta có: CD=CA

mà CA=CE

nên CD=CA=CE

=>\(CD=\dfrac{1}{2}AE\)

Xét ΔDAE có

DC là đường trung tuyến

\(DC=\dfrac{1}{2}AE\)

Do đó: ΔDAE vuông tại D

a) Vì : \(\left(2x-y+z\right)^{2024}\ge0,\left|y^2-z\right|\ge0,\left(z-4\right)^{2022}\ge0\forall x,y,z\\ \Rightarrow\left(2x-y+z\right)^{2024}+\left|y^2-z\right|+\left(z-4\right)^{2022}\ge0\)

Dấu "=" xảy ra khi : 2x-y+z=y^2-z=z-4=0

Với z-4=0=>z=4

Lại có : y^2-z=0=>y^2=4=>y=2 hoặc y=-2

+) y=2=>2x-2+4=0=>x=-1

+) y=-2=>2x-(-2)+2=0=>x=-2

Vậy (x;y;z)=(-1;2;4);(-2;-2;4)

b) x+y-2xy=4

=> 2x+2y-4xy=8

=> 2x(1-2y)+2y=8

=> 2x(1-2y)-(1-2y)=7

=> (1-2y)(2x-1)=7

Do x, y đều là các số nguyên => 1-2y và 2x-1 cũng là các số nguyên

Mà : 7=1.7=(-1).(-7)

Đến đây bạn lập bảng giá trị rồi kết luận nhé.

a) \(A\left(-1\right)=-1+\left(-1\right)^2+\left(-1\right)^3+...+\left(-1\right)^{99}+\left(-1\right)^{100}\\ =-1+1+\left(-1\right)+...+\left(-1\right)+1\\ =0\)

=> x=-1 là nghiệm đa thức A(x)

b) \(A\left(\dfrac{1}{2}\right)=\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3+...+\left(\dfrac{1}{2}\right)^{99}+\left(\dfrac{1}{2}\right)^{100}\\ \Rightarrow2.A\left(\dfrac{1}{2}\right)=1+\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{98}+\left(\dfrac{1}{2}\right)^{99}\\ \Rightarrow2.A\left(\dfrac{1}{2}\right)-A\left(\dfrac{1}{2}\right)=1-\left(\dfrac{1}{2}\right)^{100}\\ \Rightarrow A\left(\dfrac{1}{2}\right)=\dfrac{2^{100}-1}{2^{100}}\)

Có thể phân biệt bằng cách:

- nếu như đại lượng này tăng và đại lượng kia cũng tăng thì là tỉ lệ thuận

- nếu như đại lượng này tăng và đại lượng kia giảm thì là đại lượng tỉ lệ nghịch

 \(\Rightarrow\) vì \(|\)\(x|\) o mà về phải luôn > = 3 về trái cũng phải luôn \(\ge\) 3\(x\ge\) o

\(\Rightarrow\) 2024 \(\times1011x-< =1012x+3\)

\(x=5\)

vậy \(x=\) 5 sẽ thỏa mãn yêu cầu bài toán

có ai làm câu d chưa cho mình xin hướng dẫn ạ

Câu 4:

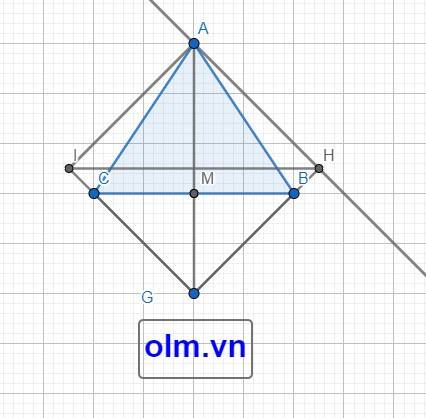
Vì tam giác ABC cân tại A; AM là đường cao của tam giác ABC

Nên AM là trung trực của BC (trong tam giác cân đường cao cũng là đường trung trực của tam giác)

⇒ GC = GB ⇒ tam giác BCG cân tại G

  ⇒ GM là phân giác của góc CGB (vì trong tam giác cân đường cao cũng là đường phân giác)

⇒ \(\widehat{CGM}\) = \(\dfrac{1}{2}\) \(\widehat{BGC}\) = 90⁰ x \(\dfrac{1}{2}\) = 45⁰

Xét tam giác vuông AIG có: 

\(\widehat{IAG}\) = 90⁰ - \(\widehat{IGA}\) = 90⁰ - 45⁰ = 45⁰

⇒ \(\widehat{IGA}\) = \(\widehat{IAG}\) = 45⁰

⇒ tam giác AIG vuông cân tại I

⇒ IA = IG

AH // GI ⇒ AH \(\perp\) AI (vì một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại)

 \(\widehat{IAH}\) = 90⁰

Xét tứ giác: AHGI có:

\(\widehat{IAH}\) = \(\widehat{AIG}\) = \(\widehat{IGH}\) = 90⁰; IA = IG (cmt)

⇒ AHGI là hình vuông

⇒ AG \(\perp\) HI  (tính chất hai đường chéo của hình vuông)

Mặt khác  AG \(\perp\) BC (gt)

⇒ HI // BC (vì hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)

Kết Luận: HI // BC (đpcm)

Khi x=-3 thì \(\left(x^{2023}+3x^{2022}+1\right)^{2000}=\left[\left(-3\right)^{2023}+3\cdot\left(-3\right)^{2022}+1\right]^{2000}\)

\(=\left[-3^{2023}+3^{2023}+1\right]^{2000}\)

\(=1^{2000}=1\)