Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 2<3
=>\(2+8,5\cdot6< 3+8,5\cdot6\)
b: 2<3
=>\(\sqrt{2}< \sqrt{3}\)
=>\(-\sqrt{2}>-\sqrt{3}\)
=>\(30-\sqrt{2}>30-\sqrt{3}\)
c:
Vì 3>2
nên \(3\sqrt{3}>3\sqrt{2}\)
=>\(-3\sqrt{3}< -3\sqrt{2}\)
mà 35<36
nên \(35-3\sqrt{3}< 36-3\sqrt{2}\)

13: \(x^3-6x^2+12x-8\)
\(=x^3-3\cdot x^2\cdot2+3\cdot x\cdot2^2-2^3\)
\(=\left(x-2\right)^3\)
14: \(8x^3+12x^2y+6xy^2+y^3\)
\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2+y^3\)
\(=\left(2x+y\right)^3\)
16: \(x^{10}-1=\left(x^5-1\right)\left(x^5+1\right)=\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)\left(x+1\right)\left(x^4-x^3+x^2-x+1\right)\)
17: \(x^2-9=x^2-3^2=\left(x-3\right)\left(x+3\right)\)
18: \(4x^2-25=\left(2x\right)^2-5^2=\left(2x-5\right)\left(2x+5\right)\)
19: \(x^4-y^4=\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
20: \(9x^2+6xy+y^2=\left(3x\right)^2+2\cdot3x\cdot y+y^2=\left(3x+y\right)^2\)
21: \(6x-9-x^2=-\left(x^2-6x+9\right)\)
\(=-\left(x^2-2\cdot x\cdot3+3^2\right)\)
\(=-\left(x-3\right)^2\)
22: \(x^2+4xy+4y^2=x^2+2\cdot x\cdot2y+\left(2y\right)^2=\left(x+2y\right)^2\)
23: \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)\left(x+y+x-y\right)\)
\(=2x\cdot2y=4xy\)
24: \(\left(x+y+z\right)^2-4z^2\)
\(=\left(x+y+z\right)^2-\left(2z\right)^2\)
\(=\left(x+y+z-2z\right)\left(x+y+z+2z\right)\)
\(=\left(x+y-z\right)\left(x+y+3z\right)\)
25: \(\left(3x+1\right)^2-\left(x+1\right)^2\)
\(=\left(3x+1-x-1\right)\left(3x+1+x+1\right)\)
\(=2x\left(4x+2\right)=4x\left(2x+1\right)\)
26: \(x^3y^3+125=\left(xy\right)^3+5^3\)
\(=\left(xy+5\right)\left(x^2y^2-5xy+25\right)\)
27: \(8x^3-y^3-6xy\left(2x-y\right)\)
\(=\left(2x-y\right)\left(4x^2+2xy+y^2\right)-6xy\left(2x-y\right)\)
\(=\left(2x-y\right)\left(4x^2+2xy+y^2-6xy\right)\)
\(=\left(2x-y\right)\left(4x^2-4xy+y^2\right)=\left(2x-y\right)^3\)
28: \(\left(3x+2\right)^2-2\left(x-1\right)\left(3x+2\right)+\left(x-1\right)^2\)
\(=\left(3x+2-x+1\right)^2\)
\(=\left(2x+3\right)^2\)

Bài 4:
a: 4x-y=1
=>y=4x-1
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=4x-1\end{matrix}\right.\)
b: x+3y=-2
=>x=-3y-2
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=-3y-2\end{matrix}\right.\)
Bài 5:
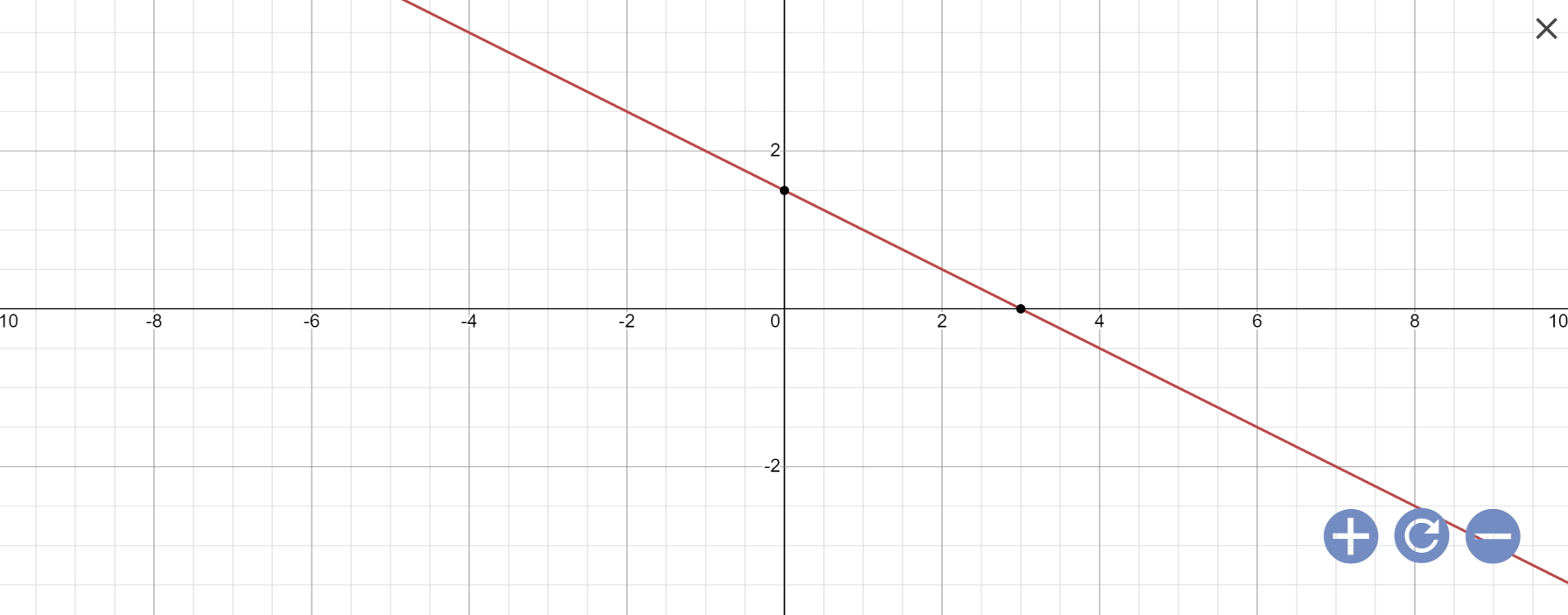
x+2y-3=0
=>2y=-x+3
=>\(y=\dfrac{-x+3}{2}\)
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{-x+3}{2}\end{matrix}\right.\)
Biểu diễn tập nghiệm:

Bài 1:
\(3^{39}< 3^{40}=\left(3^4\right)^{10}=81^{10}\)
\(11^{21}>11^{20}=121^{10}\)
mà 121>81
nên \(11^{21}>3^{39}\)
Bài 2:
\(5^{27}=\left(5^3\right)^9=125^9;2^{63}=\left(2^7\right)^9=128^9\)
mà 125<128
nên \(5^{27}< 2^{63}\)
\(2^{63}=\left(2^9\right)^7=512^7;5^{28}=\left(5^4\right)^7=625^7\)
mà 512<625
nên \(2^{63}< 5^{28}\)
Do đó: \(5^{27}< 2^{63}< 5^{28}\)

a: Xét ΔABC có D,E lần lượt là trung điểm của AC,AB
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\dfrac{BC}{2}=2\left(cm\right)\)
Xét hình thang BEDC có
M,N lần lượt là trung điểm của EB,DC
=>MN là đường trung bình của hình thang BEDC
=>MN//ED//BC và \(MN=\dfrac{ED+BC}{2}=\dfrac{2+4}{2}=3\left(cm\right)\)
b: Xét ΔBED có MP//ED
nên \(\dfrac{MP}{ED}=\dfrac{BM}{BE}=\dfrac{1}{2}\)
=>\(MP=\dfrac{1}{2}ED=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{4}BC\)
Xét ΔCED có NQ//ED
nên \(\dfrac{NQ}{ED}=\dfrac{CN}{CD}=\dfrac{1}{2}\)
=>\(NQ=\dfrac{1}{2}ED=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{4}BC\)
\(MN=\dfrac{1}{2}\left(ED+BC\right)=\dfrac{1}{2}\left(\dfrac{1}{2}BC+BC\right)=\dfrac{1}{2}\cdot\dfrac{3}{2}BC=\dfrac{3}{4}BC\)
=>\(MP+PQ+QN=\dfrac{3}{4}BC\)
=>\(PQ=\dfrac{3}{4}BC-\dfrac{1}{4}BC-\dfrac{1}{4}BC=\dfrac{1}{4}BC\)
Do đó:MP=PQ=QN

Vậy số thứ hai sẽ bằng 10/100số thứ nhất , số thứ ba sẽ bằng 1/100 số thứ nhất
Số thứ 3 là :
256,077:(100+10+1)=2,307
Rồi bạn tìm số thứ nhất, thứ hai nhé
Gọi số thập phân cần tìm là \(x\)
Dịch dấu phẩy sang phải tức là tăng \(10\) lần,sang trái tức à giảm \(10\) lần
Theo bài ra ,ta có:
\(x+x\times10+x:10=256,077\)
\(x+x\times10+x\times0,1=256,077\)
\(x\times\left(1+10+0,1\right)=256,077\)
\(x\times11,1=256,077\)
\(x=256,077:11,1\)
\(x=23,07\)
Vậy số cần tìm là \(23,07\)

\(a.4x-6y=2\left(2x-3y\right)\\ b.x^2+6x+9-y^2\\ =\left(x+3\right)^2-y^2\\ =\left(x-y+3\right)\left(x+y+3\right)\\ c.4x^2-9y^2\\ =\left(2x\right)^2-\left(3y\right)^2\\ =\left(2x-3y\right)\left(2x+3y\right)\\ d.x^2-x-y^2+y\\ =\left(x^2-y^2\right)-\left(x-y\right)\\ =\left(x+y\right)\left(x-y\right)-\left(x-y\right)\\ =\left(x-y\right)\left(x+y-1\right)\\ e.x^2-4y^2-6x+9\\ =\left(x^2-6x+9\right)-4y^2\\ =\left(x-3\right)^2-\left(2y\right)^2\\ =\left(x-2y-3\right)\left(x+2y-3\right)\\ f.x^4-y^4+4y^2-4\\ =x^4-\left(y^4-4y^2+4\right)\\ =\left(x^2\right)^2-\left(y^2-2\right)^2\\ =\left(x^2-y^2+2\right)\left(x^2+y^2-2\right)\)

Câu 2:
\(A=x^2-10x+1\\ =\left(x^2-10x+25\right)-24\\ =\left(x-5\right)^2-24\ge-24\forall x\)
Dấu "=" xảy ra: `x-5=0<=>x=5`
\(B=x^2-5x+2\\ =\left(x^2-5x+\dfrac{25}{4}\right)-\dfrac{17}{4}\\ =\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2\right)-\dfrac{17}{4}\\ =\left(x-\dfrac{5}{2}\right)^2-\dfrac{17}{4}\ge-\dfrac{17}{4}\forall x\)
Dấu "=" xảy ra: `x-5/2=0<=>x=5/2`
Câu 2
A = x² - 10x + 1
= x² + 2.x.5 + 25 - 24
= (x + 5)² - 24
Do (x + 5)² ≥ 0 với mọi x ∈ R
⇒ (x + 5)² - 24 ≥ -24 (với mọi x ∈ R)
Vậy GTNN của A là -24 khi x = -5
B = x² - 5x + 2
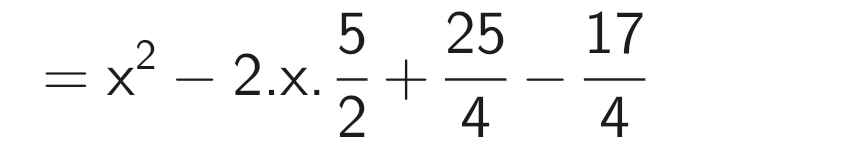
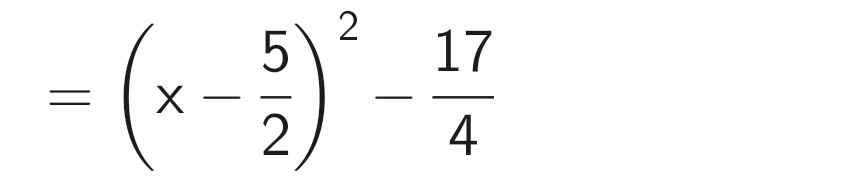
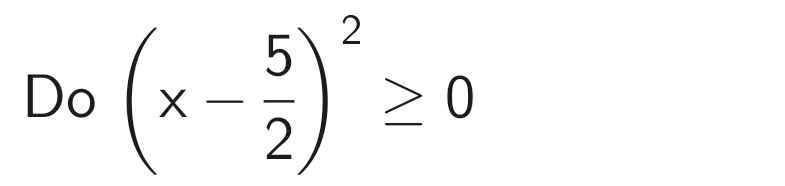
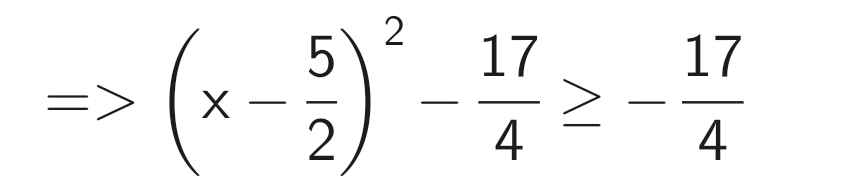
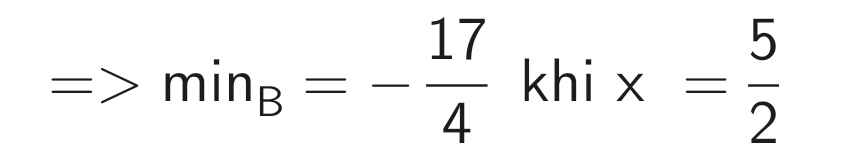
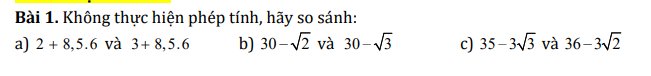

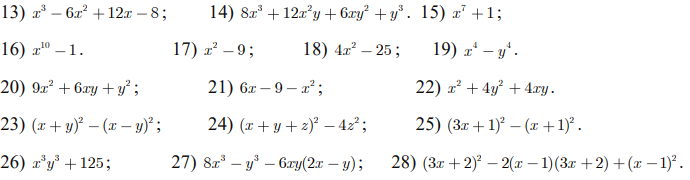


a: 2a+3>2b+3
=>2a>2b
=>a>b
b: -3a-1>=-3b-1
=>\(-3a>=-3b\)
=>3a<=3b
=>a<=b
c: 5-2a<5-a-b
=>5-2a+a<5-b
=>5-a<5-b
=>a-5>b-5
=>a>b