cho tam giác ABC có góc ACB<gócABC<90 độ. kề AD vuông góc với BC
(D thuộc BC ) . lấy m là trung điểm của AD . trên tia đối của MB lấy E sao cho ME=MB trên tia đối MC lấy F sao cho MF=MC. chứng minh rằng :
a.AE=BD
b.so sánh BD và CD
c.ba điểm AEF thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bổ sung đề; MB\(\perp\)OB tại B
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)(OM là phân giác của góc AOB)
Do đó: ΔOAM=ΔOBM
=>MA=MB
b: Ta có: ΔOAM=ΔOBM
=>OA=OB
=>ΔOAB cân tại O
c: Xét ΔMAD vuông tại A và ΔMBE vuông tại B có
MA=MB
\(\widehat{AMD}=\widehat{BME}\)(hai góc đối đỉnh)
Do đó: ΔMAD=ΔMBE
=>MD=ME

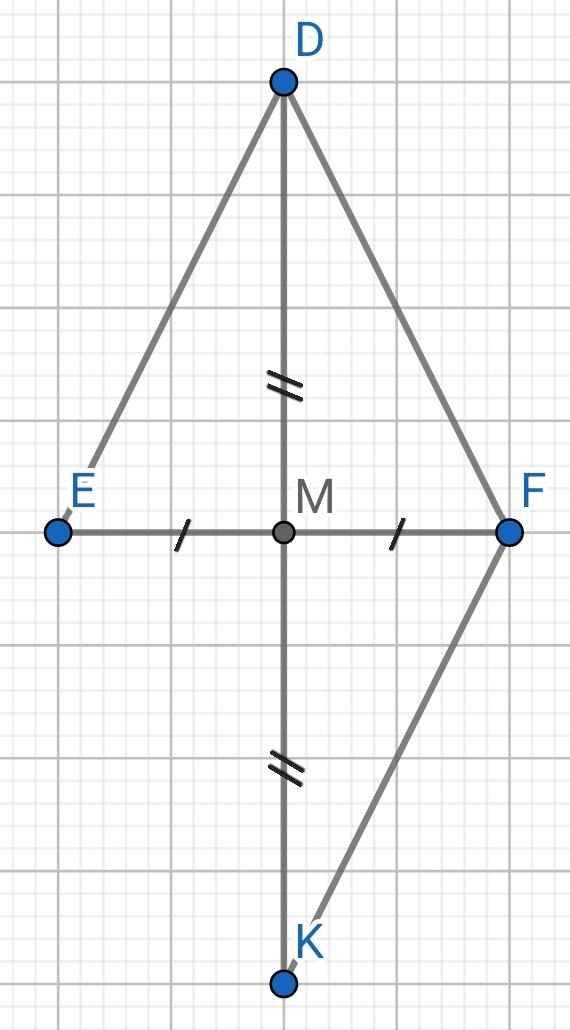
a) Do ∆DEF cân tại D (gt)
⇒ DE = DF
Do M là trung điểm của EF (gt)
⇒ ME = MF
Xét ∆DEM và ∆DFM có:
DE = DF (cmt)
DM là cạnh chung)
ME = MF (cmt)
⇒ ∆DEM = ∆DFM (c-c-c)
b) Sửa đề: Chứng minh DM ⊥ EF
Do ∆DEM = ∆DFM (cmt)
⇒ ∠DME = ∠DMF (hai góc tương ứng)
Mà ∠DME + ∠DMF = 180⁰ (kề bù)
⇒ ∠DME = ∠DMF = 180⁰ : 2 = 90⁰
⇒ DM ⊥ EF
c) Xét ∆DEM và ∆KFM có:
DM = KM (gt)
∠DME = ∠KMF (đối đỉnh)
ME = MF (cmt)
⇒ ∆DEM = ∆KFM (c-g-c)
⇒ DE = KF (hai cạnh tương ứng)
Mà DE = DF (cmt)
⇒ KF = DF
⇒ ∆FDK cân tại F
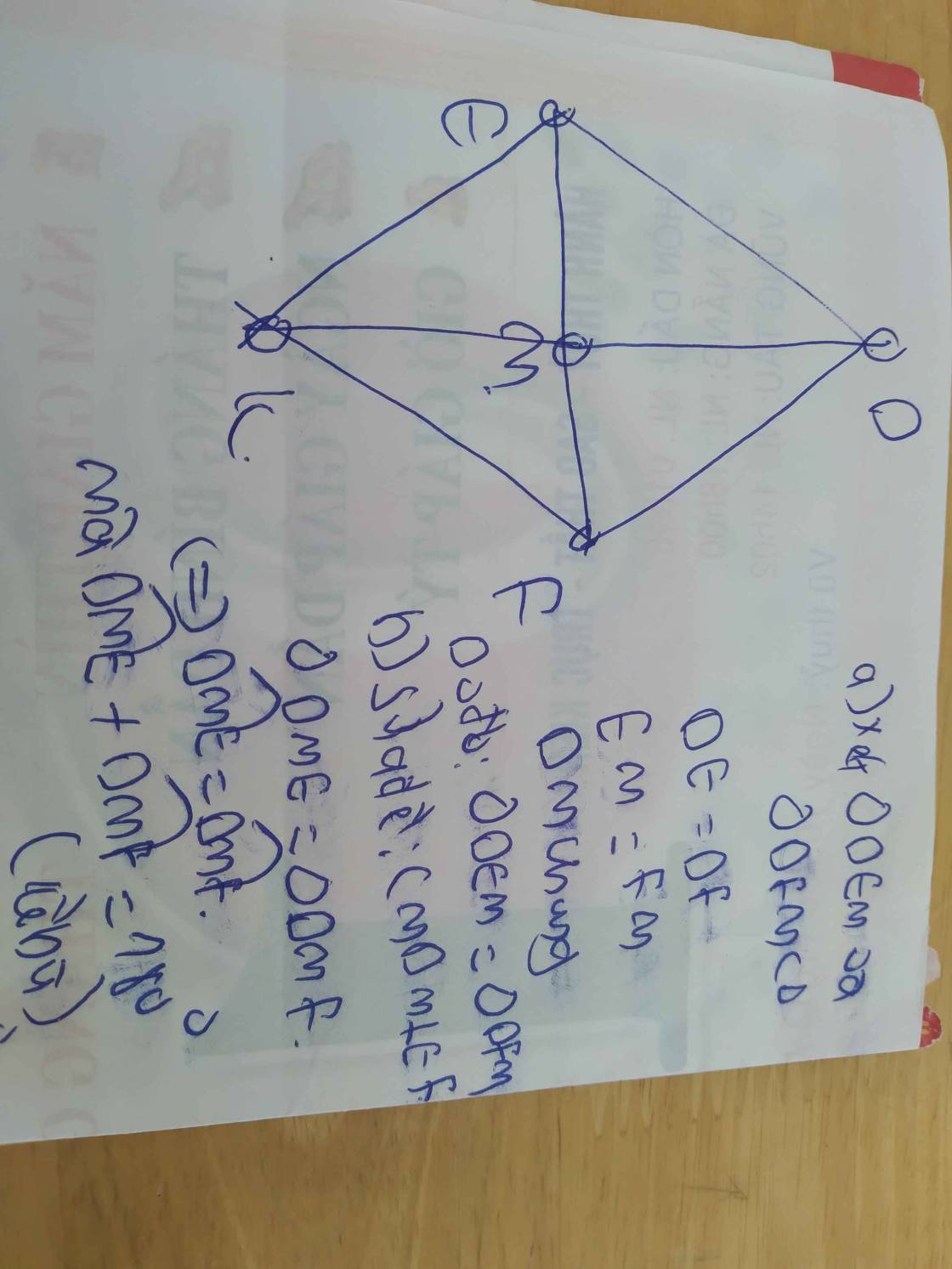
a) tìm ba số x,y,z biết x/3=y/4=z/5 và x.y.z=480
b) tìm ba số a,b,c biết a/4=b/8=c/16 và a^2-b^2=-60

a) Ta có :
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\)
\(\Rightarrow k^3=\dfrac{x}{3}.\dfrac{y}{4}.\dfrac{z}{5}=\dfrac{480}{3.4.5}=8\)
\(\Rightarrow k=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=2\\\dfrac{y}{4}=2\\\dfrac{z}{5}=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=8\\z=10\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=6\\y=8\\z=10\end{matrix}\right.\)
b) Ta có :
\(\dfrac{a}{4}=\dfrac{b}{8}=\dfrac{c}{16}\)
\(\Rightarrow\left(\dfrac{a}{4}\right)^2=\left(\dfrac{b}{8}\right)^2=\left(\dfrac{c}{16}\right)^2\)
\(\Rightarrow\dfrac{a^2}{16}=\dfrac{b^2}{64}=\dfrac{c^2}{256}\)
Áp dụng TCDTSBN, ta có :
\(\dfrac{a^2}{16}=\dfrac{b^2}{64}=\dfrac{c^2}{256}=\dfrac{a^2-b^2}{16-64}=\dfrac{-60}{-48}=\dfrac{5}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a^2}{16}=\dfrac{5}{4}\\\dfrac{b^2}{64}=\dfrac{5}{4}\\\dfrac{c^2}{256}=\dfrac{5}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2=4.5\\b^2=16.5\\c^2=256.5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\pm2\sqrt[]{5}\\b=\pm4\sqrt[]{5}\\c=\pm16\sqrt[]{5}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=\pm2\sqrt[]{5}\\b=\pm4\sqrt[]{5}\\c=\pm16\sqrt[]{5}\end{matrix}\right.\)

a) Áp dụng TCDTSBN, ta có :
\(\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{4}=\dfrac{2x-4y+z}{1.2-4.2+4}=\dfrac{-6}{-2}=3\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{1}=3\\\dfrac{y}{2}=3\\\dfrac{z}{4}=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=6\\z=12\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=3\\y=6\\z=12\end{matrix}\right.\)
b) Áp dụng TCDTSBN, ta có :
\(\dfrac{a}{2}=\dfrac{b}{-4}=\dfrac{c}{6}=\dfrac{a-5b+4c}{2-5.\left(-4\right)+4.6}=\dfrac{23}{46}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{2}=\dfrac{1}{2}\\\dfrac{b}{-4}=\dfrac{1}{2}\\\dfrac{c}{4}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=2\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=1\\b=-2\\c=2\end{matrix}\right.\)

A B C H K I M
a/
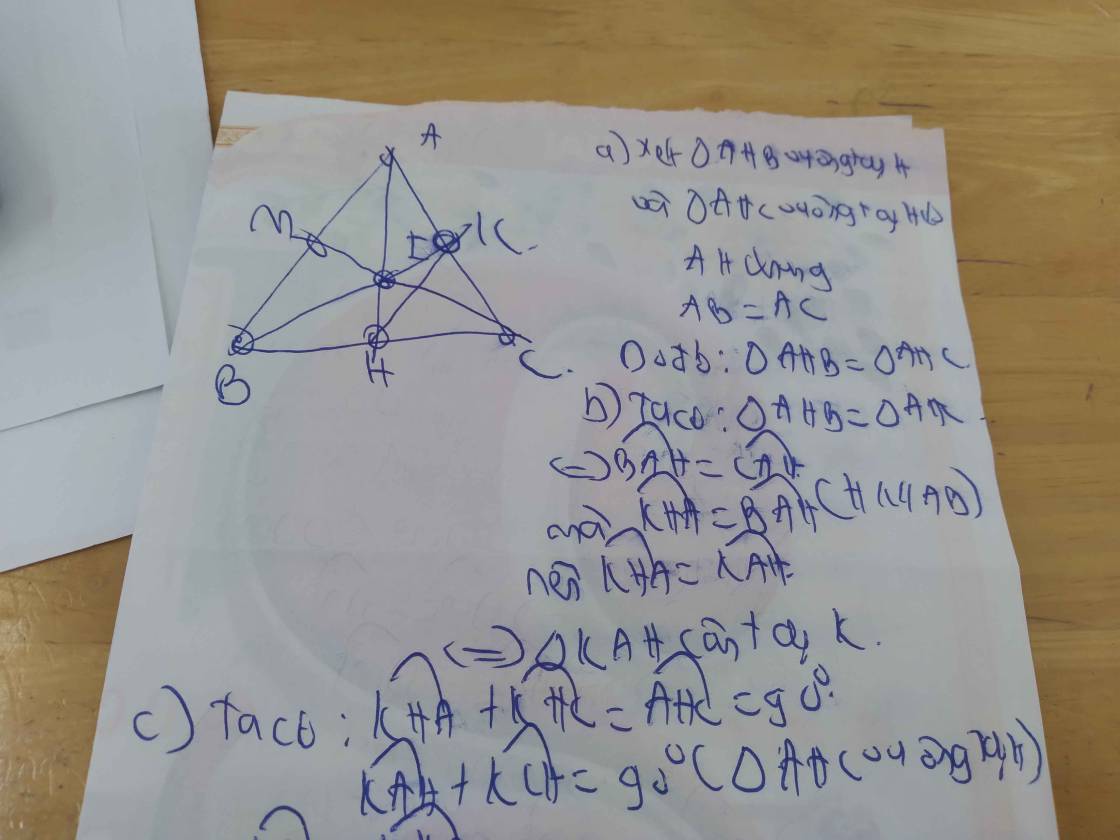
Xét tg vuông AHB và tg vuông AHC có
AB = AC (cạnh bên tg cân)
HB = HC (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)
=> tg AHB = tg AHC (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
b/
Xét tg ABC có
HB = HC (cmt); HK//AB (gt) => KA=KC (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
Xét tg vuông AHC có
KA=KC (cmt)
\(\Rightarrow HK=KA=KC=\dfrac{AC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg AHK cân tại K
c/
Xét tg vuông ABC có
HB=HC (cmt); KA=KC (cmt) => I là trọng tâm của tg ABC
=> CI là trung uyến của tg ABC (trong tg 3 đường trung tuyến đồng quy) \(\Rightarrow M\in CI\) => C, I, M thẳng hàng

A B C M A'
Kéo dài AM cắt BC tại A'.
Xét ΔABA' ta có BĐT: AB + BA' > AA' = MA + MA'
hay AB + BA' > MA + MA' (1)
Xét ΔCMA' ta có BĐT: CA' > MC - MA' (2) Cộng theo vế (1) và (2) ta được:
(AB + BA' ) + CA' > ( MA + MA' ) + ( MC - MA' ) <===> AB + (BA' + CA') > MA + MC
Hay: AB + CB > MA + MC (I) Chứng minh tương tự ta có:
AB + AC > MB + MC (II)
CB + AC > MA + MB (III) Cộng theo vế (I),(II) và (III) ta được:
2(AB+AC+CB) > 2(MA + MB + MC)
Hay: MA+MB+MC < AB+AC+CB (đpcm).

Số nguyên dương này không thể xác định vì số chữ số của số đó chưa xác định là bao nhiêu.

B=2.2/1.3 . 3.3/2.4 . 4.4/3.5 ......20.20/19.21
=2.3.4.....20/1.2.3.....19 . 2.3.4....20/3.4.5.....21
=20 . 2/21
=40/21

a: Quãng đường xe đạp đi được trong 2 giờ đầu tiên là:
2*20=40(km)
Quãng đường xe đạp đi được từ giớ thứ 3 đến lúc gặp ô tô là:
20(x-2)(km)
Độ dài quãng đường xe đạp đi được cho đến lúc gặp ô tô là:
20(x-2)+40=20x(km)
b: Độ dài quãng đường ô tô đi được cho đến lúc gặp xe đạp là:
60(x-2)(km)
c: Theo đề, ta có:
20x=60(x-2)
=>60x-120=20x
=>40x=120
=>x=3

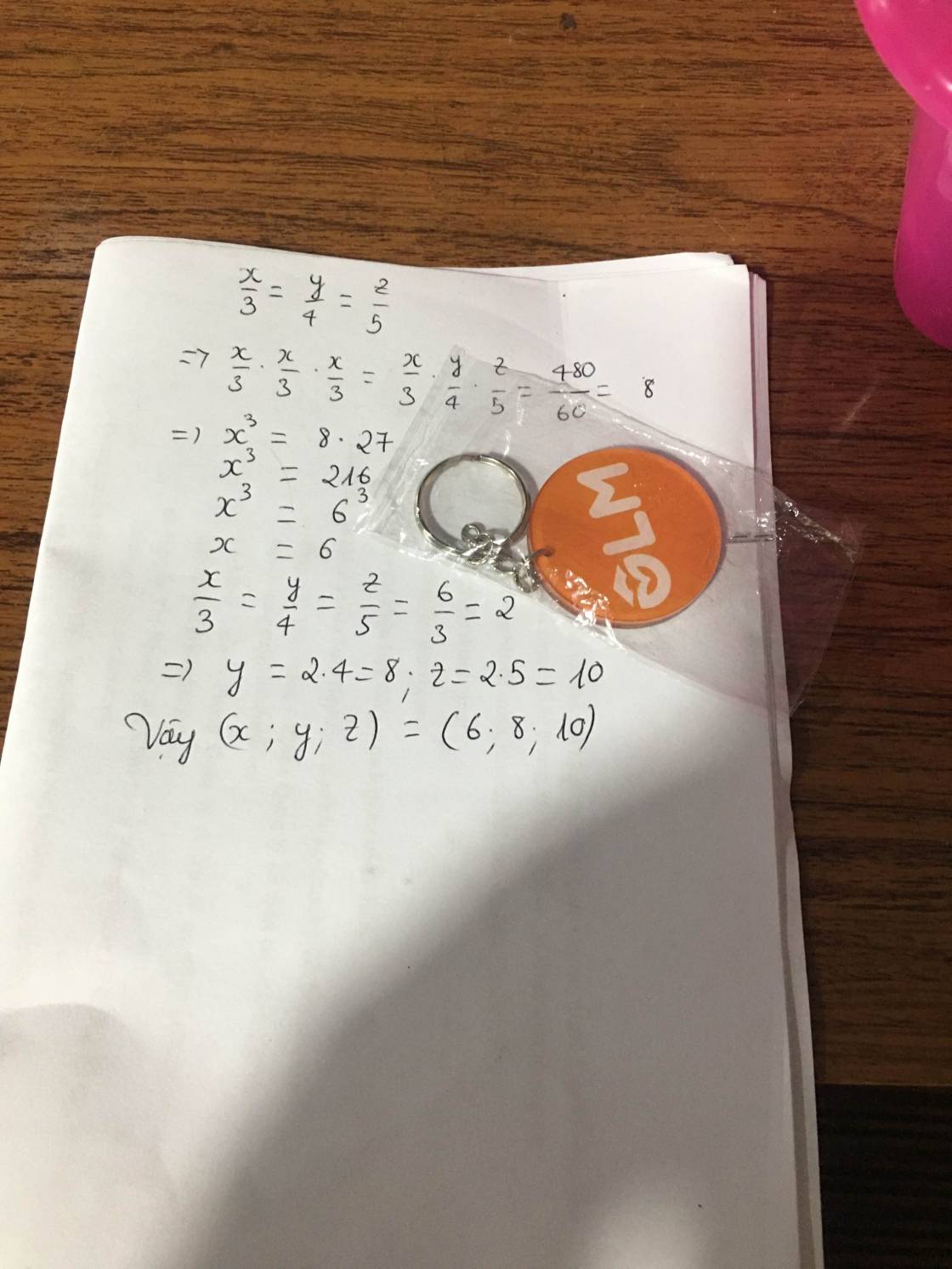


a: Xét ΔMAE và ΔMDB có
MA=MD
\(\widehat{AME}=\widehat{DMB}\)(hai góc đối đỉnh)
ME=MB
Do đó: ΔMAE=ΔMDB
=>AE=BD
b: Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}\)
mà AB,AC lần lượt là cạnh đối diện của các góc ACB,ABC
nên AB<AC
Xét ΔABC có AB<AC
mà BD,CD lần lượt là hình chiếu của AB,AC trên BC
nên BD<CD
c: Xét ΔMAF và ΔMDC có
MA=MD
\(\widehat{AMF}=\widehat{DMC}\)(hai góc đối đỉnh)
MF=MC
Do đó: ΔMAF=ΔMDC
=>\(\widehat{MAF}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//DC
=>AF//BC
Ta có: ΔMAE=ΔMDB
=>\(\widehat{MAE}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BD
=>AE//BC
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng