a: \(M\left(x\right)=N\left(x\right)+E\left(x\right)\)

=>N(x)=M(x)-E(x)

\(=3x^2+4x+1-x^3+3x^2+3x+1=-x^3+6x^2+7x+2\)

b: \(M\left(1\right)=3\cdot1^2+4\cdot1+1=8\)>0

=>x=1 không là nghiệm của M(x)

Ta có: \(x:2=y:3\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{y-x}{3-2}=\dfrac{1}{1}=1\)

Do đó:

\(\dfrac{x}{2}=1=>x=2.1=2\)

\(\dfrac{y}{3}=1=>y=3.1=3\)

Vậy x = 2; y = 3.

`#NqHahh`

Sửa bài:

Ta có: \(x:2=y:3=>\dfrac{x}{2}=\dfrac{y}{3}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{2}=\dfrac{y}{3}=>\dfrac{y-x}{3-2}=\dfrac{-1}{1}=-1\)

Do đó:

\(\dfrac{x}{2}=-1=>x=2.\left(-1\right)=-2\)

\(\dfrac{y}{3}=-1=>y=3.\left(-1\right)=-3\)

Vậy x = -2; y = -3.

`#NqHahh`

5: M nằm trên đường trung trực của EF

=>ME=MF

N nằm trên đường trung trực của EF

=>NE=NF

Xét ΔMEN và ΔMFN có

ME=MF

NE=NF

MN chung

Do đó; ΔMEN=ΔMFN

Bài 4:

AB=AC

=>A nằm trên đường trung trực của BC(1)

Ta có: DB=DC

=>D nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra AD là đường trung trực của BC

=>AD\(\perp\)BC tại trung điểm của BC

=>M là trung điểm của BC

Bài 5

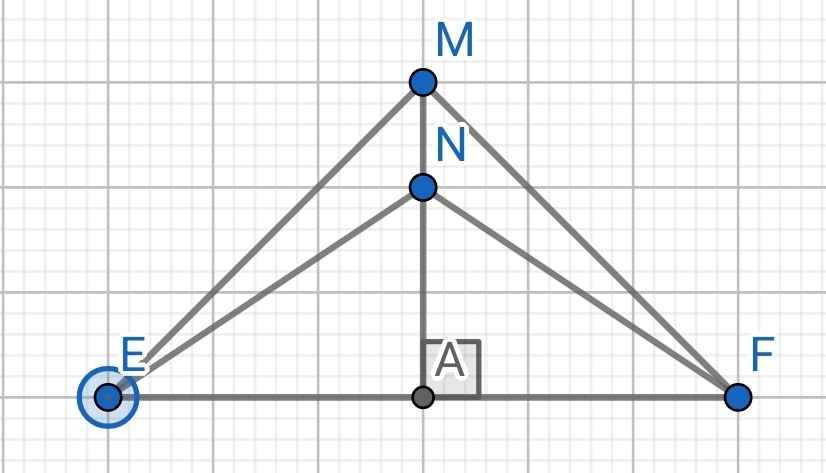
Do M nằm trên đường trung trực của EF (gt)

⇒ ME = MF

Do N nằm trên đường trung trực của EF (gt)

⇒ NE = NF

Xét ∆EMN và ∆FMN có:

MN là cạnh chung

ME = MF (cmt)

NE = NF (cmt)

⇒ ∆EMN = ∆FMN (c-c-c)

a là đường trung trực của AB

=>a\(\perp\)AB

mà B\(\in\)AC

nên a\(\perp\)AC

b là đường trung trực của BC

=>b\(\perp\)BC

mà B\(\in\)AC

nên b\(\perp\)AC

Ta có: a\(\perp\)AC

b\(\perp\)AC

Do đó: a//b

Ta có: a và b lần lượt là đường trung trực của các đoạn thẳng AB và BC nên \(a \bot AB,b \bot BC\).

Mà ba điểm A, B, C thẳng hàng với nhau nên đường thẳng a và b không cắt nhau và chúng cùng vuông góc với đường thẳng chứa ba điểm A, B, C.

Vậy a // b. 

Phương trình bậc 2 có dạng  a+b+c=0

\(\Rightarrow x_1=1;x_2=\dfrac{c}{a}=\dfrac{13}{5}\)

Ta có:

a + b + c = 5 + (-18) + 13 = 0

Phương trình có hai nghiệm:

x₁ = 1; x₂ = 13/5

Ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM\(\perp\)BC và AM là phân giác của \(\widehat{BAC}\)

Gọi O là trung điểm của AD

=>O là tâm đường tròn đường kính AD

Vì \(\widehat{AHD}=\widehat{AMD}=\widehat{AKD}=90^0\)

nên A,H,D,M,K cùng thuộc đường tròn đường kính AD

=>A,H,D,M,K cùng thuộc (O)

Xét (O) có

\(\widehat{MHK}\) là góc nội tiếp chắn cung MK

\(\widehat{MAK}\) là góc nội tiếp chắn cung MK

Do đó: \(\widehat{MHK}=\widehat{MAK}\)(2)

Xét (O) có

\(\widehat{MKH}\) là góc nội tiếp chắn cung MH

\(\widehat{MAH}\) là góc nội tiếp chắn cung MH

Do đó: \(\widehat{MKH}=\widehat{MAH}\left(2\right)\)

Ta có: AM là phân giác của góc BAC

=>\(\widehat{BAM}=\widehat{CAM}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\widehat{MHK}=\widehat{MKH}\)

=>ΔMHK cân tại M

=>MH=MK

Đặt f(x)=0

=>2x-2+6=0

=>2x+4=0

=>2x=-4

=>x=-2

a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}+52^0=90^0\)

=>\(\widehat{ABC}=38^0\)

b: Xét ΔMAB vuông tại A và ΔMCD vuông tại C có

MA=MC

\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)

Do đó: ΔMAB=ΔMCD

c: Ta có: ΔMAB=ΔMCD

=>MB=MD

Xét ΔMAD và ΔMCB có

MA=MC

\(\widehat{AMD}=\widehat{CMB}\)(hai góc đối đỉnh)

MD=MB

Do đó: ΔMAD=ΔMCB

=>\(\widehat{MAD}=\widehat{MCB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AD//BC

d: ta có: ΔMAB=ΔMCD

=>AB=CD

mà \(BI=IA=\dfrac{BA}{2};CK=KD=\dfrac{CD}{2}\)

nên BI=IA=CK=KD

Xét ΔMAI vuông tại A và ΔMCK vuông tại C có

MA=MC

AI=CK

Do đó; ΔMAI=ΔMCK

=>\(\widehat{AMI}=\widehat{CMK}\)

mà \(\widehat{AMI}+\widehat{IMC}=180^0\)(hai góc kề bù)

nên \(\widehat{IMC}+\widehat{KMC}=180^0\)

=>I,M,K thẳng hàng