a/

Xét tứ giác BMCD có

NB=NC (gt)

ND=NM (gt)

=> BMCD là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

b/

Để BMCD là hình thoi \(\Rightarrow MD\perp BC\) (Hình thoi có 2 đường chéo vuông góc) (1)

Ta có

MA=MC (gt)

NB=NC (gt)

=> MN là đường trung bình của tg ABC => MN//AB => MD//AB (2)

Từ (1) và (2) \(\Rightarrow AB\perp BC\)

Để BMCD là hình thoi => tg ABC là tg vuông tại B

a) Tứ giác BMCD có:

N là trung điểm của BC (gt)

N là trung điểm của DM (gt)

\(\Rightarrow\) BMCD là hình bình hành

b) Để BMCD là hình thoi thì \(BC\perp DM\)

Ta có:

M là trung điểm của AC (gt)

N là trung điểm của BC (gt)

\(\Rightarrow MN\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow MN\) // \(AB\)

\(\Rightarrow DM\) // \(AB\)

Mà \(DM\perp BC\)

\(\Rightarrow BC\perp AB\)

Vậy để BMCD là hình thoi thì \(\Delta ABC\) vuông tại B

MN//PQ (cạnh đối hbh) => MI//KQ

Ta có

\(MI=\dfrac{MN}{2};KQ=\dfrac{PQ}{2}\) Mà MN=PQ (cạnh đối hbh) => MI=KQ

=> MIKQ là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

b/

Ta có

MA=MQ (gt) (1)

\(MN=2MQ\left(gt\right)\Rightarrow MQ=\dfrac{MN}{2}\) (2)

Ta có

\(MI=\dfrac{MN}{2}\) (3)

Từ (1) (2) (3) \(\Rightarrow MA=MI=\dfrac{MN}{2}\) => tg AMI cân tại M

Ta có

\(\widehat{AMI}=\widehat{AMP}-\widehat{M}=180^o-120^o=60^o\)

Xét tg AMI có

\(\widehat{MAI}+\widehat{MIA}+\widehat{AMI}=180^o\)

\(\Rightarrow\widehat{MAI}+\widehat{MIA}=180^o-\widehat{AMI}=180^o-60^o=120^o\)

Mà \(\widehat{MAI}=\widehat{MIA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\dfrac{120^o}{2}=60^o\)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\widehat{AMI}=60^o\Rightarrow\Delta AMI\) là tg đều

c/

Xét hbh MNPQ có

MQ//NP => MA//NP

MA=MQ (gt); MQ=NP (cạnh đối hbh)

=> MA=NP

=> APMN là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

Ta có

\(MI=AI=\dfrac{MN}{2}\)  (cạnh tg đều)

\(NI=\dfrac{MN}{2}\)

\(\Rightarrow AI=NI=\dfrac{MN}{2}\) => tg AIN cân tại I

Ta có \(\widehat{AIN}=\widehat{MIN}-\widehat{AIM}=180^o-60^o=120^o\)

Xét tg cân AIN có

\(\widehat{AIN}+\widehat{IAN}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{IAN}+\widehat{INA}=180^o-\widehat{AIN}=180^o-120^o=60^o\)

Mà \(\widehat{IAN}=\widehat{INA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{IAN}=\widehat{INA}=\dfrac{60^o}{2}=30^o\)

Xét tg AMN có

\(\widehat{MAN}+\widehat{AMI}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{MAN}=180^o-\widehat{AMI}-\widehat{INA}=180^o-60^o-30^o=90^o\)

=> APMN là hình chữ nhật (hình bình hành có 1 góc vuông là HCN

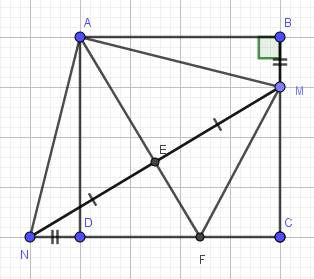
a) Do ABCD là hình vuông (gt)

\(\Rightarrow AB=AD\)

\(\widehat{ABM}=\widehat{ADN}=90^0\)

Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:

\(AB=AD\left(cmt\right)\)

\(BM=DN\left(gt\right)\)

\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)

\(\Rightarrow AM=AN\) (hai cạnh tương ứng)

\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)

Ta có:

\(\widehat{BAM}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{MAN}=90^0\)

\(\Delta AMN\) có:

\(AM=AN\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) cân tại A

Mà \(\widehat{MAN}=90^0\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) vuông cân tại A

b) Do \(\Delta AMN\) cân tại A

E là trung điểm của MN

\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)

\(\Rightarrow AE\perp MN\)

\(\Rightarrow EF\perp MN\)

Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:

\(EM=EN\left(gt\right)\)

\(EF\) là cạnh chung

\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)

\(\Rightarrow FM=FN\) (hai cạnh tương ứng)

Xét \(\Delta FAN\) và \(\Delta FAM\) có:

\(FA\) là cạnh chung

\(FN=FM\left(cmt\right)\)

\(AN=AM\left(cmt\right)\)

\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)

Câu 1: Nam làm bài kiểm tra có một số câu hỏi. Các câu hỏi có điểm bằng nhau. Nam trả lời sai 10 câu và được 60% tổng số điểm. Hỏi bài kiểm tra có bao nhiêu câu?

Câu 2. Nam vừa đứng thứ 15 từ dưới lên vừa đứng thứ 15 từ trên xuống trong cuộc thi đấu cầu lông. Hỏi có bao nhiêu người tham gia thi đấu?

Câu 3. Số nào tiếp theo dãy số sau?

135; 45; 180; 60; 240; 80; ...?...; 105

Câu 4. Chọn một hình a,b, c, d hoặc e để điền vào dấu (?)

Câu 9.

Chọn một hình a, b, c d hoc ede đen vào đầu (2),

Câu 5. Ở một vương quốc nọ có một nàng công chúa xinh đẹp, nên có nhiều chàng trai khôi ngô tuấn tú đến xin cưới nàng cùng một lúc. Vì họ đều giàu sang như nhau nên vua cha mới đưa ra một tình thế sau:

Vua đưa công chúa lên một tháp cao vút và bảo rằng, nếu chàng trai nào trả lời cho vua biết có bao nhiêu bậc thang dẫn đến chỗ công chúa thì sẽ cho cử hành hôn lễ ngay. Vua cho các chàng trai biết một vài số liệu: số bậc thang nhiều hơn 100 và ít hơn 120. nếu lính cánh bước một lần 3 bậc sẽ còn thừa một bậc, nếu bước một lần 4 bậc thì sẽ thừa 2, nếu bước 5 bậc sẽ còn thừa 3.

Vậy sẽ có ba

o nhiêu bậc thang?

Giúp mik với đh cần lập tức í ik mà mn ...

Ta có \(A=-x^2+2xy-4y^2+2x+10y-3\) 

\(A=-x^2+2\left(y+1\right)x-4y^2+10y-3\)

\(A=-x^2+2\left(y+1\right)x-\left(y+1\right)^2-3y^2+12y-2\)

\(A=-\left[x-\left(y+1\right)\right]^2-3\left(y^2-4y+4\right)+10\)

\(A=-\left(x-\left(y+1\right)\right)^2-3\left(y-2\right)^2+10\) \(\le10\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=y+1\\y-2=0\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(3,2\right)\)

Vậy \(max_A=10\)

?

x - y = 2 => x = y + 2 thay vào bt C, ta đc :

C = 2(y+2)^2 - y

= 2(y^2 + 4y + 4) - y

= 2(y^2 + 7/2 .y + 2)

= 2(y+7/4)^2 - 17/8 ≥ -17/8

=> Min = -17/8 tại y = -7/4, x =1/4

giúp mình bài này với

Đề bài là gì vậy bạn?