X/0,9=5/6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
24 tháng 3
Đúng(0)
24 tháng 3
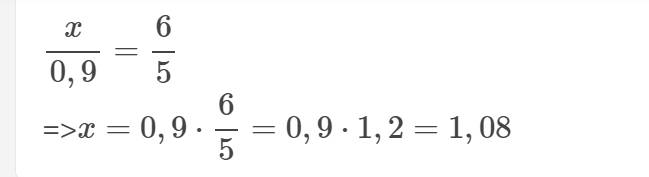
\(\dfrac{x}{0,9}=\dfrac{6}{5}\)
=>\(x=0,9\cdot\dfrac{6}{5}=0,9\cdot1,2=1,08\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
24 tháng 3
\(\dfrac{x}{0,9}\) = \(\dfrac{6}{5}\)
\(x\) = \(\dfrac{6}{5}\) x 0,9
\(x\) = 1,08
Vậy \(x=1,08\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
24 tháng 3
Tam giác cân là tam giác có hai cạnh bên bằng nhau.
TT
2
24 tháng 3
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của đoạn thẳng đó
24 tháng 3
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng ấy.
24 tháng 3
Gọi I là giao điểm của BM và CN, IK là phân giác của góc BIC(\(K\in BC\))
BM là phân giác của góc ABC
=>\(\widehat{ABM}=\widehat{CBM}=\dfrac{\widehat{ABC}}{2}\)
CN là phân giác của góc ACB
=>\(\widehat{ACN}=\widehat{NCB}=\dfrac{\widehat{ACB}}{2}\)
Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)+60^0=180^0\)
=>\(2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=120^0\)
=>\(\widehat{IBC}+\widehat{ICB}=60^0\)
Xét ΔBIC có \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)
=>\(\widehat{BIC}+60^0=180^0\)
=>\(\widehat{BIC}=120^0\)
Ta có: \(\widehat{NIB}+\widehat{BIC}=180^0\)(hai góc kề bù)
=>\(\widehat{NIB}+120^0=180^0\)
=>\(\widehat{NIB}=60^0\)
mà \(\widehat{NIB}=\widehat{MIC}\)(hai góc kề bù)
nên \(\widehat{MIC}=60^0\)
Ta có: IK là phân giác của góc BIC
=>\(\widehat{BIK}=\widehat{CIK}=\dfrac{\widehat{BIC}}{2}=60^0\)
Xét ΔBNI và ΔBKI có
\(\widehat{NIB}=\widehat{KIB}\left(=60^0\right)\)
IB chung
\(\widehat{NBI}=\widehat{KBI}\)
Do đó: ΔBNI=ΔBKI
=>BN=BK
Xét ΔCKI và ΔCMI có
\(\widehat{KIC}=\widehat{MIC}\left(=60^0\right)\)
IC chung
\(\widehat{KCI}=\widehat{MCI}\)
Do đó: ΔCKI=ΔCMI
=>CK=CM
Ta có: BN+CM
=BK+CK
=BC
VN
ai giải đúng và chi tiết nhất thì mik sẽ tik cho nhe
1
24 tháng 3
Câu 10:B
Câu 11: C
Câu 12: A
II: Tự luận
Bài 1:
\(\dfrac{-4}{5}=\dfrac{11}{2x-7}\)
=>\(2x-7=\dfrac{11\cdot5}{-4}=\dfrac{-55}{4}\)
=>\(2x=-\dfrac{55}{4}+7=\dfrac{-27}{4}\)
=>\(x=-\dfrac{27}{4}:2=-\dfrac{27}{8}\)
bài 3:
Số tiền cần trả khi mua 12 quyển tập là:
\(200000:20\cdot12=120000\left(đồng\right)\)
Bài 5:
a: Xét ΔCAD và ΔCED có
CA=CE
\(\widehat{ACD}=\widehat{ECD}\)
CD chung
Do đó: ΔCAD=ΔCED
=>DA=DE
b: Ta có: CA=CE
=>C nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra CD là đường trung trực của AE
=>CD\(\perp\)AE
c: Xét ΔDAE có DA=DE
nên ΔDAE cân tại D
24 tháng 3
a: Xét ΔMNP có MN<MP
mà \(\widehat{MPN};\widehat{MNP}\) lần lượt là góc đối diện của cạnh MN,MP
nên \(\widehat{MPN}< \widehat{MNP}\)
b: Xét ΔMNP vuông tại M và ΔMEP vuông tại M có
MN=ME
MP chung
Do đó: ΔMNP=ΔMEP
c: Xét ΔPEN có
PM,NH là các đường trung tuyến
PM cắt NH tại G
Do đó: G là trọng tâm của ΔPEN
=>\(PG=\dfrac{2}{3}PM=\dfrac{2}{3}\cdot12=8\left(cm\right)\)
24 tháng 3
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
b: Ta có: ΔBAE=ΔBHE
=>BA=BH và EA=EH
BA=BH nên B nằm trên đường trung trực của AH(1)
EA=EH nên E nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c: Ta có: EA=EH
EA<EK(ΔEAK vuông tại A)
Do đó: EH<EK
d: Xét ΔBKC có
KH,CA là các đường cao
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC
=>BE\(\perp\)KC