Chim ruồi "khổng lồ" Nam Mỹ là loại chim ruồi to nhất thế giới. Nó dài gấp 4 và 1/8 lần chim ruồi ong. Nếu độ dài chim ruồi ong là 5,5cm thì độ dài của chim ruồi khổng lồ Nam Mỹ là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: \(AB=\dfrac{BC}{2}\)
\(BE=EC=\dfrac{BC}{2}\)
Do đó: AB=BE=EC
Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
=>\(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
c: Xét ΔDBC có
DE là đường cao
DE là đường trung tuyến
Do đó: ΔDBC cân tại D
=>DB=DC
d: ΔDBC cân tại D
=>\(\widehat{DBC}=\widehat{DCB}\)
mà \(\widehat{ABC}=2\cdot\widehat{DBC}\)(BD là phân giác của góc ABC)
nên \(\widehat{ABC}=2\cdot\widehat{ACB}\)
ΔABC vuông tại A
=>\(2\cdot\widehat{ACB}+\widehat{C}=90^0\)
=>\(3\cdot\widehat{C}=90^0\)
=>\(\widehat{C}=\dfrac{90^0}{3}=30^0\)
\(\widehat{B}=2\cdot30^0=60^0\)


Thể tích phần bể chứa nước ban đầu là:
\(80\cdot50\cdot35=140000\left(cm^3\right)\)
Thể tích phần bể chứa nước lúc này sau khi thêm hòn đá là:
\(140000+20000=160000\left(cm^3\right)\)
Mực nước trong bể lúc này cao là:
\(160000:80:50=40\left(cm\right)\)
Thể tích ban đầu: 80 x 50 x 35 = 140.000 cm3
Sau khi thêm hòn đá: 140.000+20.000 = 160.000 cm3
=> Chiều cao mực nước = 160.000 / (80x50) = 40 cm

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+2⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+5⋮\sqrt{x}-3\)
=>\(5⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;5;-5\right\}\)
=>\(\sqrt{x}\in\left\{4;2;8\right\}\)
=>\(x\in\left\{16;4;64\right\}\)

Bài 5:
a: \(\left|-\dfrac{3}{5}+\dfrac{1}{2}\right|-\left(\dfrac{3}{4}-\dfrac{5}{8}\right)+\left|-\dfrac{3}{2}\right|\)
\(=\left|-\dfrac{6}{10}+\dfrac{5}{10}\right|-\dfrac{1}{8}+\dfrac{3}{2}\)
\(=\dfrac{1}{10}-\dfrac{1}{8}+\dfrac{3}{2}=\dfrac{4}{40}-\dfrac{5}{40}+\dfrac{60}{40}=\dfrac{59}{40}\)
b: \(\dfrac{2}{3}-\left|-\dfrac{7}{3}+\dfrac{3}{4}\right|-\left|-\dfrac{5}{2}+1\right|\)
\(=\dfrac{2}{3}-\left|-\dfrac{28}{12}+\dfrac{9}{12}\right|-\left|-\dfrac{5}{2}+\dfrac{2}{2}\right|\)
\(=\dfrac{2}{3}-\dfrac{19}{12}-\dfrac{3}{2}=\dfrac{8}{12}-\dfrac{19}{12}-\dfrac{18}{12}\)
\(=-\dfrac{29}{12}\)
c: \(\dfrac{1}{5}-\left(\dfrac{3}{10}-\dfrac{-3}{5}\right)-\left|\dfrac{1}{4}-\dfrac{2}{5}\right|\)
\(=\dfrac{1}{5}-\dfrac{3}{10}-\dfrac{3}{5}-\left|\dfrac{5}{20}-\dfrac{8}{20}\right|\)
\(=-\dfrac{7}{10}-\left|\dfrac{-3}{20}\right|=-\dfrac{7}{10}-\dfrac{3}{20}=-\dfrac{17}{20}\)
d: \(\left|-\dfrac{5}{2}+\dfrac{3}{4}-\dfrac{1}{3}\right|-\left(-\dfrac{3}{4}+\dfrac{-5}{3}\right)\)
\(=\left|-\dfrac{30}{12}+\dfrac{9}{12}-\dfrac{4}{12}\right|+\dfrac{3}{4}+\dfrac{5}{3}\)
\(=\dfrac{25}{12}+\dfrac{9}{12}+\dfrac{20}{12}=\dfrac{54}{12}=\dfrac{9}{2}\)

Bài 6:
a: \(\left|x+\dfrac{1}{2}\right|>=0\forall x;\left|y-\dfrac{3}{4}\right|>=0\forall y;\left|z-1\right|>=0\forall z\)
Do đó: \(\left|x+\dfrac{1}{2}\right|+\left|y-\dfrac{3}{4}\right|+\left|z-1\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+\dfrac{1}{2}=0\\y-\dfrac{3}{4}=0\\z-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{3}{4}\\z=1\end{matrix}\right.\)
b: \(\left|x-\dfrac{3}{4}\right|>=0\forall x;\left|\dfrac{2}{5}-y\right|>=0\forall y;\left|x-y+z\right|>=0\forall x,y,z\)
Do đó: \(\left|x-\dfrac{3}{4}\right|+\left|\dfrac{2}{5}-y\right|+\left|x-y+z\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{3}{4}=0\\\dfrac{2}{5}-y=0\\x-y+z=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{4}\\y=\dfrac{2}{5}\\z=-x+y=-\dfrac{3}{4}+\dfrac{2}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{4}\\y=\dfrac{2}{5}\\z=-\dfrac{7}{20}\end{matrix}\right.\)
c: \(\left|x-\dfrac{2}{3}\right|>=0\forall x;\left|x+y+\dfrac{3}{4}\right|>=0\forall x,y;\left|y-z-\dfrac{5}{6}\right|>=0\forall y,z\)
Do đó: \(\left|x-\dfrac{2}{3}\right|+\left|x+y+\dfrac{3}{4}\right|+\left|y-z-\dfrac{5}{6}\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{2}{3}=0\\x+y+\dfrac{3}{4}=0\\y-z-\dfrac{5}{6}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-x-\dfrac{3}{4}=-\dfrac{2}{3}-\dfrac{3}{4}\\z=y-\dfrac{5}{6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-\dfrac{17}{12}\\z=-\dfrac{17}{12}-\dfrac{10}{12}=-\dfrac{27}{12}=-\dfrac{9}{4}\end{matrix}\right.\)

Ta có: AB//DC
=>\(\widehat{A_1}=\widehat{D_4}\)(hai góc so le trong)
=>\(\widehat{D_4}=110^0\)
Ta có: \(\widehat{D_1}=\widehat{D_4}\)(hai góc đối đỉnh)
mà \(\widehat{D_4}=110^0\)
nên \(\widehat{D_1}=110^0\)
Ta có: AB//DC
=>\(\widehat{C_3}=\widehat{B_2}\)(hai góc so le trong)
=>\(\widehat{B_2}=135^0\)
Ta có: \(\widehat{B_1}+\widehat{B_2}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}=180^0-135^0=45^0\)
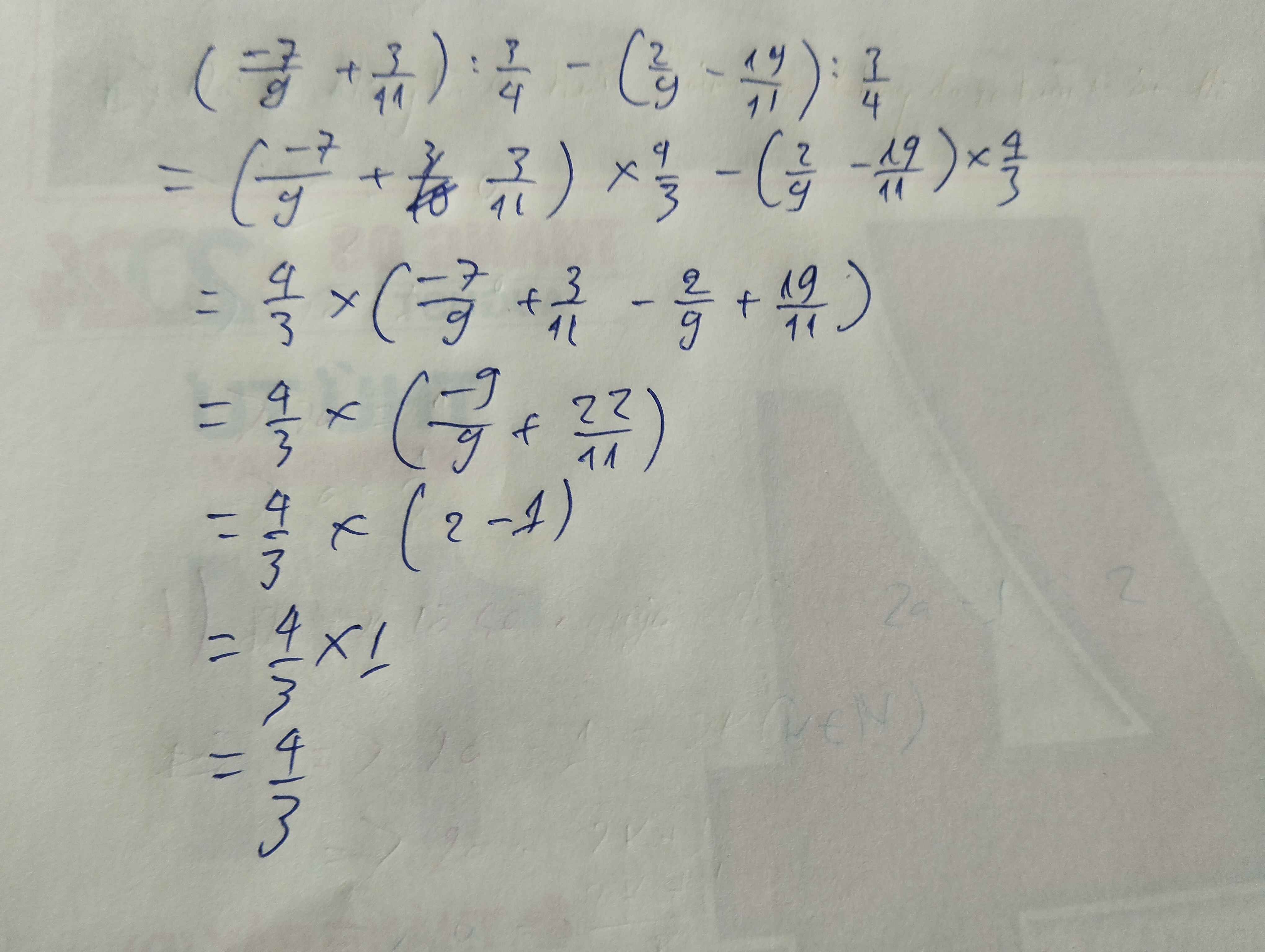
 giúp em bài 5 vs ạ
giúp em bài 5 vs ạ  giúp em bài 6 vs ạ
giúp em bài 6 vs ạ
= 388
Độ dài của chim ruồi khổng lồ Nam Mỹ là:
\(5,5\cdot\left(4\dfrac{1}{8}\right)=5,5\cdot4,125=\dfrac{363}{16}\left(cm\right)\)