
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(-3x\left(x-5\right)+5\left(x-1\right)+3x^2=4-x\\ \Rightarrow-3x^2+15x+5x-5+3x^2=4-x\\ \Rightarrow-3x^2+15x+5x+3x^2+x=4+5\\ \Rightarrow21x=9\\ \Rightarrow x=\dfrac{21}{9}.\)

Do f(2) = 6
⇒ 2² - 2b + 4 = 6
8 - 2b = 6
2b = 8 - 6
2b = 2
b = 2 : 2
b = 1
Vậy khi f(2) = 6 thì b = 1
Do f(2) = 6
⇒ 2² - 2b + 4 = 6
8 - 2b = 6
2b = 8 - 6
2b = 2
b = 2 : 2
b = 1
Vậy khi f(2) = 6 thì b = 1

\(E=\left(2-x\right)\left(1+2x\right)+\left(1+x\right)-\left(x^4+x^3-5x^2-5\right)\)
\(=2+4x-x-2x^2+1+x-x^4-x^3+5x^2+5\)
\(=-x^4-x^3+\left(-2x^2+5x^2\right)+\left(4x-x+x\right)+\left(2+1+5\right)\)
\(=-x^4-x^3+3x+4x+8\)
--------
\(G=\left(x^2-7\right)\left(x+2\right)-\left(2x-1\right)\left(x-14\right)+x\left(x^2-2x-22\right)+35\)
\(=x^3+2x^2-7x-14-2x^2+28x+x-14+x^2-2x^2-22x+35\)
\(=x^3+\left(2x^2-2x^2+x^2-2x^2\right)+\left(-7x+28x+x-22x\right)+\left(-14-14+35\right)\)
\(=x^3-x^2+7\)
--------
\(D=\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(x+5\right)-6\left(3x-2\right)\)
\(=6x^2+21x-2x-7-x^2-5x-x-5-18x+12\)
\(=\left(6x^2-x^2\right)+\left(21x-2x-5x-x-18x\right)+\left(-7-5+12\right)\)
\(=5x^2-5x\)
\(E=\left(2-x\right)\left(1+2x\right)+\left(1+x\right)-\left(x^4+x^3-5x^2-5\right)\)
\(=2+4x-x-2x^2+1+x-x^4-x^3+5x^2+5\)
\(=-x^4-x^3+3x^2+4x+8\)
\(G=\left(x^2-7\right)\left(x+2\right)-\left(2x-1\right)\left(x-14\right)+x\left(x^2-2x-22\right)+35\)
\(=x^3+2x^2-7x-14-\left(2x^2-28x-x+14\right)+x^3-2x^2-22x+35\)
\(=2x^3-29x+21-2x^2+29x-14\)
\(=2x^3-2x^2+7\)
\(D=\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(x+5\right)-6\left(3x-2\right)\)
\(=6x^2+21x-2x-7-\left(x^2+6x+5\right)-18x+12\)
\(=6x^2+x+12-x^2-6x-5=5x^2-5x+7\)

Gọi số lần xuất hiện mặt 4 chấm;5 chấm;6 chấm lần lượt là a(lần),b(lần),c(lần)
(Điều kiện: \(a,b,c\in Z^+\))
Số lần xuất hiện mặt 4 chấm bằng 2/3 lần số lần xuất hiện mặt 5 chấm
=>\(\dfrac{a}{2}=\dfrac{b}{3}\)
Số lần xuất hiện mặt 5 chấm bằng 60% số lần xuất hiện mặt 6 chấm
=>\(\dfrac{b}{3}=\dfrac{c}{5}\)
=>\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}\)
Tổng số lần xuất hiện mặt 4 chấm;5 chấm; 6 chấm là:
a+b+c=100-15-17-18=50
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{a+b+c}{2+3+5}=\dfrac{50}{10}=5\)
=>\(a=2\cdot5=10;b=3\cdot5=15;c=5\cdot5=25\)
Do đó: số lần xuất hiện mặt 4 chấm;5 chấm;6 chấm lần lượt là 10 lần; 15 lần; 25 lần
Số lần số chấm xuất hiện là số lẻ là:
15+15+18=48(lần)
=>Xác suất thực nghiệm là \(\dfrac{48}{100}=\dfrac{12}{25}\)

Ta có:
Q(x) = x² + 4x + 9
= x² + 2x + 2x + 4 + 5
= (x² + 2x) + (2x + 4) + 5
= x(x + 2) + 2(x + 2) + 5
= (x + 2)(x + 2) + 5
= (x + 2)² + 5
Do (x + 2)² ≥ 0 với mọi x ∈ R
⇒ (x + 2)² + 5 > 0 với mọi x ∈ R
Vậy Q(x) vô nghiệm

Do 1 > 0
\(\left|x\right|\ge0\)
\(\Rightarrow1+\left|x\right|>0\)
Do đó \(1+\left|x\right|=-2\) là điều vô lý
\(\Rightarrow\) Không tìm được \(x\) trong trường hợp này
Vậy bài của em là sai
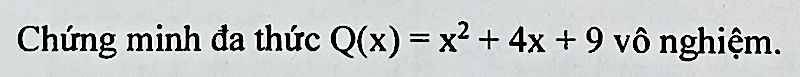


a: Xét ΔAHB và ΔAHC có
AB=AC
\(\widehat{BAH}=\widehat{CAH}\)
AH chung
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔAHB=ΔAHC
=>HB=HC
Xét ΔHKB vuông tại K và ΔHIC vuông tại I có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHKB=ΔHIC
=>BK=CI
c: Ta có: AK+KB=AB
AI+IC=AC
mà KB=IC và AB=AC
nên AK=AI
Xét ΔAIN vuông tại I và ΔAKM vuông tại K có
AI=AK
\(\widehat{IAN}\) chung
do đó: ΔAIN=ΔAKM
=>IN=KM
Xét ΔKAM vuông tại K có AM là cạnh huyền
nên AM là cạnh lớn nhất trong ΔKAM
=>AM>KM
=>\(\dfrac{1}{2}\left(KM+KM\right)< AM\)
=>\(\dfrac{1}{2}\left(KM+IN\right)< AM\)