tìm tất cả các số nguyên x thỏa mãn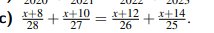
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


"BSĐ: tìm nghiệm nguyên"
`x+2y+xy=5`
`=>x+y(x+2)=5`
`=>(x+2)+y(x+2)=5+2`
`=>(x+2)(y+1)=7`
Ta có bảng:
| x + 2 | 1 | 7 | -1 | -7 |
| y + 1 | 7 | 1 | -7 | -1 |
| x | -1 | 5 | -3 | -9 |
| y | 6 | 0 | -8 | -2 |
Vậy: ..
nếu (x=1):[1+2y+1/cdot y=5] [1+2y+y=5] [1+3y=5] [3y=4] [y=\frac{4}{3}]
Vậy là (x=1) và (y=\frac{4}{3})
bạn xem có đúng ko nhé

a: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(30^0< 100^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
=>\(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
=>\(\widehat{yOz}=100^0-30^0=70^0\)
Vì tia Ot nằm trong góc yOz
nên tia Ot nằm giữa hai tia Oy,Oz
=>\(\widehat{yOt}+\widehat{zOt}=\widehat{yOz}\)
=>\(\widehat{zOt}=70^0-20^0=50^0\)
Vì \(\widehat{yOt}< \widehat{zOt}\left(20^0< 50^0\right)\)
nên Ot không là phân giác của góc yOz
b: Vì \(\widehat{zOt}< \widehat{zOx}\left(50^0< 100^0\right)\)
nên tia Ot nằm giữa hai tia Oz và Ox
=>\(\widehat{tOz}+\widehat{tOx}=\widehat{xOz}\)
=>\(\widehat{xOt}=100^0-50^0=50^0\)
Ta có: tia Ot nằm giữa hai tia Ox và Oz
mà \(\widehat{xOt}=\widehat{zOt}\left(=50^0\right)\)
nên Ot là phân giác của góc xOz

a: \(\left|x+\dfrac{1}{2}\right|>=0\forall x\)
Dấu '=' xảy ra khi \(x+\dfrac{1}{2}=0\)
=>\(x=-\dfrac{1}{2}\)
b: \(\left|x-\dfrac{1}{3}\right|>=0\forall x\)
=>\(\left|x-\dfrac{1}{3}\right|+2>=2\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{3}=0\)
=>\(x=\dfrac{1}{3}\)

Em ghi thế này thì cả C lẫn D đều sai
Đáp án C chắc là \(\widehat{A}=\widehat{C};\widehat{B}=\widehat{D}\) mà em ghi nhầm

Thêm điều kiện: `x;y in Z`
Do `x;y in Z`
`=> x-1 in Z và y+1 in Z`
Mà `(x-1)(y+1)=3`
`=> x - 1 in Ư(3) = {-3;-1;1;3}`
`=> x in {-2;0;2;4} `
Khi đó: `y + 1 in {-1;-3;3;1}`
`=> y in {-2;-4;2;0}` (Thỏa mãn)
Vậy `(x;y) in {(-2;-2);(0;-4);(2;2);(4;0)}`
Bài 2:Tìm các số x,y,z biết:
\(\dfrac{x-1}{2}\)=\(\dfrac{y+3}{4}\)=\(\dfrac{z-5}{6}\) và 5z-3x-4y=50

Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}=\dfrac{-3\left(x-1\right)-4\left(y+3\right)+5\left(z-5\right)}{-3\cdot2-4\cdot4+5\cdot6}\\ =\dfrac{\left(5z-3x-4y\right)+\left(3-12-25\right)}{-6-16+30}=\dfrac{50-34}{8}=2\)
`=>(x-1)/2=2=>x-1=4=>x=5`
`=>(y+3)/4=2=>y+3=8=>y=5`
`=>(z-5)/6=2=>z-5=12=>z=17`

a) Căn bậc 2 số học của `121` là `11`
Căn bậc 2 của `121` là ` +-11`
b) Căn bậc 2 số học của `(-5/6)^2 ` là ` 5/6`
Căn bậc 2 của `(-5/6)^2` là ` +-5/6`

`A = (5m + n - 4)(9m - 11n + 1) `
- Xét m và n là số lẻ thì:
`5m` là số lẻ
`n` là số lẻ
`=> 5m + n` là số chẵn
`=> 5m + n - 4 ` là số chẵn
`=> A` chia hết 2
- Xét m và n là số chẵn thì:
`5m` là số chẵn
`n` là số chẵn
`=> 5m + n` là số chẵn
`=> 5m + n - 4 ` là số chẵn
`=> A` chia hết 2
- Xét m là số lẻ và n là số chẵn thì:
`9m` là số lẻ
`11n` là số chẵn
`=> 9m - 11n` là số lẻ
`=> 9m - 11n + 1` là số chẵn
`=> A` chia hết cho 2
- Xét m là số chẵn và n là số lẻ thì:
`9m` là số chẵn
`11n` là số lẻ
`=> 9m - 11n` là số lẻ
`=> 9m - 11n + 1 ` là số chẵn
`=> A` chia hết cho 2
Vậy với mọi số nguyên m và n thì A chia hết cho 2
Ta có:
\(\left(5m+n-4\right)+\left(9m-11n+1\right)=10m-10n-3=2\left(5m-5n\right)-3\) luôn là số lẻ với mọi m;n nguyên
\(\Rightarrow5m+n-4\) và \(9m-11n+1\) luôn khác tính chẵn lẻ với mọi m; n nguyên
\(\Rightarrow\) Trong 2 số luôn có 1 số lẻ và 1 số chẵn
\(\Rightarrow\) Tích của 2 số luôn là 1 số chẵn
\(\Rightarrow\) Tích của 2 số luôn chia hết cho 2 với mọi m;n nguyên

\(\dfrac{x+8}{28}+\dfrac{x+10}{27}=\dfrac{x+12}{26}+\dfrac{x+14}{25}\)
\(\left(\dfrac{x+8}{28}+2\right)+\left(\dfrac{x+10}{27}+2\right)=\left(\dfrac{x+12}{26}+2\right)+\left(\dfrac{x+14}{25}+2\right)\)
\(\dfrac{x+64}{28}+\dfrac{x+64}{27}=\dfrac{x+64}{26}+\dfrac{x+64}{25}\)
\(\dfrac{x+64}{28}+\dfrac{x+64}{27}-\dfrac{x+64}{26}-\dfrac{x+64}{25}=0\)
\(\left(x+64\right)\left(\dfrac{1}{28}+\dfrac{1}{27}-\dfrac{1}{26}-\dfrac{1}{25}\right)=0\)
\(x+64=0\) (do \(\dfrac{1}{28}+\dfrac{1}{27}-\dfrac{1}{26}-\dfrac{1}{25}\ne0\))
\(x=-64\)