1: Xét tứ giác ABCK có \(\widehat{BAC}=\widehat{BKC}=90^0\)

nên ABCK là tứ giác nội tiếp

2:

Xét ΔCKB vuông tại K và ΔCEF vuông tại E có

\(\widehat{KCB}\) chung

Do đó: ΔCKB~ΔCEF

=>\(\dfrac{CK}{CE}=\dfrac{CB}{CF}\)

=>\(CK\cdot CF=CB\cdot CE\)

Xét ΔACB vuông tại A có AE là đường cao

nên \(CE\cdot CB=CA^2\)

=>\(CA^2=CK\cdot CF\)

=>\(\dfrac{CA}{CF}=\dfrac{CK}{CA}\)

Xét ΔCAK và ΔCFA có

\(\dfrac{CA}{CF}=\dfrac{CK}{CA}\)

\(\widehat{ACK}\) chung

Do đó: ΔCAK~ΔCFA

1. Chứng minh tứ giác ABCK nội tiếp:
Ta có ∆ABC vuông tại A, do đó góc ACB là góc vuông.
Gọi H là trực tâm của ∆BFC, suy ra BH ⊥ FC.
Vì A là trung điểm của EF, AE = EF và AE ⊥ BC (vì AE là đường cao), suy ra E là trung điểm của BC.
Từ đó, BK cũng là đường cao của ∆BFC, suy ra BK ⊥ FC.
Vậy tứ giác ABCK có hai đường chéo AC và BK cùng vuông góc với cạnh BC, suy ra tứ giác ABCK nội tiếp đường tròn đường kính BC.
2. Chứng minh tam giác CAK đồng dạng với tam giác CFA:
Vì tứ giác ABCK nội tiếp, suy ra góc BAC = góc BKC (cùng chắn cung BC).
Góc BAC là góc vuông (vì ∆ABC vuông tại A), suy ra góc BKC cũng là góc vuông.
Do đó, ∆BKC vuông tại K.
Vì ∆ABC vuông tại A, suy ra góc ABC + góc BAC = 90°.
Tương tự, trong ∆BFC vuông tại F, ta có góc BFC + góc FBC = 90°.
Vì E là trung điểm của BC, suy ra BE = EC và góc ABC = góc FBC.
Từ đó, góc BAC = góc BKC và góc ABC = góc FBC, suy ra ∆CAK đồng dạng với ∆CFA theo trường hợp góc-góc.
3. Chứng minh H là trung điểm của AE:
Vì H là trực tâm của ∆BFC, suy ra BH ⊥ FC và CH ⊥ BF.
Vì BK là đường cao của ∆BFC, suy ra BK ⊥ FC.
Vì E là trung điểm của BC và AE ⊥ BC, suy ra AE là đường trung bình của ∆BFC.
Đường trung bình trong tam giác vuông cũng là đường cao, suy ra H là giao điểm của AE và BK.
Do đó, H chia AE thành hai đoạn bằng nhau, suy ra H là trung điểm của AE.

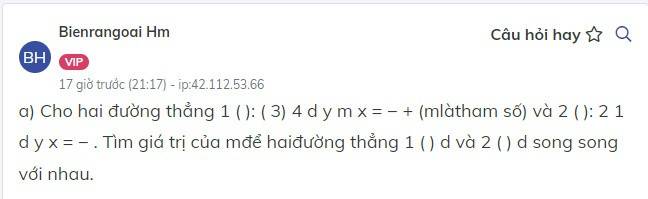
Có vẻ đề bài bị lỗi hiện thị em ạ, em xem lại nhé.

Lời giải:

ĐKXĐ: $x\geq 1$

PT $\Leftrightarrow \sqrt{(x-1)+8\sqrt{x-1}+16}+\sqrt{(x-1)+4\sqrt{x-1}+4}=6$

$\Leftrightarrow \sqrt{(\sqrt{x-1}+4)^2}+\sqrt{(\sqrt{x-1}+2)^2}=6$

$\Leftrightarrow |\sqrt{x-1}+4|+|\sqrt{x-1}+2|=6$

$\Leftrightarrow 2\sqrt{x-1}+6=6$

$\Leftrightarrow \sqrt{x-1}=0$

$\Leftrightarrow x-1=0$

$\Leftrightarrow x=1$ (tm)

\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left(m-1\right)\)

\(=4-4m+4=-4m+8\)

Để phương trình có hai nghiệm phân biệt thì Δ>0

=>-4m+8>0

=>-4m>-8

=>m<2

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)

\(x_1^2+x_2^2-3x_1x_2=2m^2+\left|m+3\right|\)

=>\(\left(x_1+x_2\right)^2-5x_1x_2=2m^2+\left|m+3\right|\)

=>\(2m^2+\left|m+3\right|=2^2-5\left(m-1\right)\)

=>\(2m^2+\left|m+3\right|=4-5m+5=-5m+9\)

=>\(2m^2+\left|m+3\right|+5m-9=0\)(1)

TH1: -3<=m<2

(1) sẽ trở thành \(2m^2+m+3+5m-9=0\)

=>\(2m^2+6m-6=0\)

=>\(m^2+3m-3=0\)

=>\(\left[{}\begin{matrix}m=\dfrac{-3+\sqrt{21}}{2}\left(nhận\right)\\m=\dfrac{-3-\sqrt{21}}{2}\left(loại\right)\end{matrix}\right.\)

TH2: m<-3

(1) sẽ trở thành \(2m^2-m-3+5m-9=0\)

=>\(2m^2+4m-12=0\)

=>\(m^2+2m-6=0\)

=>\(\left(m+1\right)^2=7\)

=>\(\left[{}\begin{matrix}m=\sqrt{7}-1\left(loại\right)\\x=-\sqrt{7}-1\left(nhận\right)\end{matrix}\right.\)

1: ΔOCD cân tại O

mà OI là đường trung tuyến

nên OI\(\perp\)CD

Xét tứ giác OIAM có \(\widehat{OIM}=\widehat{OAM}=90^0\)

nên OIAM là tứ giác nội tiếp

=>O,I,A,M cùng thuộc một đường tròn

2: ΔOAM vuông tại A

=>\(AO^2+AM^2=MO^2\)

=>\(AM^2=\left(\dfrac{3R}{2}\right)^2-R^2=\dfrac{5}{4}R^2\)

Xét (O) có

\(\widehat{MAC}\) là góc tạo bởi tiếp tuyến AM và dây cung AC

\(\widehat{ADC}\) là góc nội tiếp chắn cung AC

Do đó: \(\widehat{MAC}=\widehat{ADC}\)

Xét ΔMAC và ΔMDA có

\(\widehat{MAC}=\widehat{MDA}\)

\(\widehat{AMC}\) chung

Do đó: ΔMAC~ΔMDA

=>\(\dfrac{MA}{MD}=\dfrac{MC}{MA}\)

=>\(MC\cdot MD=MA^2=\dfrac{5}{4}R^2\)

Lời giải:
Gọi số kg nho và táo bác An mua lần lượt là $a$ và $b$ (kg). Theo bài ra ta có:

\(\left\{\begin{matrix} a+b=7\\ 65000a+50000b=410000\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a+b=7\\ 13a+10b=82\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=4\\ b=3\end{matrix}\right.\)

Vậy bác An mua 4 kg nho và 3 kg táo.