
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(0,5^{1000}=\left(0,5^5\right)^{200}=0,03125^{200}\)
mà \(0,03125< 0,625\)
nên \(0,5^{1000}< 0,625^{200}\)
c: \(A=2+2^2+...+2^{2022}\)
=>\(2A=2^2+2^3+...+2^{2023}\)
=>\(2A-A=2^2+2^3+...+2^{2023}-2-2^2-...-2^{2022}\)
=>\(A=2^{2023}-2\)
=>A<B
e: \(2020A=\dfrac{2020^{2024}-2020}{2020^{2024}-1}=1-\dfrac{2019}{2020^{2024}-1}\)
\(2020B=\dfrac{2020^{2024}+2020}{2020^{2024}+1}=1+\dfrac{2019}{2020^{2024}+1}\)
Vì \(-\dfrac{2019}{2020^{2024}-1}< 0< \dfrac{2019}{2020^{2024}+1}\)
nên \(-\dfrac{2019}{2020^{2024}-1}+1< \dfrac{2019}{2020^{2024}+1}+1\)
=>2020A<2020B
=>A<B
d: \(\left(-\dfrac{3}{2}\right)^{2024}=\left(\dfrac{3}{2}\right)^{2024};\left(-2\right)^{2024}=2^{2024}\)
mà 3/2<2
nên \(\left(-\dfrac{3}{2}\right)^{2024}< 2^{2024}\)

Để so sánh hai số 0.25 và 0.6, ta có thể sử dụng các cách sau:
1. So sánh trực tiếp:
Nhìn vào hai số, ta có thể thấy 0.6 lớn hơn 0.25.
2. Vẽ số trên trục số:
-
Vẽ trục số và đánh dấu các điểm 0, 0.25 và 0.6.
-
Qua hình vẽ, ta thấy điểm 0.6 nằm xa điểm 0 hơn so với điểm 0.25. Do đó, 0.6 lớn hơn 0.25.
3. Sử dụng biểu đồ số:
- Vẽ biểu đồ số với hai thanh có chiều cao tương ứng với 0.25 và 0.6. So sánh 0.25 và 0.6 bằng biểu đồ số
- Chiều cao của thanh 0.6 cao hơn so với thanh 0.25. Do đó, 0.6 lớn hơn 0.25.
Kết luận:
Bằng cả ba cách so sánh trên, ta có thể cho thấy: 0.6 lớn hơn 0.25.
Ngoài ra, ta cũng có thể sử dụng các phép toán sau để so sánh hai số:
- 0.6 - 0.25 = 0.35 > 0
- 0.25 / 0.6 = 0.4167 < 1
Cả hai phép toán này đều cho ta kết quả 0.6 lớn hơn 0.25.

x, y là 2 đại lượng tỉ lệ nghịch nên ta có: \(xy=k=>k=4\cdot1,5=6\)
\(x=0,5=>y=\dfrac{k}{x}=\dfrac{6}{0,5}=12\)
\(x=-1,2=>y=\dfrac{k}{x}=\dfrac{6}{-1,2}=-5\)
\(y=3=>x=\dfrac{k}{y}=\dfrac{6}{3}=2\)
\(y=-2=>x=\dfrac{k}{y}=\dfrac{6}{-2}=-3\)
| x | 0,5 | -1,2 | 2 | -3 | 4 |
| y | 12 | -5 | 3 | -2 | 1,5 |

x và y là 2 đại lượng tỉ lệ nghịch nên: \(xy=k=>k=-2\cdot-15=30\)
\(x=10=>y=\dfrac{k}{x}=\dfrac{30}{10}=3\)
\(y=-3=>x=\dfrac{30}{-3}=-10\)
\(x=15=>y=\dfrac{k}{x}=\dfrac{30}{15}=2\)
\(y=5=>x=\dfrac{k}{y}=\dfrac{30}{5}=6\)
| x | -2 | 10 | -10 | 15 | 6 |
| y | -15 | 3 | -3 | 2 | 5 |

\(\left[\left(-\dfrac{1}{2}\right)^3-\left(\dfrac{3}{4}\right)^3\cdot\left(-2\right)^2\right]:\left[2\cdot\left(-1\right)^5+\left(\dfrac{3}{4}\right)^2-\dfrac{3}{8}\right]\\ =\left(-\dfrac{1}{8}-\dfrac{27}{64}\cdot4\right):\left(2\cdot-1+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(-\dfrac{1}{8}-\dfrac{27}{16}\right):\left(-2+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(\dfrac{-2}{16}-\dfrac{27}{16}\right):\left(\dfrac{-32}{16}+\dfrac{9}{16}-\dfrac{6}{16}\right)\\ =\dfrac{-29}{16}:\dfrac{-29}{16}\\ =1\)
____________________________
\(\left[3\dfrac{1}{6}-\left(0,06\cdot7\dfrac{1}{2}+6\dfrac{1}{4}\cdot0,24\right)\right]:\left(1\dfrac{2}{3}+2\dfrac{2}{3}\cdot1\dfrac{3}{4}\right)\\ =\left[\dfrac{19}{6}-\left(0,06\cdot\dfrac{15}{2}+\dfrac{25}{4}\cdot4\cdot0,06\right)\right]:\left(\dfrac{5}{3}+\dfrac{8}{3}\cdot\dfrac{7}{4}\right)\\ =\left[\dfrac{19}{6}-0,06\cdot\left(\dfrac{15}{4}+25\right)\right]:\left(\dfrac{5}{3}+\dfrac{14}{3}\right)\\ =\left(\dfrac{19}{6}-0,06\cdot\dfrac{65}{2}\right):\dfrac{19}{3}\\ =\left(\dfrac{19}{6}-\dfrac{39}{20}\right):\dfrac{19}{3}\\ =\dfrac{73}{60}:\dfrac{19}{3}\\ =\dfrac{73}{380}\)

Bài 1:
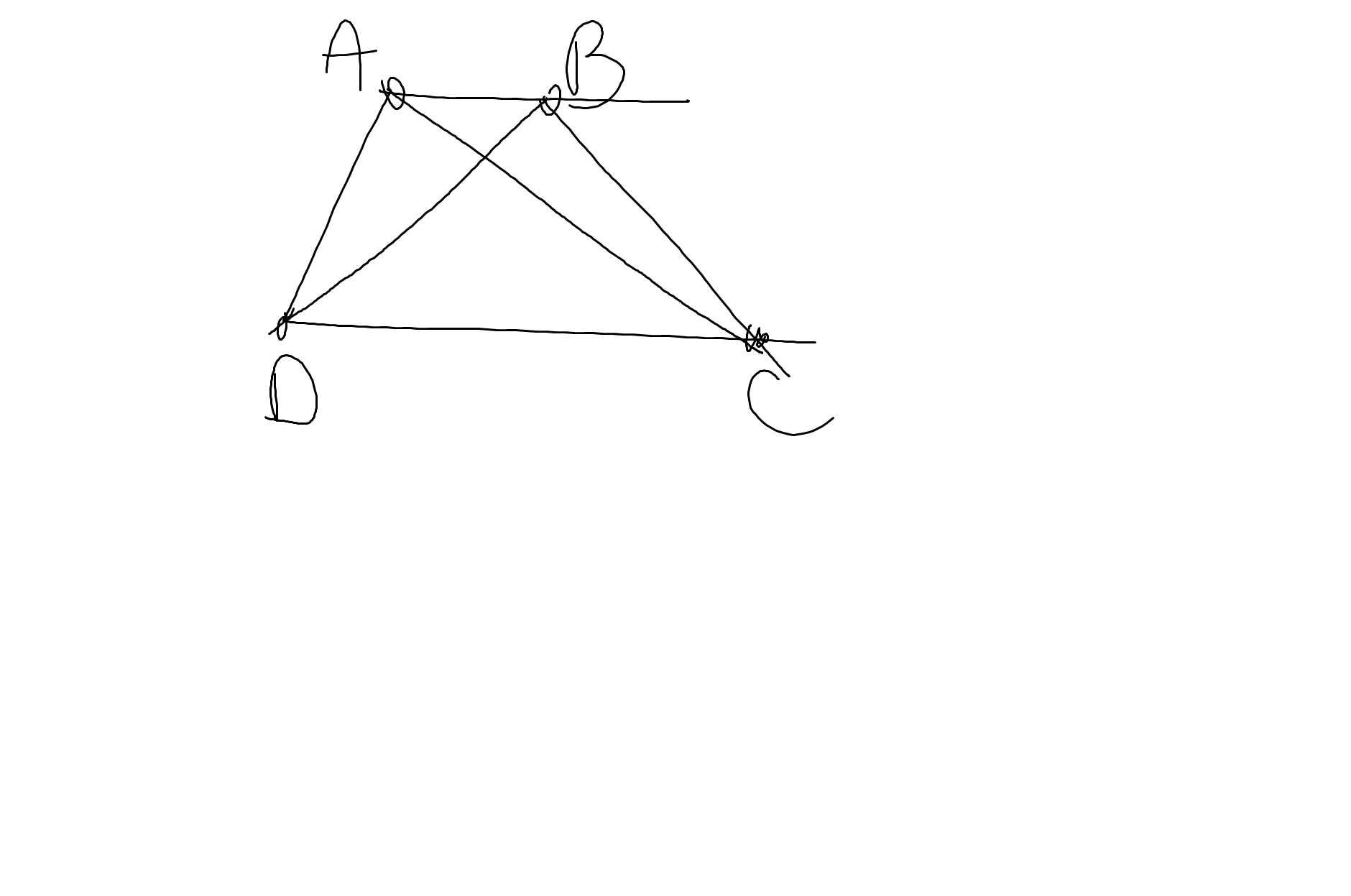
a: Hai cạnh đáy là AB,CD
Hai cạnh bên là AD,BC
b: Các cặp góc kề cạnh đáy là:
\(\widehat{BAD};\widehat{ABC}\)
\(\widehat{ADC};\widehat{BCD}\)
Các cặp góc kề cạnh bên là:
\(\widehat{BAD};\widehat{ADC}\)
\(\widehat{ABC};\widehat{BCD}\)
c: Hai đường chéo là AC,BD
Bài 2:
a: Ta có: ΔDAC vuông cân tại D
=>\(\widehat{DAC}=\widehat{DCA}=45^0\)
Ta có: ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
Ta có: \(\widehat{DAC}=\widehat{ACB}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//CB
=>ABCD là hình thang
Hình thang ABCD có AD\(\perp\)DC
nên ABCD là hình thang vuông
b: ABCD là hình thang vuông có hai đáy là AD,CB và AD\(\perp\)DC
=>CB\(\perp\)CD
=>\(\widehat{ADC}=\widehat{DCB}=90^0\)
Ta có: AD//CB
=>\(\widehat{DAB}+\widehat{ABC}=180^0\)
=>\(\widehat{DAB}=180^0-45^0=135^0\)

Bài 1:
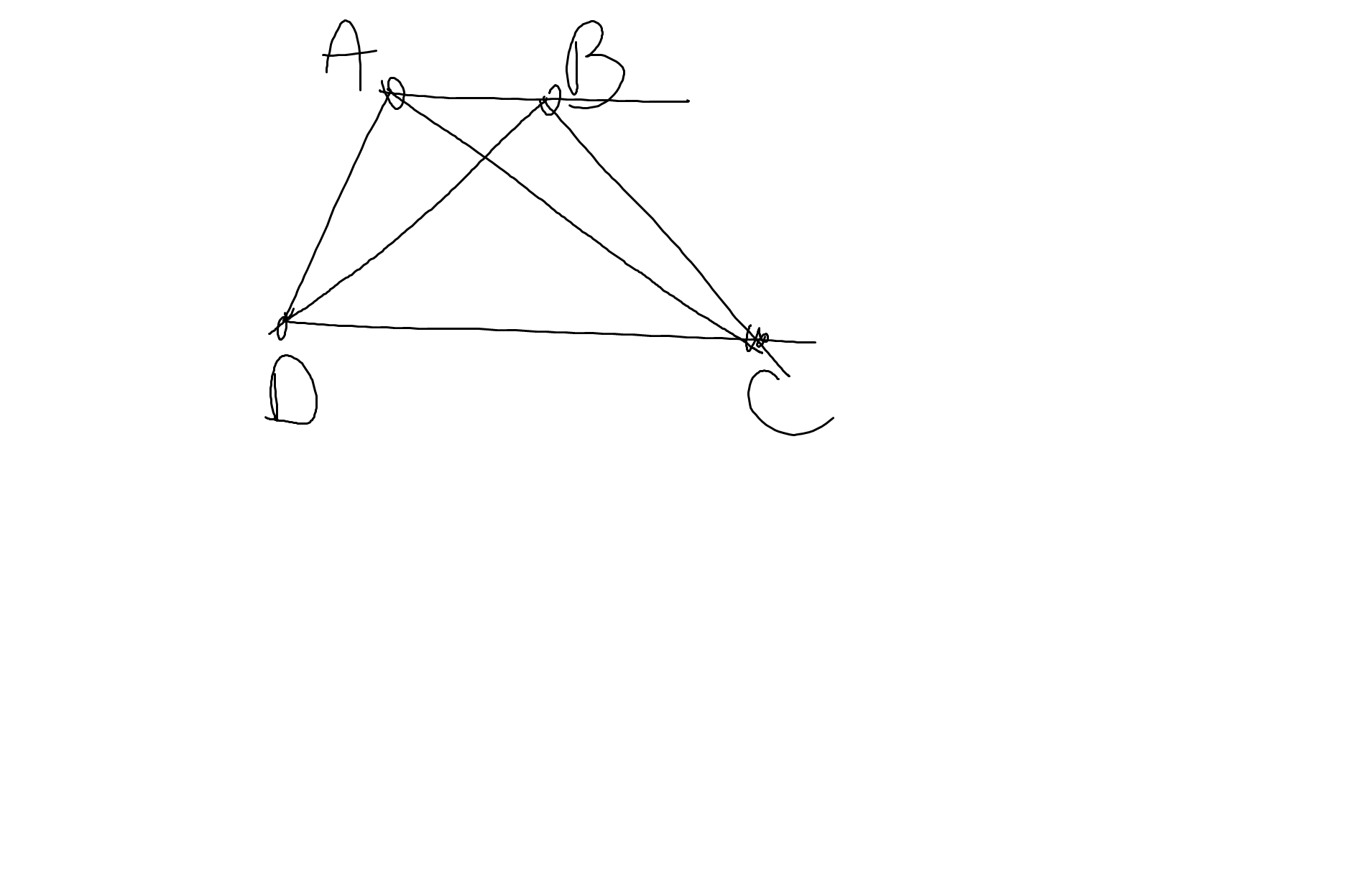
a: Hai cạnh đáy là AB,CD
Hai cạnh bên là AD,BC
b: Các cặp góc kề cạnh đáy là:
\(\widehat{BAD};\widehat{ABC}\)
\(\widehat{ADC};\widehat{BCD}\)
Các cặp góc kề cạnh bên là:
\(\widehat{BAD};\widehat{ADC}\)
\(\widehat{ABC};\widehat{BCD}\)
c: Hai đường chéo là AC,BD
Bài 2:
a: Ta có: ΔDAC vuông cân tại D
=>\(\widehat{DAC}=\widehat{DCA}=45^0\)
Ta có: ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
Ta có: \(\widehat{DAC}=\widehat{ACB}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//CB
=>ABCD là hình thang
Hình thang ABCD có AD\(\perp\)DC
nên ABCD là hình thang vuông
b: ABCD là hình thang vuông có hai đáy là AD,CB và AD\(\perp\)DC
=>CB\(\perp\)CD
=>\(\widehat{ADC}=\widehat{DCB}=90^0\)
Ta có: AD//CB
=>\(\widehat{DAB}+\widehat{ABC}=180^0\)
=>\(\widehat{DAB}=180^0-45^0=135^0\)

a)
\(\dfrac{8}{9}-\dfrac{1}{72}-\dfrac{1}{56}-\dfrac{1}{42}-\dfrac{1}{30}-\dfrac{1}{20}-\dfrac{1}{12}-\dfrac{1}{6}-\dfrac{1}{2}\\ =\dfrac{8}{9}-\left(\dfrac{1}{72}+\dfrac{1}{56}+\dfrac{1}{42}+\dfrac{1}{30}+\dfrac{1}{20}+\dfrac{1}{12}+\dfrac{1}{6}+\dfrac{1}{2}\right)\\ =\dfrac{8}{9}-\left(\dfrac{1}{8\cdot9}+\dfrac{1}{7\cdot8}+\dfrac{1}{6\cdot7}+\dfrac{1}{6\cdot5}+\dfrac{1}{4\cdot5}+\dfrac{1}{3\cdot4}+\dfrac{1}{2\cdot3}+\dfrac{1}{1\cdot2}\right)\\ =\dfrac{8}{9}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\right)\\ =\dfrac{8}{9}-\left(1-\dfrac{1}{9}\right)\\ =\dfrac{8}{9}-\dfrac{8}{9}\\ =0\)
b)
\(\left(-\dfrac{1}{2}\right)-\left(\dfrac{-3}{5}\right)+\left(-\dfrac{1}{9}\right)+\dfrac{1}{127}-\dfrac{7}{18}+\dfrac{4}{35}-\left(\dfrac{-2}{7}\right)\\ =\left(-\dfrac{1}{2}-\dfrac{1}{9}-\dfrac{7}{18}\right)+\left(\dfrac{3}{5}+\dfrac{2}{7}+\dfrac{4}{35}\right)+\dfrac{1}{127}\\ =\dfrac{-9-2-7}{18}+\dfrac{21+10+4}{35}+\dfrac{1}{127}\\ =-1+1+\dfrac{1}{127}\\ =\dfrac{1}{127}\)
c) (*sửa*)
\(\dfrac{3}{5}+\dfrac{3}{11}-\dfrac{-3}{7}+\dfrac{2}{97}-\dfrac{1}{35}-\dfrac{3}{4}-\dfrac{23}{44}\\ =\dfrac{3}{5}+\dfrac{3}{11}+\dfrac{3}{7}+\dfrac{2}{97}-\dfrac{1}{35}-\dfrac{3}{4}+\dfrac{23}{44}\\ =\left(\dfrac{3}{5}+\dfrac{3}{7}-\dfrac{1}{35}\right)+\left(\dfrac{3}{11}-\dfrac{3}{4}-\dfrac{23}{44}\right)+\dfrac{2}{97}\\ =\dfrac{21+15-1}{35}+\dfrac{12-33-23}{44}+\dfrac{2}{97}\\ =1+\left(-1\right)+\dfrac{2}{97}\\ =\dfrac{2}{97}\)
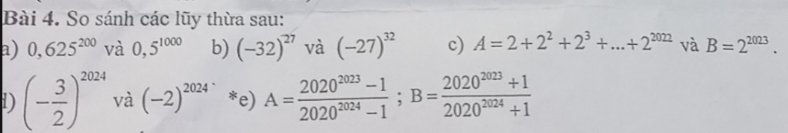
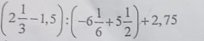


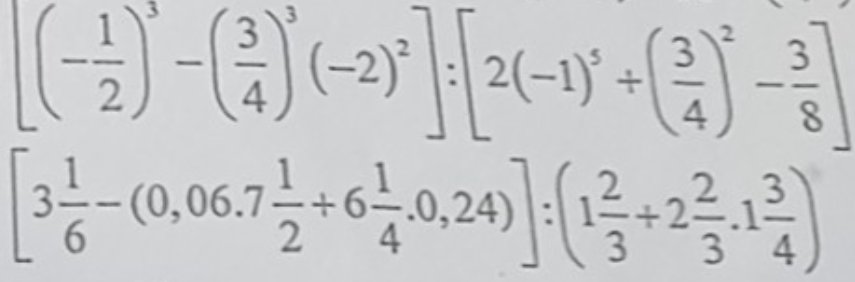

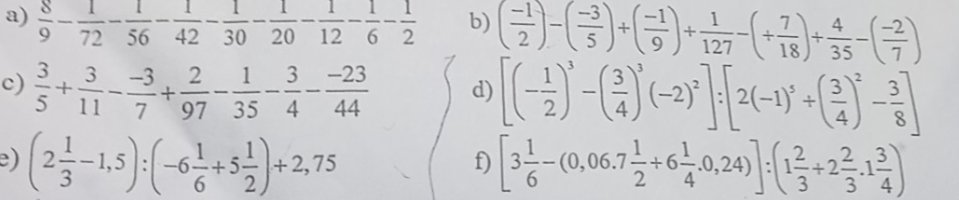
Số công nhân cần có để hoàn thành công việc trong 14 ngày là:
\(56\cdot\dfrac{21}{14}=56\cdot\dfrac{3}{2}=84\left(người\right)\)
Số công nhân cần tăng thêm là:
84-56=28(người)
Giải:
Một công nhân hoàn thành công việc đó trong số ngày là:
21 x 56 = 1176 (ngày)
Để hoàn thành công việc trong 14 ngày cần số người là:
1176 : 14 = 84 (người)
Vậy để hoàn thành công việc trong 14 ngày cần bổ sung thêm số người là:
84 - 56 = 28 (người)
Đáp số:.....