Cho tam giác \(ABC\) có ba góc ngọn, các điểm \(M\), \(N\) thứ tự là trung điểm của \(BC\) và \(AC\). Các đường trung trực của \(BC\) và \(AC\) cắt nhau tại \(O\). Qua \(A\) kẻ đường thẳng song song với \(OM\), qua \(B\) kẻ đường thẳng song song với \(ON\), chúng cắt nhau tại \(H\).
\(a.\) Nối \(MN\), \(\Delta AHB\) đồng dạng với tam giác nào?
\(b.\) Gọi \(G\) là trọng tâm \(\Delta ABC\), chứng minh \(\Delta AHG\) đồng dạng với \(\Delta MOG\)?
\(c.\) Chứng minh ba điểm \(H\), \(O\), \(G\) thẳng hàng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong △ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: (tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên
Suy ra: (tính chất tỉ lệ thức)
Suy ra:
Trong △ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: (tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên
Suy ra: (tính chất tỉ lệ thức)
Suy ra:

B C A x y D E O I J G
a/
\(\widehat{BAC}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow AB\perp AC\Rightarrow AI\perp AC\)
\(OE\perp AC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường thẳng nối điểm đó với tâm đường tròn vuông góc với đường thẳng nối hai tiếp điểm) \(\Rightarrow OJ\perp AC\)
=> AI//OJ (cùng vuông góc với AC) (1)
\(\widehat{BAC}=90^o\) (cmt) \(\Rightarrow AC\perp AB\Rightarrow AJ\perp AB\)
\(OD\perp AB\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường thẳng nối điểm đó với tâm đường tròn vuông góc với đường thẳng nối hai tiếp điểm) \(\Rightarrow OI\perp AB\)
=> AJ//OI (cùng vuông góc với AB) (2)
=> AIOJ là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
\(\widehat{BAC}=90^o\) (cmt)
=> AIOJ là hình chữ nhật (Hình bình hành có 1 góc trong bằng 90 độ là HCN)
b/
Ta có
IA=IB (Hai tiếp tuyến cùng xp từ 1 điểm thì đường thẳng nối điểm đó với tâm đường tròn vuông góc và chia đôi đường thẳng nối hai tiếp điểm)
JA=JC (Hai tiếp tuyến cùng xp từ 1 điểm thì đường thẳng nối điểm đó với tâm đường tròn vuông góc và chia đôi đường thẳng nối hai tiếp điểm)
=> IJ là đường trung bình của tg ABC => IJ//BC
c/
G là trọng tâm tg ABC \(\Rightarrow OG=\dfrac{1}{3}AO\) không đổi
=> Khi A di chuyển trên đường tròn thì G di chuyển trên đường tròn đường kính OG
\(\widehat{BAC}=90^o\)

\(2xy^2+2x+3y^2=4\left(x;y\inℤ\right)\)
\(\Leftrightarrow2x\left(y^2+1\right)+3y^2+3-3=4\)
\(\Leftrightarrow2x\left(y^2+1\right)+3\left(y^2+1\right)=7\)
\(\Leftrightarrow\left(2x+3\right)\left(y^2+1\right)=7\)
\(\Leftrightarrow\left(2x+3\right);\left(y^2+1\right)\in U\left(7\right)=\left\{-1;1-7;7\right\}\)
\(TH1:\left\{{}\begin{matrix}2x+3=-1\\y^2+1=-7\left(loại\right)\end{matrix}\right.\)
\(TH2:\left\{{}\begin{matrix}2x+3=1\\y^2+1=7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=-2\\y^2=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=\pm\sqrt[]{6}\left(loại\right)\end{matrix}\right.\)
\(TH3:\left\{{}\begin{matrix}2x+3=-7\\y^2+1=-1\left(loại\right)\end{matrix}\right.\)
\(TH1:\left\{{}\begin{matrix}2x+3=7\\y^2+1=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=4\\y^2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\) thỏa điều kiện đề bài
2xy² + 2x + 3y² = 4
2xy² + 2x + 3y² + 3 = 4 + 3
(2xy² + 2x) + (3y² + 3) = 7
2x(y² + 1) + 3(y² + 1) = 7
(y² + 1)(2x + 3) = 7
TH1: 2x + 3 = 1 và y² + 1 = 7
*) 2x + 3 = 1
2x = -2
x = -1 (nhận)
*) y² + 1 = 7
y² = 6
y = ±√6 (loại)
TH2: 2x + 3 = -1 và y² + 1 = -7
*) 2x + 3 = -1
2x = -4
x = -2 (nhận)
*) y² + 1 = -7
y² = -8 (vô lý)
TH3: 2x + 3 = 7 và y² + 1 = 1
*) 2x + 3 = 7
2x = 4
x = 2 (nhận)
*) y² + 1 = 1
y² = 0
y = 0 (nhận)
TH4: 2x + 3 = -7 và y² + 1 = -1
*) 2x + 3 = -7
2x = -10
x = -5 (nhận)
*) y² + 1 = -1
y² = -2 (vô lý)
Vậy ta được cặp giá trị (x; y) thỏa mãn: (2; 0)

\(P=\dfrac{x^4+5x^3-20x^2-27x+30}{x^2+4x-21}\left(1\right)\)
Điều kiện xác định khi và chỉ khi
\(x^2+4x-21\ne0\)
\(\Leftrightarrow x^2+7x-3x-21\ne0\)
\(\Leftrightarrow x\left(x+7\right)-3\left(x+7\right)\ne0\)
\(\Leftrightarrow\left(x-3\right)\left(x+7\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne3\\x\ne-7\end{matrix}\right.\)
Theo đề bài : \(\)
\(x=\sqrt[]{31-12\sqrt[]{3}}=\sqrt[]{27-12\sqrt[]{3}+4}=\sqrt[]{\left(3\sqrt[]{3}-2\right)^2}=\left|3\sqrt[]{3}-2\right|=3\sqrt[]{3}-2\)
\(\left(1\right)\Leftrightarrow P=\dfrac{x^4-3x^3+8x^3-24x^2+4x^2-12x-15x+45-15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{x^3\left(x-3\right)+8x^2\left(x-3\right)+4x\left(x-3\right)-15\left(x-3\right)-15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{\left(x-3\right)\left(x^3+8x^2+4x-15\right)-15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{x^3+8x^2+4x-15}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{x^3+7x^2+x^2+7x-3x-15}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{x^2\left(x+7\right)+x\left(x+7\right)-3\left(x+7\right)+6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{\left(x^2+x-3\right)\left(x+7\right)+6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=x^2+x-3+\dfrac{6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
Thay \(x=3\sqrt[]{3}-2\) vào \(P\) ta được
\(\Leftrightarrow P=\left(3\sqrt[]{3}-2\right)^2+3\sqrt[]{3}-2-3+\dfrac{6}{3\sqrt[]{3}-2+7}-\dfrac{15}{\left(3\sqrt[]{3}-2-3\right)\left(3\sqrt[]{3}-2+7\right)}\)
\(\Leftrightarrow P=31-12\sqrt[]{3}+3\sqrt[]{3}-5+\dfrac{6}{3\sqrt[]{3}+5}-\dfrac{15}{\left(3\sqrt[]{3}-5\right)\left(3\sqrt[]{3}+5\right)}\)
\(\Leftrightarrow P=26-9\sqrt[]{3}+\dfrac{6\left(3\sqrt[]{3}-5\right)}{\left(3\sqrt[]{3}+5\right)\left(3\sqrt[]{3}-5\right)}-\dfrac{15}{\left(3\sqrt[]{3}\right)^2-5^2}\)
\(\Leftrightarrow P=26-9\sqrt[]{3}+\dfrac{6\left(3\sqrt[]{3}-5\right)}{2}-\dfrac{15}{2}\)
\(\Leftrightarrow P=\dfrac{37}{2}-9\sqrt[]{3}+3\left(3\sqrt[]{3}-5\right)\)
\(\Leftrightarrow P=\dfrac{37}{2}-9\sqrt[]{3}+9\sqrt[]{3}-15\)
\(\Leftrightarrow P=\dfrac{37}{2}-15=\dfrac{7}{2}\)

Đkxđ: \(x\ge1\). Đặt \(\sqrt{x-1}=a\left(a\ge0\right)\) và \(\sqrt[3]{2-x}=b\left(b\le1\right)\)
Ta có \(\left\{{}\begin{matrix}a-b=5\\a^2+b^3=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=b+5\\\left(b+5\right)^2+b^3=1\end{matrix}\right.\)
\(\Rightarrow b^3+b^2+10b+24=0\)
\(\Leftrightarrow\left(b+2\right)\left(b^2-b+12\right)=0\)
\(\Leftrightarrow b=-2\) (do \(b^2-b+12>0\))
\(\Leftrightarrow\sqrt[3]{2-x}=-2\) \(\Leftrightarrow x=10\) (thỏa mãn)
Vậy pt đã cho có nghiệm duy nhất là \(x=10\)

Phương pháp:
Biểu thức √f(x)�(�) xác định ⇔f(x)≥0.⇔�(�)≥0.
Cách giải:
a) √x−3�−3
Biểu thức √x−3�−3 xác định ⇔x−3≥0⇔�−3≥0 ⇔x≥3.⇔�≥3.
Vậy x≥3�≥3 thì biểu thức √x−3�−3 xác định.
b) √−22x−1−22�−1
Biểu thức √−22x−1−22�−1 xác định ⇔−22x−1≥0⇔−22�−1≥0 ⇔2x−1<0⇔2�−1<0 ⇔x<12⇔�<12
Vậy với x<12�<12 thì biểu thức √−22x−1−22�−1 xác định.
a, \(\sqrt{x-3}\)
điều kiện để biểu thức xác định là:
\(x-3\) ≥ 0
\(x\ge\) 3
b, \(\sqrt{-2x^2-1}\)
Điều kiện để biểu thức trong căn xác định là:
- 2\(x^2\) - 1 ≥ 0
ta có \(x^2\) ≥ 0 ∀ \(x\)
⇒ -2\(x^2\) ≤ 0 ∀ \(x\) ⇒ -2\(x^2\) - 1 ≤ 0 ∀ \(x\)
Vậy không có giá trị nào của \(x\) để biểu thức trong căn có nghĩa hay
\(x\in\) \(\varnothing\)

1) đkxđ \(\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\y\ge0\end{matrix}\right.\)
Xét biểu thức \(P=x^3+y^3+7xy\left(x+y\right)\)
\(P=\left(x+y\right)^3+4xy\left(x+y\right)\)
\(P\ge4\sqrt{xy}\left(x+y\right)^2\)
Ta sẽ chứng minh \(4\sqrt{xy}\left(x+y\right)^2\ge8xy\sqrt{2\left(x^2+y^2\right)}\) (*)
Thật vậy, (*)
\(\Leftrightarrow\left(x+y\right)^2\ge2\sqrt{2xy\left(x^2+y^2\right)}\)
\(\Leftrightarrow\left(x+y\right)^4\ge8xy\left(x^2+y^2\right)\)
\(\Leftrightarrow x^4+y^4+6x^2y^2\ge4xy\left(x^2+y^2\right)\) (**)
Áp dụng BĐT Cô-si, ta được:
VT(**) \(=\left(x^2+y^2\right)^2+4x^2y^2\ge4xy\left(x^2+y^2\right)\)\(=\) VP(**)
Vậy (**) đúng \(\Rightarrowđpcm\). Do đó, để đẳng thức xảy ra thì \(x=y\).
Thế vào pt đầu tiên, ta được \(\sqrt{2x-3}-\sqrt{x}=2x-6\)
\(\Leftrightarrow\dfrac{x-3}{\sqrt{2x-3}+\sqrt{x}}=2\left(x-3\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}=2\end{matrix}\right.\)
Rõ ràng với \(x\ge\dfrac{3}{2}\) thì \(\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}\le\dfrac{1}{\sqrt{\dfrac{2.3}{2}-3}+\sqrt{\dfrac{3}{2}}}< 2\) nên ta chỉ xét TH \(x=3\Rightarrow y=3\) (nhận)
Vậy hệ pt đã cho có nghiệm duy nhất \(\left(x;y\right)=\left(3;3\right)\)

\(2.\left(a^2+15+b^2\right)\)
\(=2.\left(a^2.b^2.15\right)\)
\(=2a^2+2b^2+30\)

Đặt \(x^2+y^2=a\)
Khi đó ta được: \(P=\left(a+2\right)^3-\left(a-2\right)^3-12a^2\)
\(\Leftrightarrow P=a^3.6a^2+12a+8-a^3+6a^2-12a+8-12a^2\)
\(\Leftrightarrow P=\left(a^3-a^3\right)+\left(6a^2+6a^2-12a^2\right)+\left(12a-12a\right)+8+8\)
\(\Leftrightarrow P=16\)
Vậy \(P=16\) tại \(x=2019\) và \(y=2020\)
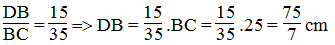
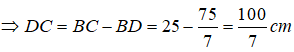
a) Ta chứng minh \(\Delta HAB~\Delta OMN\). Thật vậy, từ đề bài, dễ thấy H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác ABC. Vẽ đường tròn ngoại tiếp này. Dựng đường kính AD của (O). AH cắt BC tại E.
Ta thấy \(\widehat{ACD}=\widehat{AEB}\left(=90^o\right)\) và \(\widehat{ADC}=\widehat{ABE}\) (góc nội tiếp cùng chắn \(\stackrel\frown{AC}\)). \(\Rightarrow\Delta ACD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\widehat{BAH}=\widehat{CAO}\)
Mà \(\widehat{CAO}=\widehat{OCA}\), thêm vào đó tứ giác OMCN nội tiếp (vì \(\widehat{OMC}=\widehat{ONC}=90^o\)) nên \(\widehat{OMN}=\widehat{OCN}\). Do đó \(\widehat{HAB}=\widehat{OMN}\)
Hoàn toàn tương tự, ta suy ra \(\widehat{HBA}=\widehat{ONM}\). Từ đó suy ra \(\Delta HAB~\Delta OMN\left(g.g\right)\) (đpcm)
b) Ta thấy BH//CD\(\left(\perp AC\right)\) và CH//BD\(\left(\perp AB\right)\) nên tứ giác BDCH là hình bình hành. Mà M là trung điểm BC nên M cũng là trung điểm của DH. Lại có O là trung điểm của AD nên OM là đường trung bình của tam giác DHA \(\Rightarrow\left\{{}\begin{matrix}OM//AH\\OM=\dfrac{1}{2}AH\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\widehat{HAG}=\widehat{GMO}\\\dfrac{AH}{OM}=\dfrac{GA}{GM}\left(=2\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AHG~\Delta MOG\left(c.g.c\right)\) (đpcm)
c) Từ \(\Delta AHG~\Delta MOG\Rightarrow\widehat{AGH}=\widehat{MGO}\)
Do A, G, M thẳng hàng nên \(\widehat{AGH}+\widehat{HGM}=180^o\)
Từ đó suy ra \(\widehat{HGM}+\widehat{MGO}=180^o\) \(\Rightarrow\) H, O, G thẳng hàng.