Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAIB vuông tại I và ΔAIC vuông tại I có
AB=AC
AI chung
Do đó: ΔAIB=ΔAIC
b: ΔAIB=ΔAIC
=>IB=IC
=>I là trung điểm của BC
ΔAIB=ΔAIC
=>\(\widehat{IAB}=\widehat{IAC}\)
=>AI là phân giác của góc BAC
c: E là trung điểm của BI
=>\(BE=EI=\dfrac{BI}{2}=\dfrac{CI}{2}\)
=>\(\dfrac{CI}{CE}=\dfrac{2}{3}\)
Xét ΔCAK có
CE là đường trung tuyến
\(CI=\dfrac{2}{3}CE\)
Do đó: I là trọng tâm của ΔCAK
Xét ΔCAK có
I là trọng tâm
F là trung điểm của AC
Do đó: K,I,F thẳng hàng

\(\left(x-1\right)\left(2x+2\right)-\left(x-1\right)\left(x-2\right)-\left(x+3\right)\left(x+4\right)=0\)
=>\(2x^2+2x-2x-2-\left(x^2-3x+2\right)-\left(x^2+7x+12\right)=0\)
=>\(2x^2-2-x^2+3x-2-x^2-7x-12=0\)
=>-4x-14=0
=>4x=-14
=>\(x=-\dfrac{7}{2}\)
(\(x\) - 1)(2\(x\) + 2) - (\(x-1\))(\(x-2\)) - (\(x\) + 3)(\(x\) + 4) = 0
(\(x-1\))(2\(x\) + 2 - \(x\) + 2) - (\(x+3\))(\(x\) + 4) = 0
(\(x-1\))(\(x\) + 4) - (\(x\) + 3)(\(x\) + 4) = 0
(\(x\) + 4)(\(x-1-x-3\)) = 0
(\(x+4\)).(-4) = 0
\(x\) + 4 = 0
\(x\) = - 4
Vậy \(x\) = - 4

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
c: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
d: Xét ΔMHK có MH=MK
nên ΔMHK cân tại M

\(N=\dfrac{2}{2^1}+\dfrac{3}{2^2}+\dfrac{4}{2^3}+...+\dfrac{2019}{2^{2018}}\)
\(\Rightarrow2N=\dfrac{2}{1}+\dfrac{3}{2^1}+\dfrac{4}{2^2}+...+\dfrac{2019}{2^{2017}}\)
\(\Rightarrow2N-N=2+\dfrac{1}{2^1}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2017}}-\dfrac{2019}{2^{2018}}\)
\(\Rightarrow N=2+\dfrac{1}{2^1}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2017}}-\dfrac{2019}{2^{2018}}\)
\(\Rightarrow2N=4+1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{1016}}-\dfrac{2019}{2^{2017}}\)
\(\Rightarrow2N-N=3-\dfrac{2020}{2^{2017}}+\dfrac{2019}{2^{2018}}\)
\(\Rightarrow N=3-\dfrac{1}{2^{2018}}\left(2.2020-2019\right)=3-\dfrac{2021}{2^{2018}}\)
Do \(0< \dfrac{2021}{2^{2018}}< 1\Rightarrow2< N< 3\)
\(\Rightarrow N\) nằm giữa 2 số tự nhiên liên tiếp nên N ko là số tự nhiên

a: \(A⋮B\)
=>\(x^3+3x^2+5x+a⋮x+3\)
=>\(x^3+3x^2+5x+15+a-15⋮x+3\)
=>a-15=0
=>a=15
b: \(M⋮N\)
=>\(x^3-3x+a⋮x^2-2x+1\)
=>\(x^3-2x^2+x+2x^2-4x+2+a-2⋮x^2-2x+1\)
=>a-2=0
=>a=2

Bài 1b;
\(x^2\) - a\(x\) + 3 ⋮ \(x\) - 3
Theo bezout ta có: \(x^2\) - a\(x\) + 3 ⋮ \(x\) - 3
⇔32 - a.3 + 3 = 0
\ 9 - 3a + 3 = 0
12 - 3a = 0
3a = 12
a = 12 : 3
a = 4
Vậy \(x^2\) - a\(x\) + 3 \(⋮\) \(x\) - 3 khi a = 4

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔABC cân tại A có \(\widehat{ABC}=60^0\)
nên ΔABC đều
=>\(\widehat{BAC}=60^0\)
c: Xét ΔABC có
AH,BE là các đường cao
AH cắt BE tại I
Do đó: I là trực tâm của ΔABC
=>CI\(\perp\)AB tại K

\(P=\dfrac{100^{2024}+9}{100^{2024}-11}=\dfrac{100^{2024}-11+20}{100^{2024}-11}=1+\dfrac{20}{100^{2024}-11}\)
\(Q=\dfrac{100^{2023}+8}{100^{2023}-12}=\dfrac{100^{2023}-12+20}{100^{2023}-12}=1+\dfrac{20}{100^{2023}-12}\)
\(100^{2024}>100^{2023};-11>-12\)
Do đó: \(100^{2024}-11>100^{2023}-12\)
=>\(\dfrac{20}{100^{2024}-11}< \dfrac{20}{100^{2023}-12}\)
=>\(\dfrac{20}{10^{2024}-11}+1< \dfrac{20}{100^{2023}-12}+1\)
=>P<Q
Ta có P=\(\dfrac{100^{2024}+9}{100^{2024}-11}\)=\(\dfrac{9}{-11}\)=\(\dfrac{-9}{11}\)
Q=\(\dfrac{100^{2023}+8}{100^{2023}-12}\)=\(\dfrac{8}{-12}\)=\(\dfrac{-8}{12}\)
Do \(\dfrac{-8}{12}\)>\(\dfrac{-9}{11}\)⇒Q>P
tick nha

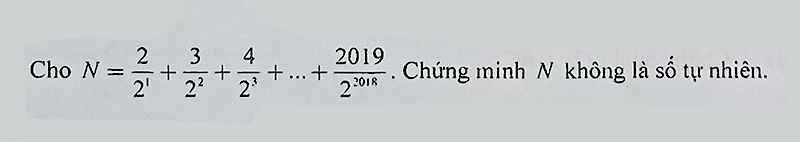

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>BA=BE và DA=DE
Xét ΔDAM vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADM}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAM=ΔDEC
=>DM=DC và AM=EC
Ta có: DM=DC
=>D nằm trên đường trung trực của MC(1)
Ta có: BA+AM=BM
BE+EC=BC
mà BA=BE và AM=EC
nên BM=BC
=>B nằm trên đường trung trực của MC(2)
Từ (1),(2) suy ra BD là đường trung trực của MC