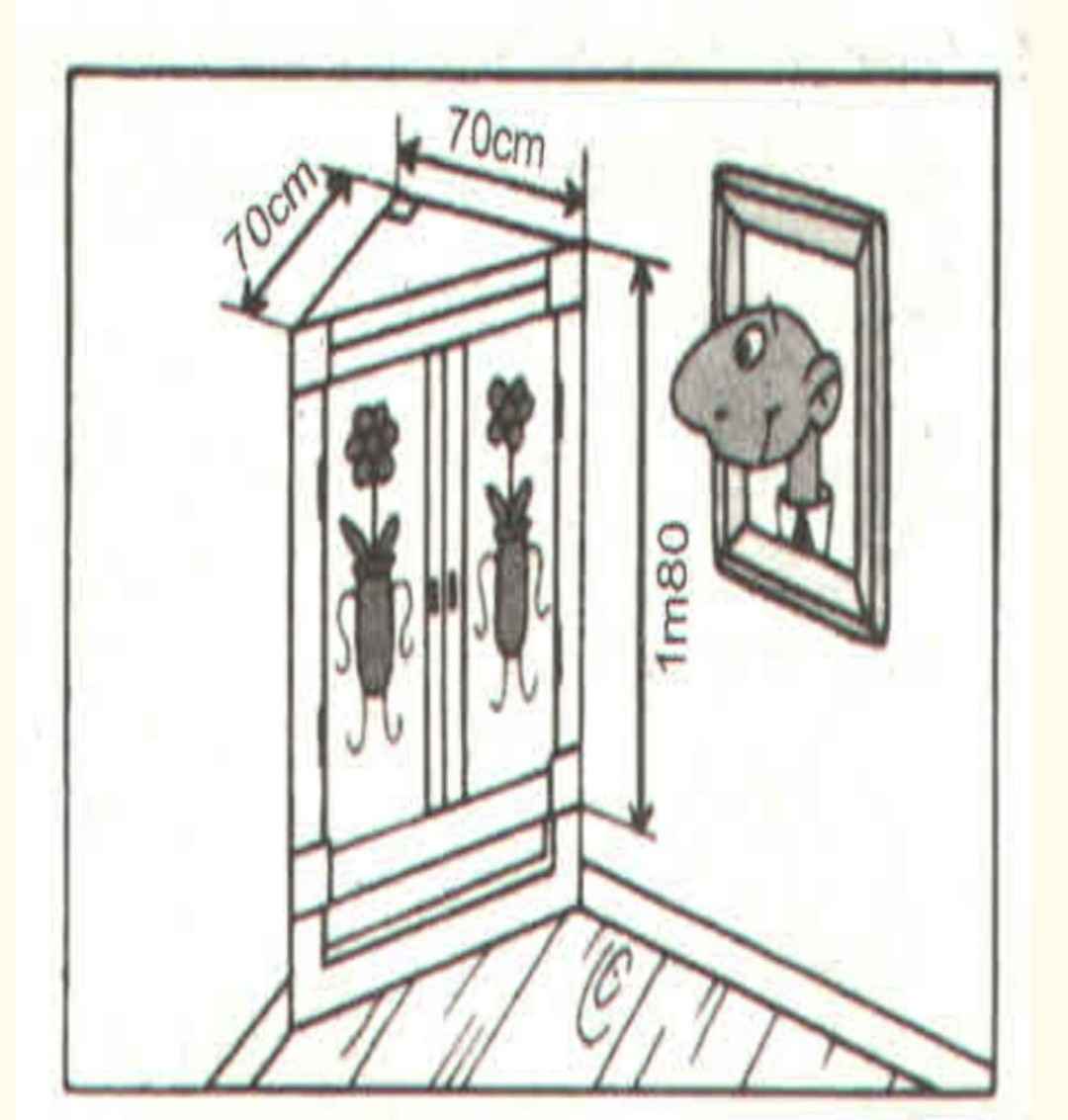
Diện tích của cái tủ hình lăng trụ đứng có các kích thước như trong hình vẽ sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2)
\(a,8,2\times3,5+115+3,5\times1,8\\ =\left(8,2\times3,5+3,5\times1,8\right)+115\\ =3,5\times\left(8,2+1,8\right)+115\\ =3,5\times10+115\\ =35+115\\ =150\\ b,0,125\times0,12\times25\times1,7\times8\\ =\left(0,125\times8\right)\times\left(0,12\times25\right)\times1,7\\ =1\times3\times1,7\\ =3\times1,7\\ =5,1\)
Bài 1:
a: \(\left(57,17+8,63\right)\times9,5-98,44:2,3\)
=65,8x9,5-42,8
=625,1-42,8=582,3
b: \(61,35-8,6\times7,2:4,8+52,45\)
=61,35+52,45-12,9
=113,8-12,9=100,9

\(P=\dfrac{-\left(x^2+1\right)+2x^2-8x+8}{x^2+1}=-1+\dfrac{2\left(x-2\right)^2}{x^2+1}\ge-1\)
\(P_{min}=-1\) khi \(x-2=0\Rightarrow x=2\)
\(P=\dfrac{9\left(x^2+1\right)-8x^2-8x-2}{x^2+1}=9-\dfrac{2\left(2x+1\right)^2}{x^2+1}\le9\)
\(P_{max}=9\) khi \(2x+1=0\Rightarrow x=-\dfrac{1}{2}\)
\[
P = \frac{x^2 - 8x + 7}{x^2 + 1}
\]
\[
x^2 - 8x + 7 = (x^2 - 8x + 16) - 9 = (x-4)^2 - 9
\]
\[
P = \frac{(x-4)^2 - 9}{x^2 + 1}
\]
- Tại \( x = 0 \):
\[
P(0) = \frac{0^2 - 8 \times 0 + 7}{0^2 + 1} = \frac{7}{1} = 7
\]
- Tại \( x = 1 \):
\[
P(1) = \frac{1^2 - 8 \times 1 + 7}{1^2 + 1} = \frac{1 - 8 + 7}{2} = \frac{0}{2} = 0
\]
- Tại \( x = 2 \):
\[
P(2) = \frac{2^2 - 8 \times 2 + 7}{2^2 + 1} = \frac{4 - 16 + 7}{4 + 1} = \frac{-5}{5} = -1
\]
- Tại \( x = 4 \)
\[
P(4) = \frac{4^2 - 8 \times 4 + 7}{4^2 + 1} = \frac{16 - 32 + 7}{16 + 1} = \frac{-9}{17}
\]
- Tại \( x = -1 \):
\[
P(-1) = \frac{(-1)^2 - 8 \times (-1) + 7}{(-1)^2 + 1} = \frac{1 + 8 + 7}{1 + 1} = \frac{16}{2} = 8
\]
Dựa trên các giá trị đã tính, ta thấy rằng giá trị lớn nhất của \( P \) là \( 8 \) và giá trị nhỏ nhất là \( -1 \).
=> Max = 8
Min = -1

\(E=x^2-2xy+3y^2-2x-10y+20\\
=\left(x^2+y^2+1-2xy-2x+2y\right)+\left(2y^2-12y+72\right)-53\\
=\left(-x+y+1\right)^2+2\left(y-6\right)^2-53\)
Ta có:
`(-x+y+1)^2>=0` với mọi x,y
`2(y-6)^2>=0` với mọi y
`=>E=(-x+y+1)^2+2(y-6)^2-53>=-53` với mọi x,y
Dấu "=" xảy ra: `-x+y+1=0` và `y-6=0`
`<=>-x+7=0` và `y=6`
`<=>x=7` và `y=6`

\(D=\left(x^2-2xy+y^2\right)-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y\right)^2-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y-6\right)^2+5y^2+9\)
Do \(\left\{{}\begin{matrix}\left(x-y-6\right)^2\ge0\\5y^2\ge0\end{matrix}\right.\) ;\(\forall x;y\)
\(\Rightarrow D\ge9\)
\(D_{min}=9\) khi \(\left\{{}\begin{matrix}x-y-6=0\\5y^2=0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(6;0\right)\)

Ta có:
`14a + 21b + 5a - 2b`
`= (14a + 5a)+(21b - 2b)`
`= 19a + 19b`
`= 19. (a + b)`
`= 19 . 100`
`= 1900`
Vậy: `14a + 21b + 5a - 2b = 1900` với `a+b=100`

a: Xét ΔAHD vuông tại H và ΔDCB vuông tại C có
\(\widehat{ADH}=\widehat{DBC}\)(hai góc so le trong, AD//BC)
Do đó: ΔAHD~ΔDCB
b: Xét ΔBHA vuông tại H và ΔBAD vuông tại A có
\(\widehat{HBA}\) chung
DO đó ΔBHA~ΔBAD
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BD}\)
=>\(BH\cdot BD=BA^2\)
c: ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(BH\cdot BD=BA^2\)
=>\(BH=\dfrac{3^2}{5}=1,8\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH=\sqrt{3^2-1,8^2}=2,4\left(cm\right)\)

\(1,M+N\\ =\left(2x^2-4xy+6y^2\right)+\left(2x^2+2xy-4y^2\right)\\ =2x^2-4xy+6y^2+2x^2+2xy-4y^2\\ =\left(2x^2+2x^2\right)+\left(-4xy+2xy\right)+\left(6y^2-4y^2\right)\\ =4x^2-2xy+2y^2\\ 2,M+\left(x^3-2xy^2+y^3\right)=x^3+5xy^2-y^3\\ =>M=\left(x^3+5xy^2-y^3\right)-\left(x^3-2xy^2+y^3\right)\\ =>M=x^3+5xy^2-y^3-x^3+2xy^2-y^3\\ =>M=\left(x^3-x^3\right)+\left(5xy^2+2xy^2\right)+\left(-y^3-y^3\right)\\ =>M=7xy^2-2y^3\)
1)
M + N = (2x² - 4xy + 6y²) + (2x² + 2xy - 4y²)
= 2x² - 4xy + 6y² + 2x² + 2xy - 4y²
= (2x² + 2x²) + (-4xy + 2xy) + (6y² - 4y²)
= 4x² - 2xy + 2y²
2)
M + (x³ - 2xy² + y³) = x³ + 5xy² - y³
M = x³ + 5xy² - y³ - (x³ - 2xy² + y³)
= x³ + 5xy² - y³ - x³ + 2xy² - y³
= (x³ - x³) + (5xy² + 2xy²) + (-y³ - y³)
= 7xy² - 2y³

\(a,2025-\left(2023-2022\right)^{2024}+\left(2024+1\right)^0\\ =2025-1^{2024}+2025^0\\ =2025-1+1\\ =2025\\ b,?\)
Nhìn đề câu b không hiểu bạn
`a, 2025 - (2023 - 2022)^2024+(2024+1)^0`
`= 2025 - 1^2024 + 2025^0`
`= 2025 - 1 +1`
`= 2024+1`
`=2025`
`b, (2^7)/13 . 3/(2^7)+ (2^10)/14 . 1/(2^6)`
`= 13/3+ (2^6 . 2^4)/14 . 1/(2^6)`
`= 13/3 + (2^4)/14`
`=13/3 + 16/14`
`= 115/21`

a, Diện tích xung quanh bể cá dạng hình hộp chữ nhật là:
\(2\cdot\left(4+5\right)\cdot10=180\left(cm^2\right)\)
Diện tích toàn phần bể cá dạng hình hộp chữ nhật là:
\(180+2\cdot4\cdot5=220\left(cm^2\right)\)
Thể tích bể cá dạng hình hộp chữ nhật là:
\(4\cdot5\cdot10=200\left(cm^3\right)\)
b, Diện tích xung quanh khi đổ nước vào bể cao 8 cm là:
\(2\cdot\left(4+5\right)\cdot8=144\left(cm^2\right)\)
Diện tích toàn phần khi đổ nước vào bể cao 8 cm là:
\(144+2\cdot4\cdot5=184\left(cm^2\right)\)
Thể tích khi đổ nước vào bể cao 8 cm là:
\(4\cdot5\cdot8=160\left(cm^3\right)\)
c, Thể tích phần không chứa nước là:
\(200-160=40\left(cm^2\right)\)
d, Tổng thể tích sau khi bỏ đá là:
\(160+100=260\left(cm^3\right)\)
Nước tràn ra ngoài là:
\(260-200=60\left(cm^3\right)\)
a) Diện tích xung quanh của bể cá là:
\(\left(4+5\right)\times2\times10=180\left(cm^2\right)\)
Diện tích toàn phần của bể cá là:
\(180+2\times4\times5=220\left(cm^2\right)\)
Thể tích của bể là:
\(4\times5\times10=200\left(cm^3\right)\)
b) Diện tích xung quanh:
\(\left(4+5\right)\times2\times8=144\left(cm^2\right)\)
Diện tích toàn phần:
\(144+2\times4\times5=184\left(cm^2\right)\)
Thể tích của nước có trong bể:
\(4\times5\times8=160\left(cm^3\right)\)
c) Diện tích phần không có nước là:
`200-160=40(cm^3)`
d) Khi bỏ cục đá vào thì thể tích của nước và cục đá là:
\(100+160=260\left(cm^2\right)\)
Vì: `260>200`
`=>` Nước bị tràn ra ngoài
Thể tích nước bị tràn là:
`260-200=60(cm^3)`
Độ dài cạnh đáy thứ ba của cái tủ là:
\(\sqrt{70^2+70^2}=70\sqrt{2}\left(cm\right)\)
Chu vi đáy của cái tủ là:
\(70+70+70\sqrt{2}=140+70\sqrt{2}\left(cm\right)\)
Diện tích xung quanh của của tủ là:
\(180\cdot\left(140+70\sqrt{2}\right)=25200+12600\sqrt{2}\left(cm^2\right)\)
Diện tích đáy của cái tủ là:
\(\dfrac{1}{2}\cdot70\cdot70=2450\left(cm^2\right)\)
Diện tích toàn phần của cái tủ là:
\(2\cdot2450+\left(25200+12600\sqrt{2}\right)=30100+12600\sqrt{2}\left(cm^2\right)\)