Xét ΔDMH vuông tại M và ΔDMC vuông tại M có

DM chung

MH=MC

Do đó: ΔDMH=ΔDMC

=>DH=DC và \(\widehat{DHC}=\widehat{DCH}\)

Ta có: \(\widehat{DHC}+\widehat{DHA}=90^0\)

\(\widehat{DCH}+\widehat{DAH}=90^0\)(ΔAHC vuông tại H)

mà \(\widehat{DHC}=\widehat{DCH}\)

nên \(\widehat{DHA}=\widehat{DAH}\)

=>DH=DA

mà DH=DC

nên DA=DC

=>D là trung điểm của AC

ΔABC cân tại A

mà AH là đường cao

nên H là trung điểm của BC

Xét ΔBAC có

H,D lần lượt là trung điểm của CB,CA

=>HD là đường trung bình của ΔBAC

=>HD//AB

Thì \(BA=BC\) và \(\widehat{A}=\widehat{C}\)

Trong một \(\Delta\)cân có:

 -) 2 cạch bên bằng nhau

-) 2 góc ở đáy bằng nhau

* Nếu trong một \(\Delta\)cân có một góc bằng \(60^o\) thì đó là \(\Delta\)đều.

Vậy cho tám giác ABC cân tại B thì:

\(AB=BC\)(2 cạch bên bằng nhau)

\(\widehat{A}=\widehat{C}\)(2 góc ở đáy bằng nhau)

Ta có: \(\Delta IEF=\Delta MNO\)

\(\Rightarrow\left\{{}\begin{matrix}EF=NO\text{ (hai cạnh tương ứng)}\\\widehat{IEF}=\widehat{MNO}\text{ (hai góc tương ứng)}\end{matrix}\right.\)

Thời gian 1 công nhân hoàn thành công việc đó là:

\(7\times12=84\) (giờ)

Nếu có 21 công nhân thì công việc đó sẽ hoàn thành trong:

\(84:21=4\) (giờ)

Giải: Ta thấy 

Số công nhân x thời gian = hằng số.

ban đầu: 12 công nhân x 7 giờ = 84 công nhân- giờ

Lúc sau số công nhân là 21 người, vậy thời gian hoàn thành công việc là:

T= 84/ 21 = 4 giờ

Đáp số: 4 giờ

a: Sửa đề: Phân giác của góc MAN cắt MN tại B

Xét ΔAMB vuông tại M và ΔACB vuông tại C có

AB chung

\(\widehat{MAB}=\widehat{CAB}\)

Do đó: ΔAMB=ΔACB

b: ΔAMB=ΔACB

=>AM=AC và BM=BC

Xét ΔBMG vuông tại M và ΔBCN vuông tại C có

BM=BC

\(\widehat{MBG}=\widehat{CBN}\)(hai góc đối đỉnh)

Do đó:ΔBMG=ΔBCN

=>BG=BN

=>B nằm trên đường trung trực của GN(1)

ΔBMG=ΔBCN

=>MG=CN

ta có: AM+MG=AG

AC+CN=AN

mà AM=AC và MG=CN

nên AG=AN

=>A nằm trên đường trung trực của GN(2)

Từ (1),(2) suy ra AB là đường trung trực của GN

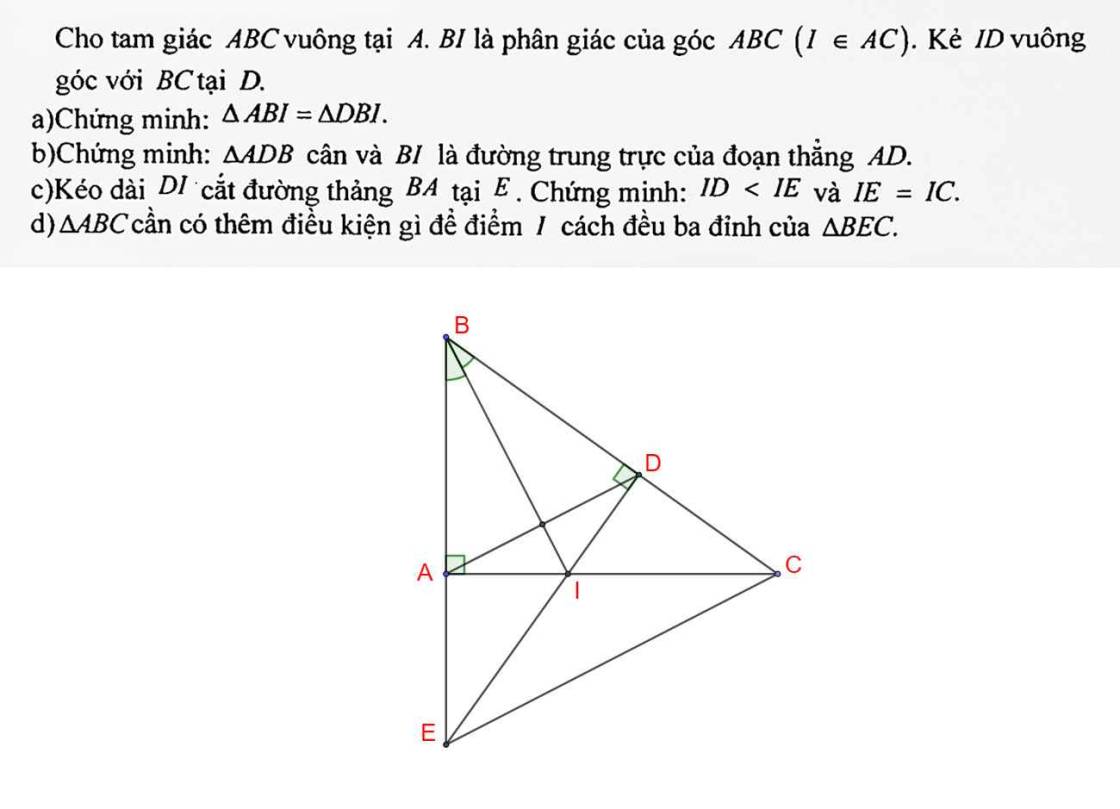
a) Do BI là tia phân giác của ∠ABC (gt)

⇒ ∠ABI = ∠CBI

⇒ ∠ABI = ∠DBI

Xét hai tam giác vuông: ∆ABI và ∆DBI có:

BI là cạnh chung

∠ABI = ∠DBI (cmt)

⇒ ∆ABI = ∆DBI (cạnh huyền - góc nhọn)

b) Do ∆ABI = ∆DBI (cmt)

⇒ AB = DB (hai cạnh tương ứng)

⇒ ∆ADB cân tại B

Do AB = DB (cmt)

⇒ B nằm trên đường trung trực của AD (1)

Do ∆ABI = ∆DBI (cmt)

⇒ IA = ID (hai cạnh tương ứng)

I nằm trên đường trung trực của AD (2)

Từ (1) và (2) ⇒ BI là đường trung trực của AD

c) ∆AIE vuông tại A

⇒ IE là cạnh huyền nên là cạnh lớn nhất

⇒ IA < IE

Mà IA = ID (cmt)

⇒ ID < IE

Xét hai tam giác vuông: ∆AIE và ∆DIC có:

IA = ID (cmt)

∠AIE = ∠DIC (đối đỉnh)

⇒ ∆AIE = ∆DIC (cạnh góc vuông - góc nhọn kề)

⇒ IE = IC (hai cạnh tương ứng)

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có

BC chung

\(\widehat{EBC}=\widehat{DCB}\)(ΔABC cân tại A)

Do đó: ΔEBC=ΔDCB

b: ΔEBC=ΔDCB

=>\(\widehat{ECB}=\widehat{DBC}\)

=>\(\widehat{HBC}=\widehat{HCB}\)

=>ΔHBC cân tại H

ta có: HB=HC

=>H nằm trên đường trung trực của BC(1)

ta có: AB=AC

=>A nằm trên đường trung trực của BC(2)

Từ (1),(2) suy ra AH là đường trung trực của BC

vẽ hình ra hộ cái

a: ΔABC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-52^0}{2}=\dfrac{128^0}{2}=64^0\)

Xét ΔABC có \(\widehat{ACB}>\widehat{BAC}\)

mà AB,BC lần lượt là cạnh đối diện của các góc ACB,BAC

nên AB>BC

b: Xét ΔAIB và ΔAIC có

AI chung

IB=IC

AB=AC

Do đó: ΔAIB=ΔAIC

a: Ta có: OA+AB=OB

OC+CD=OD

mà OA=OC và AB=CD

nên OB=OD

=>ΔOBD cân tại O

b: Xét ΔABD và ΔCDB có

AB=CD

\(\widehat{ABD}=\widehat{CDB}\)(ΔDOB cân tại O)

BD chung

Do đó: ΔABD=ΔCDB

=>\(\widehat{IDB}=\widehat{IBD}\)

=>ΔIBD cân tại I

=>IB=ID

Ta có: ΔABD=ΔCDB

=>AD=BC

ta có: AD=AI+ID

BC=BI+CI

mà ID=IB và AD=BC

nên IA=IC

=>ΔIAC cân tại I

c: Xét ΔOAI và ΔOCI có

OA=OC

AI=CI

OI chung

Do đó: ΔOAI=ΔOCI