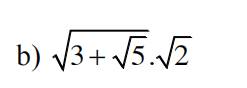
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


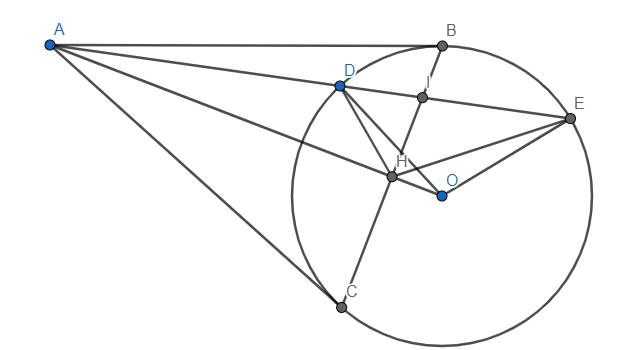
a) Do AB, AC tiếp xúc (O) tại B, C nên \(\widehat{OBA}=90^o\) và \(OA\perp BC\) tại H.
Xét tam giác OAB vuông tại B có đường cao BH, ta có \(OB^2=OA.OH\)
Mà \(OB=OD\left(=R_{\left(O\right)}\right)\) nên \(OD^2=OA.OH\). Từ đó suy ra \(\dfrac{OD}{OA}=\dfrac{OH}{OD}\). Từ đó dễ dàng suy ra 2 tam giác OHD và ODA đồng dạng.
b) Tam giác OAB vuông tại B có đường cao BH nên \(AB^2=AH.AO\)
Mặt khác, ta có \(\widehat{ABD}=\widehat{AEB}\) vì chúng lần lượt là góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung BD.
\(\Rightarrow\Delta ABD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)
Từ đó suy ra \(AH.AO=AD.AE\) hay \(\dfrac{AH}{AD}=\dfrac{AE}{AO}\). Do đó \(\Delta AHE~\Delta ADO\left(c.g.c\right)\) \(\Rightarrow\widehat{AEH}=\widehat{AOD}\) hay tứ giác OHDE nội tiếp.
\(\Rightarrow\widehat{AHD}=\widehat{DEO}=\widehat{ODE}=\widehat{OHE}\)
\(\Rightarrow90^o-\widehat{AHD}=90^o-\widehat{OHE}\) \(\Rightarrow\widehat{DHI}=\widehat{EHI}\).
Ta suy ra được đpcm.

\(\sqrt{\dfrac{11}{540}}\)
\(=\dfrac{\sqrt{11}}{\sqrt{540}}\)
\(=\dfrac{\sqrt{11}}{\sqrt{6^2\cdot15}}\)
\(=\dfrac{\sqrt{11}}{6\sqrt{15}}\)
\(=\dfrac{\sqrt{11}\cdot\sqrt{15}}{6\sqrt{15}\cdot\sqrt{15}}\)
\(=\dfrac{\sqrt{165}}{6\cdot15}\)
\(=\dfrac{\sqrt{165}}{90}\)

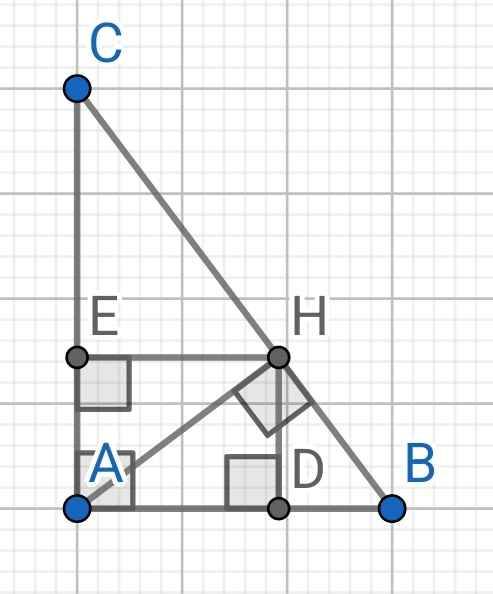 1) ∆ABC vuông tại A, AH là đường cao
1) ∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.CH = 4.9 = 36
⇒ AH = 6 (cm)
tanB = AH/BH = 6/4 = 3/2
⇒ ∠B ≈ 56⁰
2) a)
Do D, E lần lượt hình chiếu của H lên AB, AC
⇒ HD ⊥ AB và HE ⊥ AC
Tứ giác ADHE có:
∠HEA = ∠EAD = ∠ADH = 90⁰
⇒ ADHE là hình chữ nhật

DK: a≥0
Với dk ta có \(a+1\ge2\sqrt{a}\Leftrightarrow\dfrac{2\sqrt{a}}{a+1}\le1\)
Vậy GTLN của D là 1 khi a=1(Bất đẳng thức Cô si)

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

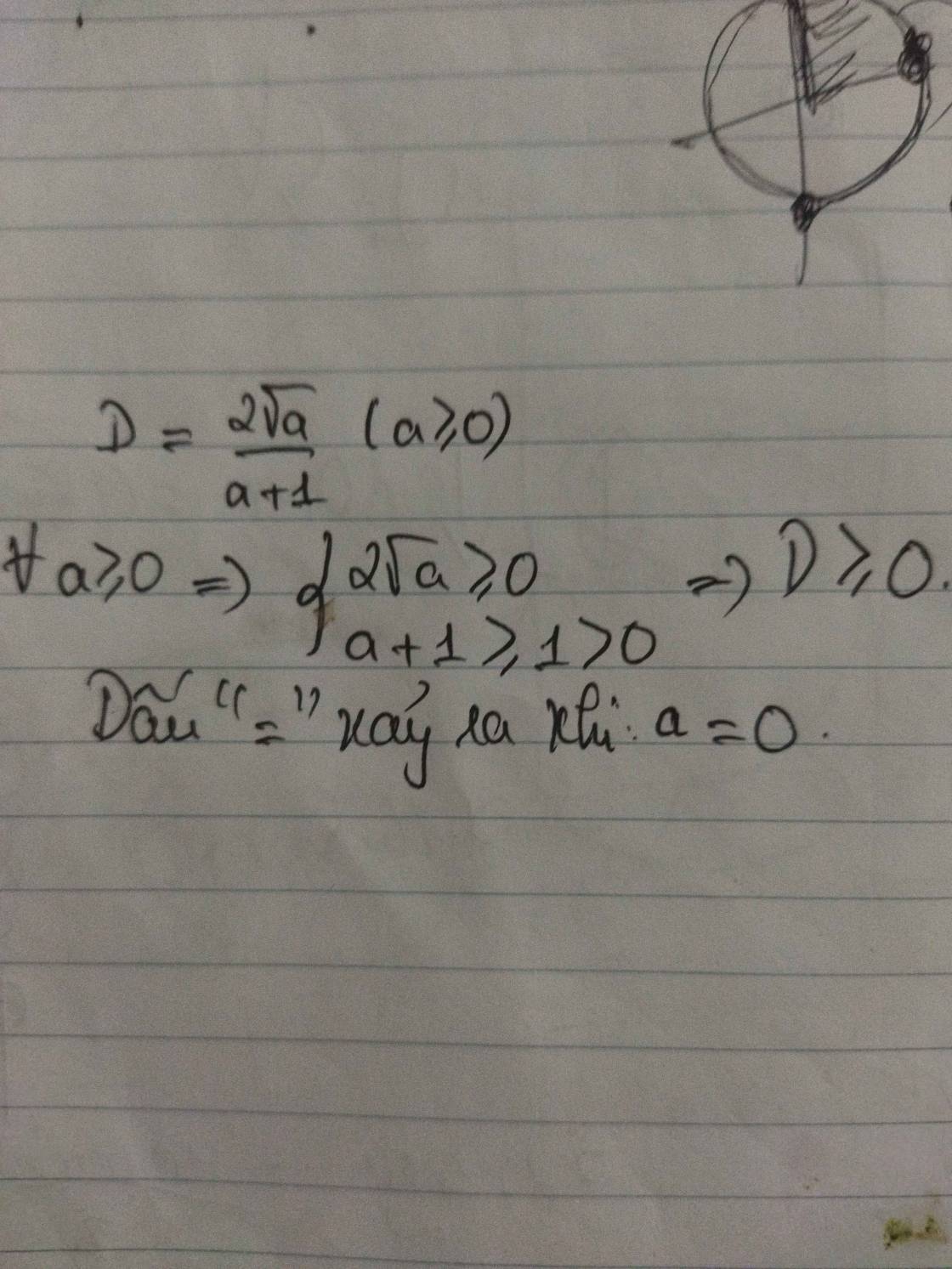

\(\sqrt{3+\sqrt{5}}\cdot\sqrt{2}\)
\(=\sqrt{2\cdot\left(3+\sqrt{5}\right)}\)
\(=\sqrt{6+2\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}\right)^2+2\cdot\sqrt{5}\cdot1+1^2}\)
\(=\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(=\left|\sqrt{5}+1\right|\)
\(=\sqrt{5}+1\)