Biểu thức đã cho lớn nhất khi x + √x + 1 nhỏ nhất

ĐKXĐ: x ≥ 0

⇒ x + √x + 1 ≥ 1

⇒ x + √x + 1 nhỏ nhất là 1 khi x = 0

Vậy giá trị lớn nhất của biểu thức đã cho là 5/1 = 5 khi x = 0

Biểu thức đã cho lớn nhất khi x + √x + 1 nhỏ nhất

ĐKXĐ: x ≥ 0

⇒ x + √x + 1 ≥ 1

⇒ x + √x + 1 nhỏ nhất là 1 khi x = 0

Vậy giá trị lớn nhất của biểu thức đã cho là 5/1 = 5 khi x = 0

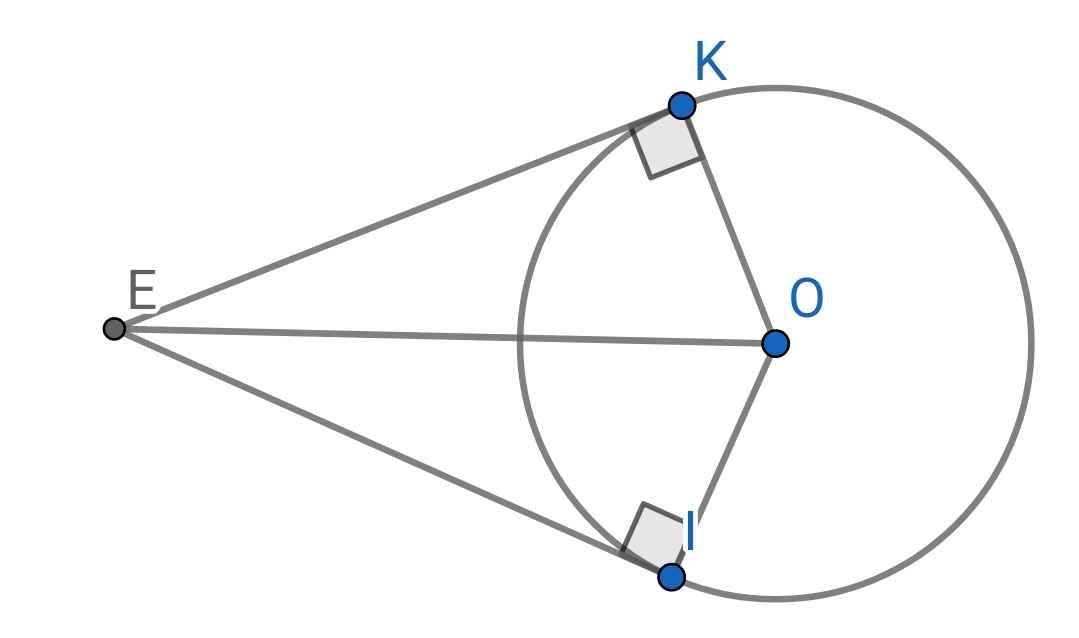  Do EI là tiếp tuyến của (O) tại I

⇒ EI OI

⇒ ∆OEI vuông tại I

⇒ O, E, I cùng thuộc đường tròn đường kính OE  (1)

Do EK là tiếp tuyến của (O) tại K

⇒ EK OK

⇒ ∆OEK vuông tại K

⇒ O, E, K cùng thuộc đường tròn đường kính OE  (2)

Từ (1) và (2) suy ra E, I, O, K cùng thuộc đường tròn đường kính OE

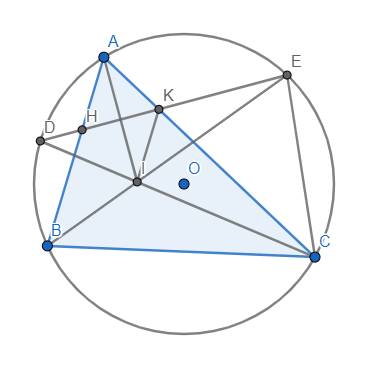
a) Ta có \(\widehat{AHK}=\dfrac{sđ\stackrel\frown{AE}+sđ\stackrel\frown{BD}}{2}\) 

và \(\widehat{AKH}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\)

 Mặt khác, do D, E lần lượt là điểm chính giữa của cung AB, AC nên \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{BD};sđ\stackrel\frown{AE}=sđ\stackrel\frown{CE}\). Từ đó \(\Rightarrow\widehat{AHK}=\widehat{AKH}\) hay tam giác AHK cân tại A (đpcm).

 b) Hiển nhiên I là tâm đường tròn nội tiếp tam giác ABC \(\Rightarrow\) AI là tia phân giác của \(\widehat{BAC}\) (hay chính là \(\widehat{HAK}\)). Mà theo câu a), tam giác AHK cân tại A nên AI đồng thời là đường cao của tam giác AHK \(\Rightarrow AI\perp HK\) hay \(AI\perp DE\) (đpcm)

 c) Ta có \(\widehat{CIE}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{BD}}{2}\)

\(=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\) \(=\widehat{CKE}\)  nên tứ giác CEKI nội tiếp 

 \(\Rightarrow\widehat{HKI}=\widehat{DCE}\) \(=\dfrac{sđ\stackrel\frown{DE}}{2}\) 

\(=\dfrac{sđ\stackrel\frown{DA}+sđ\stackrel\frown{AE}}{2}\)  \(=\dfrac{sđ\stackrel\frown{BD}+sđ\stackrel\frown{AE}}{2}\)  \(=\widehat{AHK}\)

Từ đó dễ dàng suy ra KI//AH hay KI//AB (đpcm)

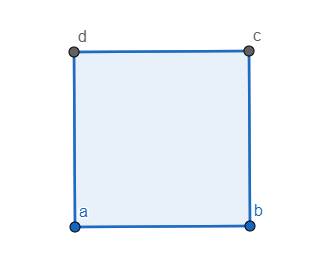
 Xét 1 mặt bất kì của khối lập phương như hình vẽ và gọi 4 số ở đỉnh là a, b, c, d. Khi đó do \(a+b+c,b+c+d,c+d+a,d+a+b\ge10\) nên \(3\left(a+b+c+d\right)\ge40\) \(\Rightarrow a+b+c+d\ge14\)

 Làm tương tự cho 4 mặt còn lại, ta đều được tổng của 4 số trên mỗi mặt đều không nhỏ hơn 14.

 Nhưng trong một mặt, sẽ có mặt có chứa đỉnh mang số 8. Khi đó 3 đỉnh còn lại bắt buộc là 1, 2, 3, mà \(1+2+3< 10\), vô lí. Lập luận tương tự cho trường hợp GTNN là 15, 16, 17. Nếu GTNN là 18, ta chỉ ra 1 trường hợp dấu "=" xảy ra:

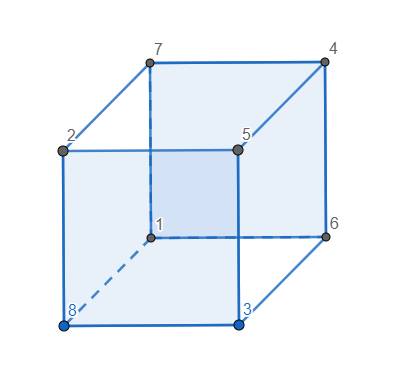
Vậy GTNN của 4 số trong cùng 1 mặt là 18.

Bạn tham khảo .

Xét 2 đường thẳng: \(y=\left(m^2+2\right)x+m\left(d\right)\)

                               \(y=6x+2\left(d'\right)\)

Để \(\left(d\right)//\left(d'\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2+2=6\\m\ne2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m\ne2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\ne2\end{matrix}\right.\)

\(\Leftrightarrow m=-2\)

Vậy.......

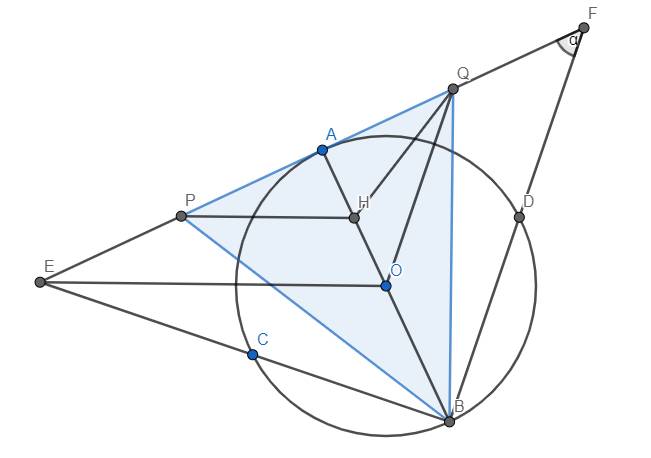
a) Định nghĩa lại H là trung điểm OA. Ta thấy OQ là đường trung bình của tam giác ABF nên OQ//BF. Hơn nữa \(BF\perp BE\) nên \(OQ\perp BE\). Lại có \(BA\perp QE\) nên O là trực tâm của tam giác BEQ \(\Rightarrow OE\perp BQ\)

 Mặt khác, PH là đường trung bình của tam giác AOE nên PH//OA. Do đó, \(PH\perp BQ\). Lại thấy rằng \(BH\perp PQ\) nên H là trực tâm tam giác BPQ (đpcm)

 b) Ta có \(P=\sin^6\alpha+\cos^6\alpha\) 

\(=\left(\sin^2\alpha\right)^3+\left(\cos^2\alpha\right)^3\)

\(=\left(\sin^2\alpha+\cos^2\alpha\right)\left(\sin^4\alpha+\cos^4\alpha-\sin^2\alpha\cos^2\alpha\right)\)

\(=1.\left[\left(\sin^2\alpha+\cos^2\alpha\right)^2-3\sin^2\alpha\cos^2\alpha\right]\)

\(=1-3\sin^2\alpha\cos^2\alpha\)

\(\le1-3.\dfrac{\left(\sin^2\alpha+\cos^2\alpha\right)^2}{4}\)

\(=\dfrac{1}{4}\)

 Dấu "=" xảy ra \(\Leftrightarrow\sin\alpha=\cos\alpha\) \(\Leftrightarrow\alpha=45^o\) hay 2 dây AB, CD vuông góc với nhau.

Vậy \(min_P=\dfrac{1}{4}\)

c) Ta có \(\left\{{}\begin{matrix}EC.EB=EA^2\\FD.FB=FA^2\end{matrix}\right.\)  (hệ thức lượng trong tam giác vuông)

\(\Rightarrow EC.EB.FD.FB=\left(EA.FA\right)^2\)

\(\Rightarrow EC.FD.\left(EB.DB\right)=AB^4\)

\(\Rightarrow EC.FD.\left(EF.AB\right)=AB^4\)

\(\Rightarrow EC.FD.EF=AB^3=CD^3\) (đpcm)

Ta có \(EC.DF=AC.AD=BC.BD\)

\(\Rightarrow\dfrac{EC}{DF}=\dfrac{BC.BD}{DF^2}\) 

\(=\dfrac{BC}{DF}.\dfrac{BD}{DF}\) 

\(=\dfrac{BE}{BF}.\dfrac{AC}{DF}\) 

\(=\dfrac{BE}{BF}.\dfrac{AE}{AF}\)

\(=\left(\dfrac{BE}{BF}\right)^3\)

Ta có đpcm.

Bài khá căng đấy

Lời giải:
Để $n^4+n^3+1$ là scp $\Leftrightarrow A=4n^4+4n^3+4$ cũng phải là scp

Xét $A-(2n^2+n+1)^2=4n^4+4n^3+4-(2n^2+n+1)^2=-5n^2-2n+3\leq -5-2n+3=-2-2n<0$ với mọi $n\geq 1$

$\Rightarrow A< (2n^2+n+1)^2(1)$

Xét $A-(2n^2+n-1)^2=4n^4+4n^3+4-(2n^2+n-1)^2=3n^2+2n+3>0$ với mọi $n\geq 1$

$\Rightarrow A> (2n^2+n-1)^2(2)$

Từ $(1); (2)\Rightarrow (2n^2+n-1)^2< A< (2n^2+n+1)^2$
$\Rightarrow A=(2n^2+n)^2$
$\Rightarrow (4n^4+4n^3+4)=(2n^2+n)^2$
$\Leftrightarrow 4-n^2=0$

$\Rightarrow n=2$

Lời giải:

$xy+yz+xz=1$
$\Rightarrow x^2+1=x^2+xy+yz+xz=(x+y)(x+z)$

Tương tự: $y^2+1=(y+z)(y+x); z^2+1=(z+x)(z+y)$

Khi đó:

\(\sum \sqrt{\frac{(x^2+1)(y^2+1)}{z^2+1}}=\sum \sqrt{\frac{(x+y)(x+z)(y+x)(y+z)}{(z+x)(z+y)}}=\sum \sqrt{(x+y)^2}\)

$=\sum (x+y)=2(x+y+z)$

Lời giải:

Áp dụng định lý Fermat nhỏ thì:

$2020^6\equiv 1\pmod 7$

$\Rightarrow (2020^6)^{336}.2020^4\equiv 1^{336}.2020^4\equiv 2020^4\pmod 7$

Có:

$2020\equiv 4\pmod 7$

$\Rightarrow 2020^4\equiv 4^4\equiv 256\equiv 4\pmod 7$

$\Rightarrow A\equiv 2020^4\equiv 4\pmod 7$

Vậy $A$ chia $7$ dư $4$