((2+x)/(2-x)+(4x^(2))/(4-x^(2))-(2-x)/(2+x))-:(x-1)/(2x-x^(2))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔCAB có AM là đường phân giác ngoài tại A
nên \(\dfrac{MB}{MC}=\dfrac{AB}{AC}\)
=>\(MB\cdot AC=AC\cdot AB\)
c: CB+BM=CM
=>CM=15+7=22(cm)
Xét ΔCMA có BN//MA
nên \(\dfrac{BN}{MA}=\dfrac{CB}{CM}\)
=>\(\dfrac{15}{22}=\dfrac{5}{AM}\)
=>\(AM=22\cdot\dfrac{5}{15}=\dfrac{22}{3}\left(cm\right)\)

Lời giải:
$\frac{x^2}{x^2+y^2}+\frac{z^2}{x^2+z^2}=\frac{2z}{y+z}$
$\Leftrightarrow \frac{x^4+2x^2z^2+y^2z^2}{(x^2+y^2)(x^2+z^2)}=\frac{2z}{y+z}$
$\Leftrightarrow (x^4+2x^2z^2+y^2z^2)(y+z)=2z(x^4+x^2z^2+x^2y^2+y^2z^2)$
$\Leftrightarrow x^4y-x^4z+2x^2yz^2-2x^2y^2z+y^3z^2-y^2z^3=0$
$\Leftrightarrow x^4(y-z)-2x^2yz(y-z)+y^2z^2(y-z)=0$
$\Leftrightarrow (y-z)(x^4-2x^2yz+y^2z^2)=0$
$\Leftrightarrow (y-z)(x^2-yz)^2=0$
$\Leftrightarrow y-z=0$ hoặc $x^2-yz=0$
$\Leftrightarrow y=z$ hoặc $x^2=yz$

Bài 12:
a: ĐKXĐ: \(x\notin\left\{3;2\right\}\)
b: Đặt \(A=\dfrac{x^2-4}{\left(x-3\right)\left(x-2\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x-3}\)
Thay x=13 vào A, ta được:
\(A=\dfrac{13+2}{13-3}=\dfrac{15}{10}=\dfrac{3}{2}\)
Bài 4:
1:
a: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{5x+10}{4x-8}\cdot\dfrac{4-2x}{x+2}\)
\(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}\)
\(=\dfrac{-10}{4}=-\dfrac{5}{2}\)
b: ĐKXĐ: \(x\notin\left\{-5;6\right\}\)
\(\dfrac{x^2-36}{2x+10}\cdot\dfrac{3}{6-x}\)
\(=\dfrac{\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)}\cdot\dfrac{-3}{x-6}\)
\(=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\)
2:
a: ĐKXĐ: x<>2
\(\dfrac{5x-10}{x^2+7}:\left(2x-4\right)\)
\(=\dfrac{5\left(x-2\right)}{x^2+7}:2\left(x-2\right)\)
\(=\dfrac{5\left(x-2\right)}{2\left(x-2\right)\left(x^2+7\right)}=\dfrac{5}{2\left(x^2+7\right)}\)
b: ĐKXĐ: \(x\notin\left\{-5;\dfrac{7}{3}\right\}\)
\(\left(x^2-25\right):\dfrac{2x+10}{3x-7}\)
\(=\left(x^2-25\right)\cdot\dfrac{3x-7}{2x+10}\)
\(=\left(x-5\right)\left(x+5\right)\cdot\dfrac{3x-7}{2\left(x+5\right)}\)
\(=\dfrac{\left(x-5\right)\left(3x-7\right)}{2}\)
c: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}\)
\(=\dfrac{x\left(x+1\right)}{5\left(x-1\right)^2}\cdot\dfrac{5\left(x-1\right)}{3\left(x+1\right)}\)
\(=\dfrac{x}{3\left(x-1\right)}\)

A) Số chấm chia hết cho 2 có thể là: 2; 4; 6 nên có 3 khả năng xảy ra
Gọi A là biến cố "mặt xuất hiện của xúc xắc có số chấm chia hết cho 2"
⇒ P(A) = 3/6 = 1/2
Các số chia hết cho 2 ở trong mặt xúc xắc là :2,4,6
Số % để gieo trúng các mặt đó là:
100 : 6 x 3 = 50%
Vậy 50 % là trúng các mặt đó.

a: ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=20^2\)
=>BC=20(cm)
Xét ΔBAC có BM là phân giác
nên \(\dfrac{AM}{AB}=\dfrac{CM}{CB}\)
=>\(\dfrac{AM}{12}=\dfrac{CM}{20}\)
=>\(\dfrac{AM}{3}=\dfrac{CM}{5}\)
mà AM+CM=AC=16cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{3}=\dfrac{CM}{5}=\dfrac{AM+CM}{3+5}=\dfrac{16}{8}=2\)
=>\(AM=2\cdot3=6\left(cm\right);CM=5\cdot2=10\left(cm\right)\)
Xét ΔABC có MN//BC
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AC}\)
=>\(\dfrac{MN}{20}=\dfrac{6}{16}=\dfrac{3}{8}\)
=>\(MN=20\cdot\dfrac{3}{8}=\dfrac{60}{8}=7,5\left(cm\right)\)
b: Bạn ghi lại đề nha bạn

Thay x=-5 và y=0 vào y=ax+b, ta được:
\(a\cdot\left(-5\right)+b=0\)
=>-5a+b=0(1)
Thay x=1 và y=3 vào y=ax+b, ta được:
\(a\cdot1+b=3\)
=>a+b=3(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-5a+b=0\\a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6a=-3\\a+b=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=3-\dfrac{1}{2}=\dfrac{5}{2}\end{matrix}\right.\)

$m - 3 = 2m + 5$
=> $m - 2m = 5 + 3$
=> $-m = 8$
=> $m = -8$

a; Hai đường thẳng đã cho song song với nhau khi và chỉ khi:
2m = m + 1
2m - m = 1
m = 1
Vậy với m = 1 thì hai đường thẳng đã cho song song với nhau
b; Hai đường thẳng đã cho cắt nhau khi và chi khi:
2m ≠ m + 1
2m - m ≠ 1
m ≠ 1
Vậy với m ≠ 1 thì hai đường thẳng đã cho cắt nhau
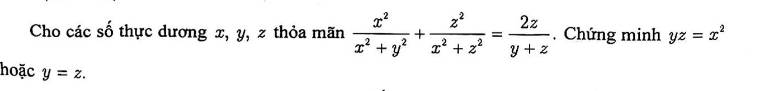 cho mình hởi bài này làm thế nào ạ
cho mình hởi bài này làm thế nào ạ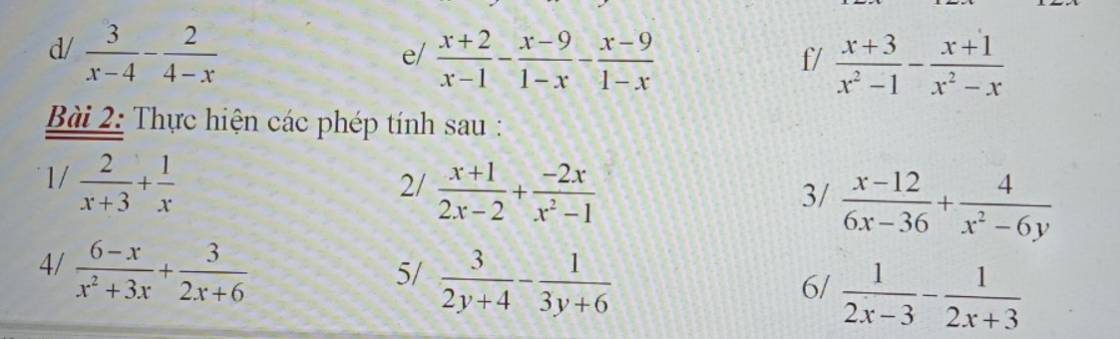

\(\left(\dfrac{2+x}{2-x}+\dfrac{4x^2}{4-x^2}\right)-\dfrac{2-x}{2+x}:\dfrac{-\left(x-1\right)}{2x-x^2}\)
\(=\left(\dfrac{-\left(x+2\right)}{x-2}-\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}\right)+\dfrac{x-2}{x+2}:\dfrac{-\left(x-1\right)}{-x\left(x-2\right)}\)
\(=\dfrac{-\left(x+2\right)^2-4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\cdot\dfrac{x\left(x-2\right)}{x-1}\)
\(=\dfrac{-5x^2-4x-4}{\left(x-2\right)\left(x+2\right)}+\dfrac{x\left(x-2\right)^2}{\left(x+2\right)\left(x-1\right)}\)
\(=\dfrac{\left(-5x^2-4x-4\right)\left(x-1\right)+x\left(x-2\right)^3}{\left(x-2\right)\left(x+2\right)\left(x-1\right)}\)
\(=\dfrac{-5x^3+5x^2-4x^2+4x-4x+4+x\left(x^3-6x^2+12x-8\right)}{\left(x-2\right)\left(x+2\right)\left(x-1\right)}\)
\(=\dfrac{-5x^3+x^2+4+x^4-6x^3+12x^2-8x}{\left(x-2\right)\left(x+2\right)\left(x-1\right)}\)
\(=\dfrac{x^4-11x^3+13x^2-8x+4}{\left(x-2\right)\left(x+2\right)\left(x-1\right)}\)