\(\dfrac{1}{99}-\dfrac{1}{99\cdot97}-\dfrac{1}{97\cdot95}-...-\dfrac{1}{3\cdot1}\)

\(=\dfrac{1}{99}-\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{97\cdot99}\right)\)

\(=\dfrac{1}{99}-\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)\)

\(=\dfrac{1}{99}-\dfrac{1}{2}\left(1-\dfrac{1}{99}\right)\)

\(=\dfrac{1}{99}-\dfrac{1}{2}\cdot\dfrac{98}{99}=\dfrac{1}{99}-\dfrac{49}{99}=-\dfrac{48}{99}=\dfrac{-16}{33}\)

Diện tích 1 viên gạch là: \(60\cdot60=3600\left(cm^2\right)=0,36\left(m^2\right)\)

Diện tích căn phòng là \(400\cdot0,36=144\left(m^2\right)\)

Độ dài cạnh của nền căn phòng là:

\(\sqrt{144}=12\left(m\right)\)

1553/990 nha!

Bước 1: Bật máy casio

Bước 2: nhập số 1,5

Bước 3: nhấn alpha

Bước 4: nhấn \(\sqrt{ }\) 

Bước 5: nhập chu kỳ vào trong dấu ngoặc

Bước 6: nhấn = khi đó ta được

1,5(68) = \(\dfrac{1553}{990}\)

Trên nửa mặt phẳng có bờ chứa tia Ox, có 2 tia oz và oy mà góc xOz < góc xOy ( 30độ < 110 độ) nên tia Oz nằm giữa 2 tia Ox và Oy

Ta có : xOz  +  zOy  =  xOy 

           30   +  zOy  =   110

                      zoy   = 110 - 30 = 80

ot là tia phân giác của zOy nen zot = toy =  80 : 2 = 40

xot = zot + xoz = 40 + 30 = 70

vậy 

      yOz = 80 độ

      zOt =  40 độ

      xOt =  70 độ

\(\dfrac{2^x}{16}=2\)

\(2^x:16=2\)

\(2^x=2\cdot16\)

\(2^x=32\)

\(2^x=2^5\)

\(x=5\)

Vậy...

2^x = 2.16

2^x = 32

2^x = 2⁵

=> x =5

Vậy x=5

Học tốt nhé e!!

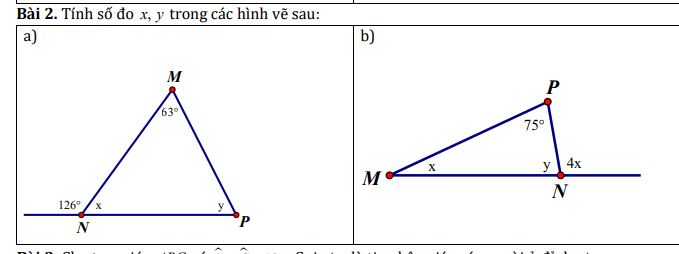
`a)`có : 

\(126^0+x=180^0\)(kề bù)

`=>`\(x=180^0-126^0=54^0\)

xét `ΔMNP` có :

\(\widehat{M}+\widehat{N}+\widehat{P}=180^0\)

`=>`\(\widehat{P}=x=180^0-63^0-54^0=63^0\)

`b)` gọi `Nz` là tia đối của `NM`

có : \(\widehat{PMz}\) là góc ngoài `ΔPNM`

`=>`\(4x=75^0+x\)

`=>`\(4x-x=75^0\)

`=>`\(3x=75^0\)

`=>x = 25^0`

Lại có : \(\widehat{PNM}+\widehat{PNz}=180^0\)(kề bù)

`=>`\(y+4\cdot25^0=180^0\)

`=> y+ 100^0 = 180^0`

`=> y = 180^0 - 100^0`

`=> y = 80^0`

Số nghịch đảo của `8/15` là `15/8`

Số nghịch đảo của `1/4` là `4`

         Kiến thức cần nhớ:

Chỉ có những phân số có tử, mẫu khác không mới có phân số nghịch đảo.

Muốn tìm phân số nghịch đảo ta chỉ cần đảo ngược tử số và phân số ban đầu. 

a: tia Oz nằm giữa hai tia Ox và Oy

=>\(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)

=>\(\widehat{xOz}=100^0-35^0=65^0\)

b: tia Oy nằm giữa hai tia Ox và Oz

=>\(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)

=>\(\widehat{xOz}=100^0+35^0=135^0\)

Ta có: \(\widehat{ADB}+\widehat{ADC}=180^o\) (2 góc kề bù)

Mà \(\widehat{ADC}=150^o\)

\(\Rightarrow\widehat{ADB}=30^o\)