Cho (o) đường kính BC ,lấy A thuốc (o) . Kẻ AH vuông góc với BC tại H , HÊ vuống góc với AB tại E , HF vuống góc với AV tại F . Gọi i là trung điểm của HC
a, Chứng minh tứ giác AEHF là hình chữ nhật
b, AE .AB = AF .AC
c, tính số đo góc BAC
d, C/m EF là tiếp tuyến của đường tròn ngoại tiếp tam giác HFC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



d3//d2 \(\Rightarrow a=-1\)
d3 cắt d1 tại điểm có hoành độ bằng 1
\(\Rightarrow a+b=2\)
Ta có hệ
\(\left\{{}\begin{matrix}a=-1\\a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\)

B= \(\dfrac{2023}{2-x}\) biểu thức B xác định ⇔ \(2-x\) \(\ne\) 0; \(x\ne\) 2
Kết luận biểu thức B xác định khi và chỉ khi \(x\) ≠ 2

Do A cách trục tung một khoảng bằng 7 nên x = 7
Thay x = 7 vào y = 3x - 2, ta có:
y = 3.7 - 2 = 19
Vậy A(7; 19)

Thay x = 1 vào (d₁), ta có:
y = 3.1 + 2 = 5
Thay x = 1; y = 5 vào (d₂), ta có:
-2.1 - m = 5
⇔ -2 - m = 5
⇔ m = -2 - 5
⇔ m = -7
Vậy m = -7 thì (d₁) và (d₂) cắt nhau tại điểm có hoành độ bằng 1

A B C O D E H K I M N P S
a/
Ta có
\(\widehat{ABO}=\widehat{ACO}=90^o\) => B và C cùng nhìn AO dưới 1 góc \(90^o\)
=> B; C nằm trên đường tròn đường kính AO => A; B; O; C cùng nằm trên 1 đường tròn
b/
Xét tg vuông ABO và tg vuông ACO có
OA chung; OB=OC (bán kính (O)) => tg ABO = tg ACO (hai tg vuông có cạnh huyền và cạnh góc vuông bằng nhau)
Xét tg ABH và tg ACH có
AH chung
AB=AC (2 tiếp tuyến cùng xp từ 1 điểm...)
tg ABO = tg ACO (cmt) \(\Rightarrow\widehat{BAO}=\widehat{CAO}\)
=> tg ABH = tg ACH (c.g.c) \(\Rightarrow\widehat{AHB}=\widehat{AHC}\) Mà \(\widehat{AHB}+\widehat{AHC}=\widehat{BHC}=180^o\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^o\Rightarrow OA\perp BC\) tại H
Ta có ID=IE (gt) \(\Rightarrow OI\perp DE\) (trong đường tròn đường thẳng đi qua tâm và trung điểm của dây cung thì vuông góc với dây cung)
Xét tg vuông AHK và tg vuông AIO có
\(\widehat{OAI}\) chung
=> tg AHK đồng dạng với tg AIO
\(\Rightarrow\dfrac{AH}{AI}=\dfrac{AK}{AO}\Rightarrow AH.AO=AK.AI\)
c/

A B H D C M O
a/
Ta có (M) tiếp xúc với AB tại H (gt) => AB là tiếp tuyến với (M)
Xét tg vuông ACM và tg vuông AHM có
AM chung
MC=MH (bán kính (M))
=> tg ACM = tg AHM (Hai tg vuông vó cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{AMC}=\widehat{AMH}\)
C/m tương tự khi xét 2 tg vuông BDM và BHM ta cũng có
\(\widehat{BMD}=\widehat{BMH}\)
Ta có
\(\widehat{AMH}+\widehat{BMH}=\widehat{AMB}=90^o\) (góc nt chắn nửa đường tròn)
\(\Rightarrow\widehat{AMC}+\widehat{BMD}=\widehat{AMH}+\widehat{BMH}=\widehat{AMB}=90^o\)
\(\Rightarrow\widehat{AMC}+\widehat{BMD}+\widehat{AMB}=90^o+90^o=180^o=\widehat{CMD}\)
=> C; M; D thẳng hàng
Ta có
\(AC\perp CD;BD\perp CD\) => AC//BD
b/ Ta có
AC//BD (cmt) => ACDB là hình thang
Mà
MC=MD (bán kính (M)
OA=OB=R
=> OM là đường trung bình của hình thang ACDB => OM//BD
Mà \(BD\perp CD\)
\(\Rightarrow OM\perp CD\) => CD là tiếp tuyến với (O)
c/
Ta có
AC=AH (2 tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn)
BD=BH (2 tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn)
\(\Rightarrow AC+BD=AH+BH=AB=2R\) không đổi
d/
Khi HC=HD => tg AHD cân tại H
Ta có MC=MD
\(\Rightarrow MH\perp CD\) (trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao)
Mà \(OM\perp CD\left(cmt\right)\)
\(\Rightarrow H\equiv O\)
Xét tg AMB có
\(MH\perp AB\Rightarrow MO\perp AB\)
Mà OA=OB
=> tg AMB cân tại M (tam giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
=> MA=MB => sđ cung MA = sđ cung MB (trong đường tròn 2 dây cung bằng nhau thì số đo 2 cung tương ứng bằng nhau)
=> M là điểm giưa cung AB

Lời giải:
a. $(d)$ cắt trục tung tại điểm có tung độ $3$, tức là cắt trục tung tại điểm $(0;3)$
$(0;3)\in (d)$
$\Leftrightarrow 3=(m+2).0+2m^2+1$
$\Leftrightarrow 2m^2=2$
$\Leftrightarrow m^2=1$
$\Leftrightarrow m=\pm 1$
Khi $m=1$ thì ta có hàm số $y=3x+3$
Khi $m=-1$ thì ta có hàm số $y=x+3$
Bạn có thể tự vẽ 2 đths này.
b.
Để $(d)$ cắt $(d')$ thì: $m+2\neq 2m+2$
$\Leftrightarrow m\neq 0$
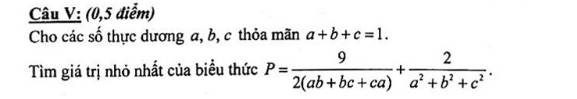 giúp e vs ạaa
giúp e vs ạaa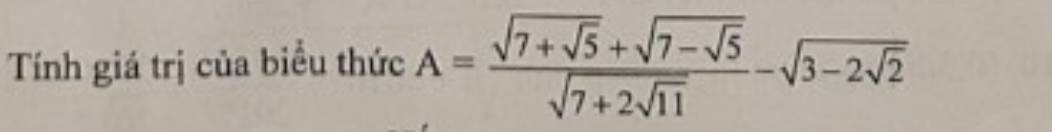
B C H A E F I
a/
Ta có
\(\widehat{BAC}=90^o\) (góc nt chắn nửa đường tròn)
\(\Rightarrow AB\perp AC\Rightarrow AE\perp AC;HF\perp AC\left(gt\right)\) => AE//HF
\(AC\perp AB\Rightarrow AF\perp AB;HE\perp AB\left(gt\right)\) => AF//HE
=> AEHF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{BAC}=90^o\left(cmt\right)\)
=> AEHF là hình CN
b/
Xét tg vuông EHA và tg vuông ABC có
\(\widehat{EAH}=\widehat{ACB}\) (cùng phụ với \(\widehat{ABC}\) )
=> tg EHA đồng dạng với tg ABC
\(\Rightarrow\dfrac{AE}{AC}=\dfrac{HE}{AB}\)
Mà AEHF là hình CN (cmt) => HE=AF (cạnh đối HCN)
\(\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\Rightarrow AE.AB=AF.AC\left(dpcm\right)\)
c/
\(\widehat{BAC}=90^o\left(cmt\right)\)
d/
Xét tg vuông HFC có
\(HI=CI\left(gt\right)\Rightarrow FI=HI=CI=\dfrac{HC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> H; F; C cùng nằm trên đường tròn đường kính HC tâm I
=> đường tròn tâm I đường kính HC là đường tròn ngoại tiếp tg HFC
=> tg IHF cân tại I \(\Rightarrow\widehat{IFH}=\widehat{IHF}\)
Ta có
HF//AB (cùng vuông góc với AC) \(\Rightarrow\widehat{IHF}=\widehat{ABC}\) (góc đồng vị)
\(\Rightarrow\widehat{IFH}=\widehat{ABC}\) (1)
Xét tg vuông EAH và tg vuông HFE có
HE chung; AE=HF (cạnh đối hình CN) => tg EAH = tg HFE (Hai tg vuông có 2 cạnh góc vuông bàng nhau)
\(\Rightarrow\widehat{EAH}=\widehat{HFE}\)
Mà \(\widehat{EAH}=\widehat{ACB}\left(cmt\right)\)
\(\Rightarrow\widehat{HFE}=\widehat{ACB}\) (2)
Mà \(\widehat{ABC}+\widehat{ACB}=90^o\) (3)
Từ (1) (2) (3)
\(\Rightarrow\widehat{IFH}+\widehat{HFE}=\widehat{IFE}=\widehat{ABC}+\widehat{ACB}=90^o\)
=> EF là tiếp tuyến với (I)