Giải phương trình: (6x+8)(6x+6)(6x+7)2 =72
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Để A là số nguyên thì \(n-5⋮n+1\)
=>\(n+1-6⋮n+1\)
=>\(-6⋮n+1\)
=>\(n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)
Khi n=0 thì \(A=\dfrac{0-5}{0+1}=-5< 0\)(nhận)
Khi n=-2 thì \(A=\dfrac{-2-5}{-2+1}=\dfrac{-7}{-1}=7>0\left(loại\right)\)
Khi n=1 thì \(A=\dfrac{1-5}{1+1}=\dfrac{-4}{2}=-2< 0\)(nhận)
Khi n=-3 thì \(A=\dfrac{-3-5}{-3+1}=\dfrac{-8}{-2}=4>0\)(loại)
Khi n=2 thì \(A=\dfrac{2-5}{2+1}=\dfrac{-3}{3}=-1< 0\)(nhận)
Khi n=-4 thì \(A=\dfrac{-4-5}{-4+1}=\dfrac{-9}{-3}=3>0\left(loại\right)\)
Khi n=5 thì \(A=\dfrac{5-5}{5+1}=0\left(loại\right)\)
Khi n=-7 thì \(A=\dfrac{-7-5}{-7+1}=\dfrac{-12}{-6}=2>0\left(loại\right)\)
b: \(A=\dfrac{n-5}{n+1}=\dfrac{n+1-6}{n+1}=1-\dfrac{6}{n+1}\)
Để A có giá trị nhỏ nhất thì \(-\dfrac{6}{n+1}\) nhỏ nhất
=>\(\dfrac{6}{n+1}\) lớn nhất
=>n+1=1
=>n=0
Để A có giá trị lớn nhất thì \(\dfrac{6}{n+1}\) nhỏ nhất
=>n+1=-1
=>n=-2

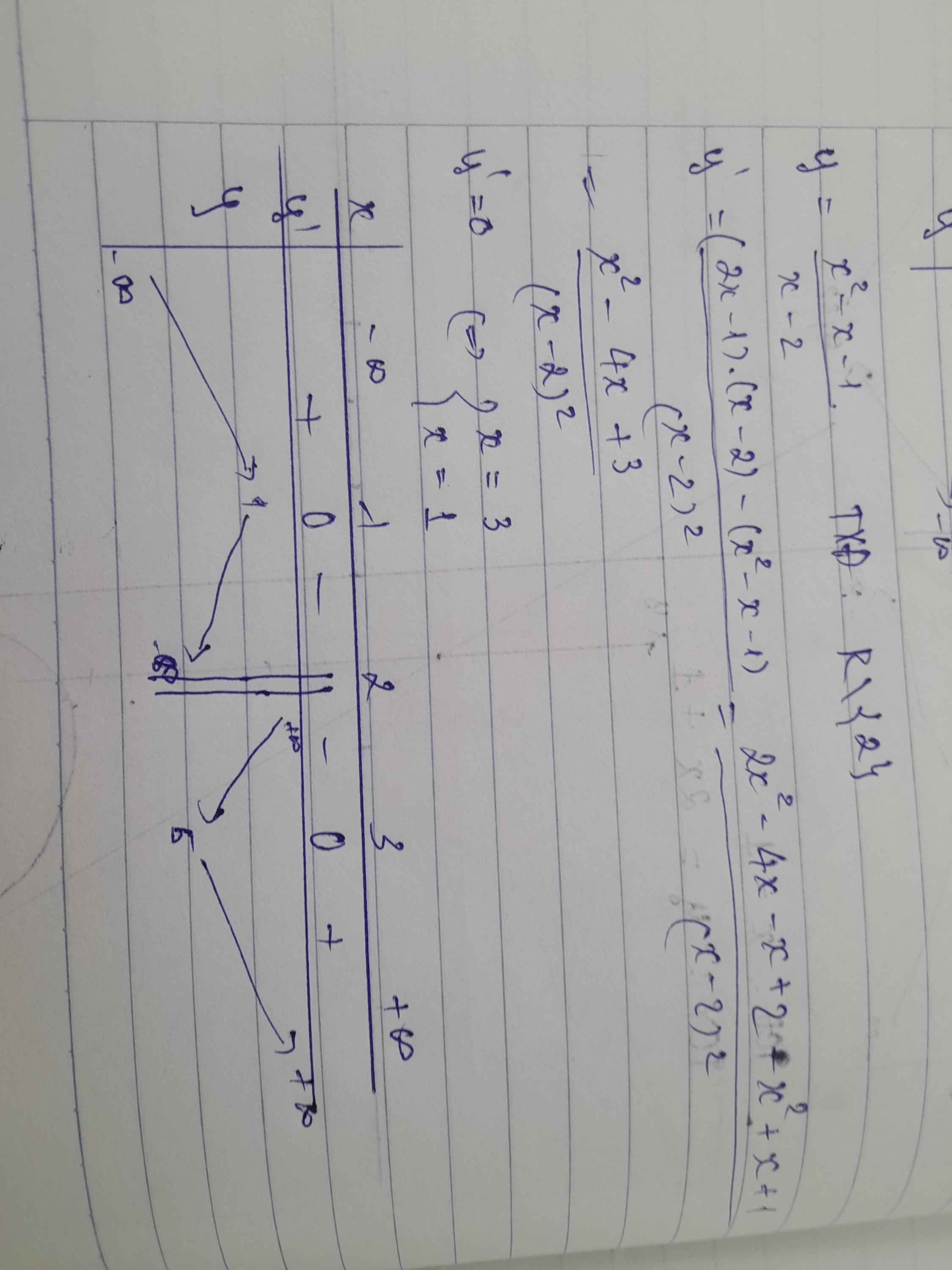
Tập xác định \(D=ℝ\backslash\left\{2\right\}\)
TCĐ: \(x=2\)
Có \(\dfrac{x^2-x-1}{x-2}=\dfrac{x^2-x-2+1}{x-2}=\dfrac{\left(x+1\right)\left(x-2\right)+1}{x-2}=\left(x+1\right)+\dfrac{1}{x-2}\)
nên đồ thị hàm số có tiệm cận xiên là đường \(y=x+1\)
Có \(y'=\dfrac{x^2-4x+3}{\left(x-2\right)^2}\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
BBT

1h15p=1,25(giờ)
Vận tốc lúc xuôi dòng là:
22,6+2,2=24,8(km/h)
Độ dài quãng sông AB là:
24,8x1,25=31(km)

136 nghìn đồng =100 000đ+30 000đ+6 000đ nên
số tiền 100 000đ cần trả là:100 000:100 000=1(tờ)
số tiền 10 000đ cần trả là:30 000:10 000=3(tờ)
số tiền 1 000đ cần trả là:6 000:1 000=6(tờ)
Vậy cần trả 1 tờ 100 000đ,3 tờ 10 000đ,6 tờ 1 000đ
TICK CHO MIK VỚI NHÉ

a) \(y=\dfrac{x+1}{x-2}\)
\(y'=-\dfrac{3}{\left(x-2\right)^2}< 0\forall x\inℝ\ \left\{2\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
b) \(y=\dfrac{2x+1}{x-1}\)
\(y'=-\dfrac{3}{\left(x-1\right)^2}< 0\forall x\inℝ\ \left\{1\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;1\right)\) và \((1;+\infty)\)


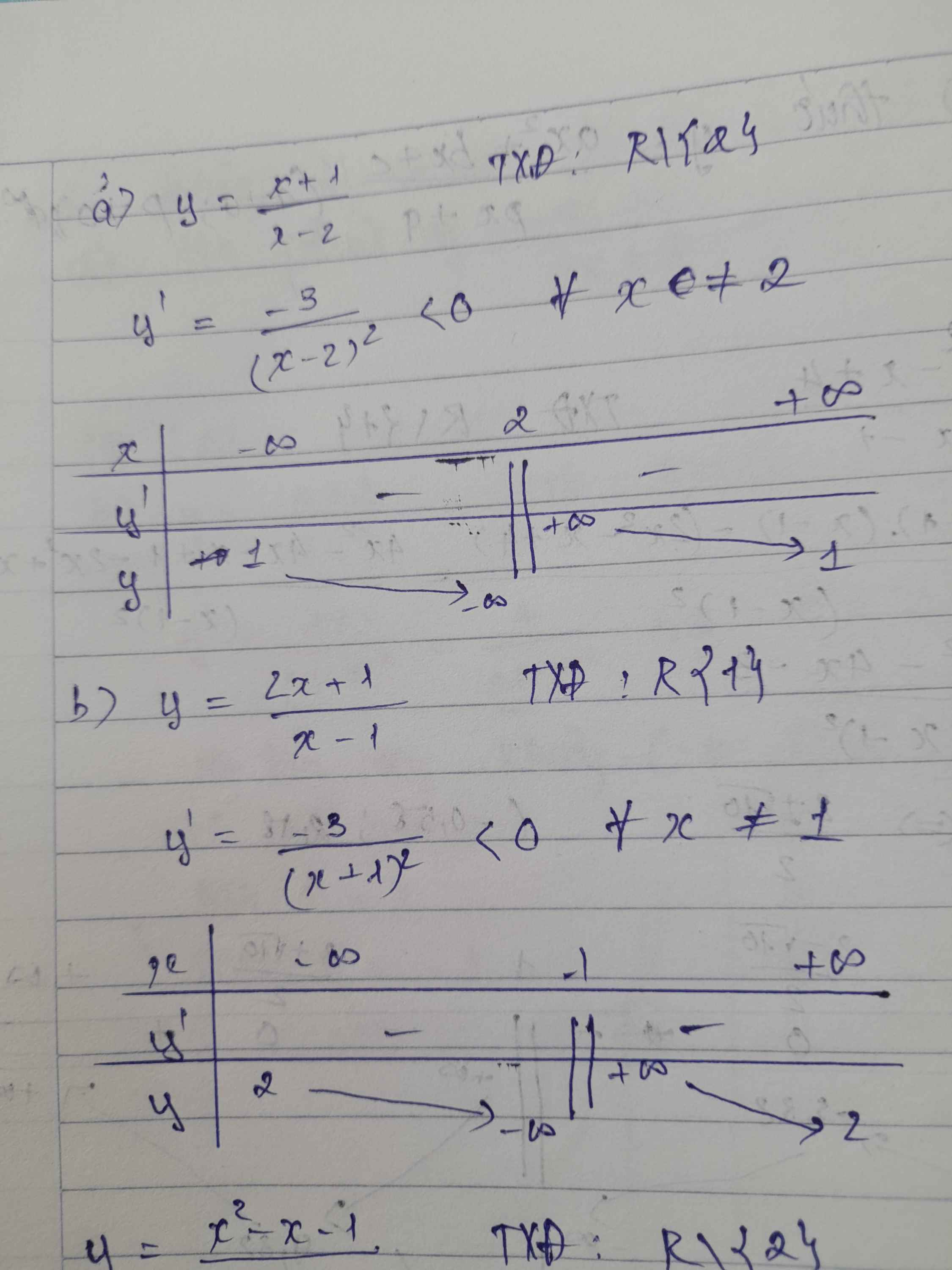


Đặt 6x+7=a
Phương trình sẽ trở thành \(\left(a+1\right)\left(a-1\right)\cdot a^2=72\)
=>\(a^2\left(a^2-1\right)=72\)
=>\(a^4-a^2-72=0\)
=>\(\left(a^2-9\right)\left(a^2+8\right)=0\)
mà \(a^2+8>0\forall a\)
nên \(a^2-9=0\)
=>(a-3)(a+3)=0
=>(6x+7-3)(6x+7+3)=0
=>(6x+4)(6x+10)=0
=>\(\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(\left(6x+8\right)\left(6x+6\right)\left(6x+7\right)^2=72\left(^∗\right)\)
Đặt: \(6x+7=t\)
\(\left(^∗\right)\Rightarrow\left(t+1\right)\left(t-1\right)t^2=72\\ \Leftrightarrow\left(t^2-1\right)t^2=72\\ \Leftrightarrow t^4-t^2-72=0\\ \Leftrightarrow\left(t^4-9t^2\right)+\left(8t^2-72\right)=0\\ \Leftrightarrow t^2\left(t^2-9\right)+8\left(t^2-9\right)=0\\ \Leftrightarrow\left(t^2+8\right)\left(t^2-9\right)=0\\ \Leftrightarrow\left(t^2+8\right)\left(t-3\right)\left(t+3\right)=0\\ \)
\(\Rightarrow\left[{}\begin{matrix}t^2+8=0\left(PTVN\right)\\t-3=0\\t+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=3\\t=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}6x+7=3\\6x+7=-3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
Vậy pt có tập nghiệm: \(S=\left\{-\dfrac{2}{3};-\dfrac{5}{3}\right\}\)