Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: VT=\(\left(a+1\right)\left(a^2-a+1\right)\)
\(=a^3-a^2+a+a^2-a+1\)
\(=a^3+1\)=VP
b: \(VT=\left(a+1\right)\left(a^3-a^2+a-1\right)\)
\(=a^4-a^3+a^2-a+a^3-a^2+a-1\)
\(=a^4-1=VP\)

\(f\left(x\right)⋮g\left(x\right)\)
=>\(2x^2-x+2⋮2x+1\)
=>\(2x^2+x-2x-1+3⋮2x+1\)
=>\(3⋮2x+1\)
=>\(2x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-1;1;-2\right\}\)

1: \(\left(x-\dfrac{1}{2}\right)^2>=0\forall x\)
=>\(A=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
2: \(\left|3x-1\right|>=0\forall x\)
=>\(\left|3x-1\right|-5>=-5\forall x\)
Dấu '=' xảy ra khi 3x-1=0
=>3x=1
=>\(x=\dfrac{1}{3}\)
3: \(\left(2-x\right)^2>=0\forall x\)
=>\(-\left(2-x\right)^2< =0\forall x\)
=>\(C=-\left(2-x\right)^2+5< =5\forall x\)
Dấu '=' xảy ra khi 2-x=0
=>x=2
4: \(\left(x^2-4\right)^2>=0\forall x\)
\(\left|y-x\right|>=0\forall x,y\)
Do đó: \(\left(x^2-4\right)^2+\left|y-x\right|>=0\forall x,y\)
=>\(D=\left(x^2-4\right)^2+\left|y-x\right|+3>=3\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x^2-4=0\\y-x=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{2;-2\right\}\\y=x\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}y=x=2\\y=x=-2\end{matrix}\right.\)
5: \(\left(x-1\right)^2>=0\forall x\)
\(\left(x^2-1\right)^4>=0\forall x\)
Do đó: \(E=\left(x-1\right)^2+\left(x^2-1\right)^4>=0\forall x\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-1=0\\x^2-1=0\end{matrix}\right.\)
=>x=1
6: \(\left(x+3\right)^2+3>=3\forall x\)
=>\(F=\dfrac{2}{\left(x+3\right)^2+3}< =\dfrac{2}{3}\forall x\)
Dấu '=' xảy ra khi x+3=0
=>x=-3
7: \(\left(x^2+1\right)^2>=1^2=1\forall x\)
=>\(\left(x^2+1\right)^2+2022>=2023\forall x\)
=>\(G=\dfrac{2023}{\left(x^2+1\right)^2+2022}< =\dfrac{2023}{2023}=1\forall x\)
Dấu '=' xảy ra khi x=0

Còn phụ thuộc vào nhiều yếu tố phụ kèm theo nữa em nhé.
+ Hạnh kiểm tốt
+ Không có môn nào dưới 6,5
....

Lời giải:
$P(1)=1^{2024}+1^{2023}+....+1+1P(1)$
$=\underbrace{1+1+...+1}_{2024}+P(1)=2024+P(1)$
$\Rightarrow 2024=0$ (vô lý)
Vậy không tồn tại $P(x)$ thỏa mãn đề.

\(-6x^8:\left(\dfrac{3}{7}x^4\right)=\left(-6:\dfrac{3}{7}\right)\cdot\left(x^8:x^4\right)=-14x^4\)
- 6\(x^8\) : (\(\dfrac{3}{7}\)\(x^4\))
= - 6\(x^8\) x \(\dfrac{7}{3x^4}\)
= - 14\(x^4\)

|x|=2
=>\(\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Thay x=2 vào D, ta được:
\(D=4\cdot2^3-8\cdot2+7=32-16+7=23\)
Thay x=-2 vào D, ta được:
\(D=4\cdot\left(-2\right)^3-8\cdot\left(-2\right)+7=-32+16+7=-16+7=-9\)

Theo bezout ta có:
F(\(x\)) = (5\(x^3\) + 4\(x^2\) - 6\(x\) - a) ⋮ (5\(x\) -1) ⇔ F(\(\dfrac{1}{5}\)) = 0
⇒ 5.(\(\dfrac{1}{5}\))3 + 4.(\(\dfrac{1}{5}\))2 - 6.\(\dfrac{1}{5}\) - a = 0
⇒ \(\dfrac{1}{25}\) + \(\dfrac{4}{25}\) - \(\dfrac{6}{5}\) - a = 0
\(\dfrac{1}{5}\) - \(\dfrac{6}{5}\) - a = 0
- 1 - a = 0
a = - 1
Vậy a = -1 thì 5\(x^3\) + 4\(x^2\) - 6\(x\) - a chia hết cho (5\(x\) - 1)
\(5x^3+4x^2-6x-a⋮5x-1\)
=>\(5x^3-x^2+5x^2-x-5x+1-a-1⋮5x-1\)
=>-a-1=0
=>a+1=0
=>a=-1
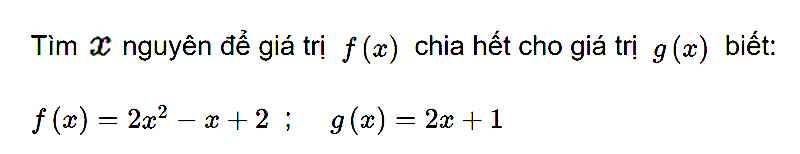

\(f\left(x\right)⋮g\left(x\right)\)
=>\(-2x^3-7x^2-5x+5⋮x+2\)
=>\(-2x^3-4x^2-3x^2-6x+x+2+3⋮x+2\)
=>\(3⋮x+2\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)