Với \(0< x< \sqrt{3}\) ta có đánh giá sau:

\(\dfrac{1}{2-x}\ge\dfrac{x^2+1}{2}\)

Thực vậy, do \(x< \sqrt{3}\Rightarrow2-x>0\), BĐT tương đương:

\(2\ge\left(2-x\right)\left(x^2+1\right)\)

\(\Leftrightarrow x^3-2x^2+x\ge0\)

\(\Leftrightarrow x\left(x-1\right)^2\ge0\) (luôn đúng với \(x>0\))

Áp dụng cho bài toán:

\(\dfrac{1}{2-a}+\dfrac{1}{2-b}+\dfrac{1}{2-c}\ge\dfrac{a^2+1}{2}+\dfrac{b^2+1}{2}+\dfrac{c^2+1}{2}=\dfrac{a^2+b^2+c^2+3}{2}=3\) (đpcm)

Dấu "=" xảy ra khi \(a=b=c=1\)

 Trước khi xem lời giải của mình thì bạn chú ý là trong đó có sử dụng những kí hiệu, thuật ngữ và tính chất khá khó hiểu với học sinh cấp II (thậm chí một vài bạn cấp III cũng chưa chắc đã hiểu thấu). Vì vậy nếu có gì khúc mắc trong lời giải thì bạn cứ nhắn tin riêng cho mình nhé. 

 Trước hết ta đến với các định nghĩa sau:

 Định nghĩa 1: Với điểm X nằm ngoài đường tròn (I), kí hiệu \(d_X\) là đường thẳng nối 2 tiếp điểm của 2 tiếp tuyến qua X ứng với (I).

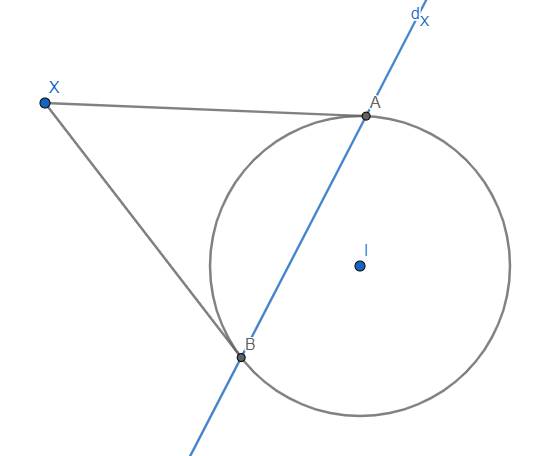
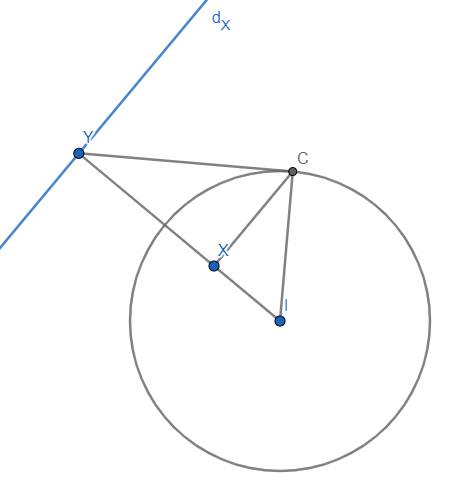
 Định nghĩa 2: Còn với điểm (I) nằm trong đường tròn, nếu lấy điểm Y trên tia IX mà \(IY.IX=R^2\) thì d_X lại là đường thẳng qua Y và vuông góc với IX.

 Định nghĩa 3: Bốn điểm A, B, C, D theo thứ tự nằm trên 1 đường thẳng mà thỏa mãn \(\dfrac{AB}{AD}=\dfrac{CB}{CD}\) thì ta kí hiệu \(\left(BDCA\right)=-1\) và nếu lấy một điểm O bất kì nằm ngoài đường thẳng đó thì ta kí hiệu \(O\left(BDCA\right)=\left(OB,OD,OC,OA\right)=-1\)

 Sau đây là một số tính chất: 

 Tính chất 1: \(d_X\perp IX\), hiển nhiên.

 Tính chất 2: \(Y\in d_X\Leftrightarrow X\in d_Y\) , cũng quá hiển nhiên.

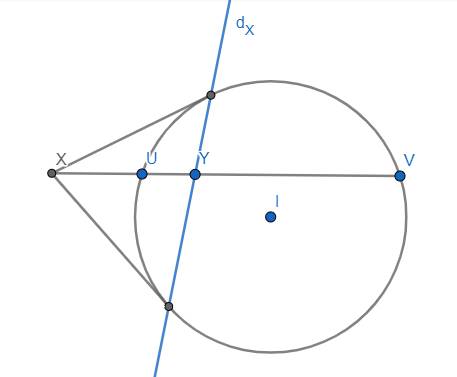
 Tính chất 3: Từ một điểm X nằm ngoài I, vẽ cát tuyến XUV với U, V thuộc (I). Khi đó một điểm Y bất kì thuộc cát tuyến này mà thỏa mãn \(\left(UVYX\right)=-1\) \(\Leftrightarrow Y\in d_X\). 

 Tính chất 4: Cho 4 điểm A, B, C, D theo thứ tự nằm trên đường thẳng d thỏa mãn \(\left(BDCA\right)=-1\) và 1 điểm O nằm ngoài d. Khi đó nếu vẽ 1 đường thẳng d' khác d cắt OA, OB, OC, OD lần lượt tại A', B', C', D' thì \(\left(B'D'C'A'\right)=-1\)

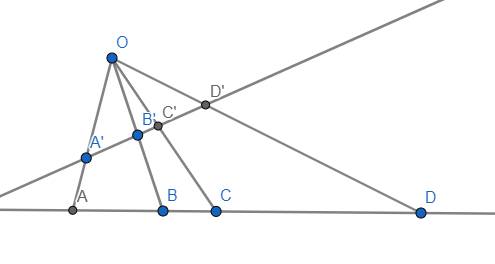
 Tính chất 5: Cho 4 điểm A, B, C, D nằm trên d và một điểm O nằm ngoài d. Khi đó kẻ một đường thẳng song song với một đường bất kì trong số OA, OB, OC, OD và cắt 3 đường còn lại tại M, N, P (N nằm giữa M và P). Khi đó M là trung điểm của NP \(\Leftrightarrow\left(BDCA\right)=-1\)

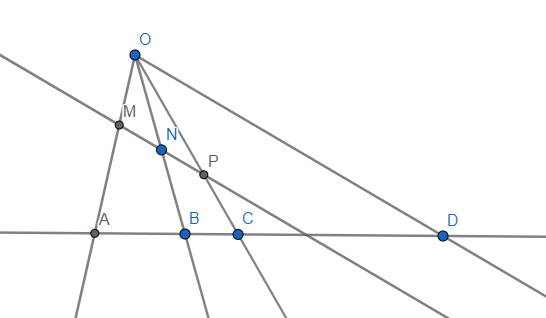
 Quay trở lại bài toán chính.

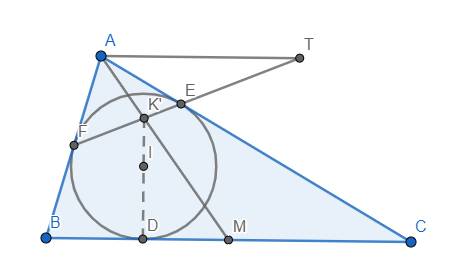
 Gọi M là trung điểm BC, K' là giao điểm của AM và EF. Qua A kẻ đường thẳng song song với BC cắt EF tại T.

 Ta sẽ chứng minh \(K'\equiv K\) hay D, E, K' thẳng hàng.

 Thật vậy, vì AT//BC và M là trung điểm BC nên theo tính chất 5\(\left(AB,AC,AM,AT\right)=-1\). Áp dụng tính chất 4, ta được \(\left(EFK'T\right)=-1\), điều này có nghĩa là \(T\in d_{K'}\) do tính chất 3.

 Hơn nữa, \(K'\in EF\equiv d_A\) nên \(A\in d_{K'}\) (tính chất 2). Do đó \(AT\equiv d_{K'}\) dẫn đến \(IK'\perp AT\) (tính chất 1).

 Do AT//BC nên \(IK'\perp BC\). Mà \(ID\perp BC\) nên D, I, K' thẳng hàng hay \(K'\equiv K\). Ta có đpcm. 

Ta thấy \(10^2!=100!=1.2.3...100\) nên có chữ số tận cùng là 0.

số 0

a)

b)

Một cách tiếp cận là ta sẽ lập công thức tổng quát của dãy \(U_n\):

Ta có \(U_{n+2}=3U_{n+1}-2U_n\)

\(\Leftrightarrow\) \(U_{n+2}-2U_{n+1}=U_{n+1}-2U_n\)

\(\Rightarrow U_{n+2}-2U_{n+1}=U_{n+1}-2U_n=U_n-2U_{n-1}=...=U_1-2U_0=-1\)

Vậy \(U_{n+2}-2U_{n+1}=-1\) hay \(U_{n+1}=2U_n-1\)

\(\Leftrightarrow U_{n+1}-1=2\left(U_n-1\right)\) 

\(\Rightarrow U_n-1=2\left(U_{n-1}-1\right)=4\left(U_{n-2}-1\right)=...=2^n\left(U_0-1\right)=2^n\)

\(\Rightarrow U_n=2^n+1\)

Do đó \(U_{2n}+U_{n+1}-1\)

 \(=2^{2n}+1+2^{n+1}+1-1\)

 \(=\left(2^n\right)^2+2.2^n+1\)

 \(=\left(2^n+1\right)^2\) là số chính phương với mọi \(n\)

Ta có đpcm.

ĐKXĐ: ...

\(\Leftrightarrow x^2+\dfrac{4}{x^2}-4-4\left(x-\dfrac{2}{x}\right)-5=0\)

\(\Leftrightarrow\left(x-\dfrac{2}{x}\right)^2-4\left(x-\dfrac{2}{x}\right)-5=0\)

\(\Leftrightarrow\left(x-\dfrac{2}{x}+1\right)\left(x-\dfrac{2}{x}-5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{2}{x}+1=0\\x-\dfrac{2}{x}-5=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x^2+x-2=0\\x^2-5x-2=0\end{matrix}\right.\)

\(\Rightarrow...\)

"Đây là dạng toán thi HSG casio nên cách giải sẽ được áp dụng trên máy tính nhé"

Ta có quy tắc sau: 

\(S_1=49=\left(2\cdot1^2+5\right)^2\)

\(S_2=S_1+169=S_1+\left(2\cdot2^2+5\right)^2\)

\(S_3=S_1+S_2+529=S_1+S_2+\left(2\cdot3^2+5\right)^2\)

\(S_4=S_1+S_2+S_3+1369=S_1+S_2+S_3+\left(2\cdot4^2+5\right)^2\)

Ta lập trình nhau sau: 

\(X=X+1:A=\left(2\cdot X^2+5\right)^2:X=X+1:B=A+\left(2\cdot X^2+5\right)^2:X=X+1:A=B+\left(2\cdot X^2+5\right)^2\)

Tiếp theo ta ấn phím "CALC" nhập vào `X=0` 

Rồi ấn dấu "=" liên tục cho đến khi `X=15` ta sẽ được \(S_{15}\) và khi `X=25` thì ta được \(S_{25}\)

Vì đa thức \(x^2-1\) có bậc là 2

nên phần dư của phép chia \(P\left(x\right)\) cho \(x^2-1\) có bậc nhỏ hơn 2

Thực hiện phép chia đa thức \(P\left(x\right)\) cho \(\left(x^2-1\right)\), ta được:

\(P\left(x\right)=\left(x^2-1\right)\cdot Q\left(x\right)+ax+b\)

\(=\left(x-1\right)\left(x+1\right)\cdot Q\left(x\right)+ax+b\)

+, Với \(x=1\) thì:

\(P\left(1\right)=\left(1-1\right)\left(1+1\right)\cdot Q\left(1\right)+a\cdot1+b\)

\(\Rightarrow a+b=P\left(1\right)=1^{2010}+1^{2009}+11=13\) (1)

+, Với \(x=-1\) thì:

\(P\left(-1\right)=\left(-1-1\right)\left(-1+1\right)\cdot Q\left(-1\right)+a\cdot\left(-1\right)+b\)

\(\Rightarrow-a+b=P\left(-1\right)=\left(-1\right)^{2010}+\left(-1\right)^{2009}+11=11\) (2)

Từ (1) và (2) suy ra: \(\left\{{}\begin{matrix}a+b=13\\-a+b=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=2\\b=a+11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=12\end{matrix}\right.\)

Vậy phần dư của phép chia \(P\left(x\right)\) cho \(\left(x^2-1\right)\) là \(x+12\)

\(a_0=1\)

\(H=-2a_1+2^2a_2-2^3a_3+2^4a_4-2^5a_5+...+2^{28}a_{28}-2^{29}a_{29}+2^{30}a_{30}\)

\(H+1=1+\left(-2\right)a_1+\left(-2\right)^2a_2+\left(-2\right)^3a_3+\left(-2\right)^4a_4+\left(-2\right)^5a_5+...+\left(-2\right)^{28}a_{28}+\left(-2\right)^{29}a_{29}+\left(-2\right)^{30}a_{30}\)

\(\Leftrightarrow H+1=T\left(-2\right)=5^{15}\)

\(\Rightarrow H=\left[{}\begin{matrix}30517578124\\5^{15}-1\end{matrix}\right.\)