1. Tìm nghiệm nguyên dương của phương trinh x2-2y2-xy –x +5y-6=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi lãi suất mỗi năm của ngân hàng là x(%/năm)
(ĐK: x>0)
Sau 1 năm tổng số tiền (cả gốc lẫn lãi) có được là:
\(150000000\left(1+x\right)\left(đồng\right)\)
Sau 2 năm tổng số tiền (cả gốc lẫn lãi) có được là:
\(150000000\left(1+x\right)\left(1+x\right)=150000000\left(1+x\right)^2\left(đồng\right)\)
Theo đề, ta có:
\(150000000\left(x+1\right)^2=168540000\)
=>\(\left(x+1\right)^2=\dfrac{2809}{2500}\)
=>\(x+1=\dfrac{53}{50}\)
=>\(x=\dfrac{3}{50}=0,06\)(nhận)
=>Lãi suất của ngân hàng đó là 6%/năm

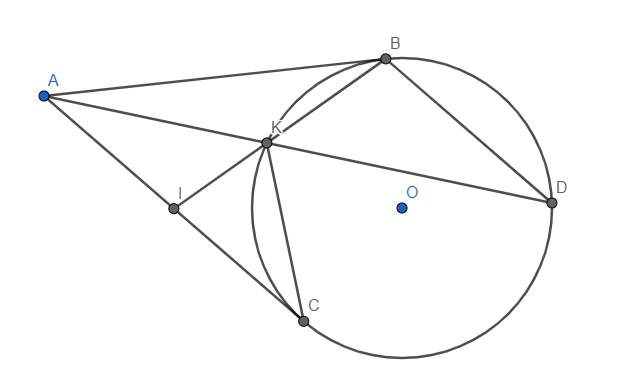
b) Do BD//AC nên \(\widehat{KAI}=\widehat{KDB}\) (2 góc so le trong)
Lại có \(\widehat{ABI}=\widehat{ABK}=\widehat{BDK}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BK.
\(\Rightarrow\widehat{KAI}=\widehat{KBA}\)
c) I là trung điểm AC chứ không phải BC nhé.
Xét tam giác IAK và IBA, ta có:
\(\widehat{AIB}\) chung, \(\widehat{IAK}=\widehat{IBA}\left(cmt\right)\)
\(\Rightarrow\Delta IAK\sim\Delta IBA\left(g.g\right)\)
\(\Rightarrow\dfrac{IA}{IB}=\dfrac{IK}{IA}\)
\(\Rightarrow IA^2=IB.IK\)
\(\Rightarrow IA=IC\) (vì theo câu a, \(IC^2=IB.IK\))
\(\Rightarrow\) I là trung điểm AC.
d) CK vuông góc với đường nào trong đề bài chưa nói nhé.

a: Xét tứ giác MIKC có \(\widehat{MIC}=\widehat{MKC}=90^0\)
nên MIKC là tứ giác nội tiếp
Xét tứ giác MIAH có \(\widehat{MIA}+\widehat{MHA}=90^0+90^0=180^0\)
nên MIAH là tứ giác nội tiếp
Xét tứ giác MKBH có \(\widehat{MKB}+\widehat{MHB}=90^0+90^0=180^0\)
nên MKBH là tứ giác nội tiếp
b: Ta có: MIKC là tứ giác nội tiếp
=>\(\widehat{MIK}+\widehat{MCK}=180^0\)
=>\(\widehat{MIK}=180^0-\widehat{MCB}\)
Ta có: HAIM là tứ giác nội tiếp
=>\(\widehat{MIH}=\widehat{MAH}\)
mà \(\widehat{MAH}=\widehat{MCB}\left(=180^0-\widehat{MAB}\right)\)
nên \(\widehat{MIH}=\widehat{MCB}\)
=>\(\widehat{MIH}+\widehat{MIK}=180^0\)
=>K,I,H thẳng hàng

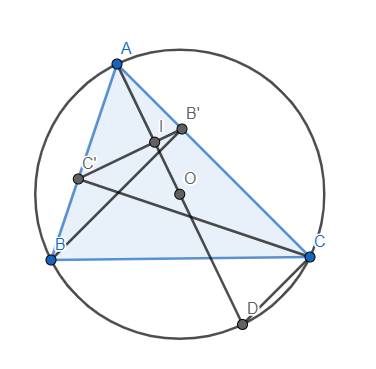
a) Tứ giác BCB'C' có \(\widehat{BC'C}=\widehat{BB'C}=90^o\) nên nó là tứ giác nội tiếp (2 đỉnh kề nhau nhìn cạnh đối diện dưới 2 góc bằng nhau)
b) Vì tứ giác BCB'C' nội tiếp nên \(\widehat{AB'C'}=\widehat{ABC}\) (góc ngoài bằng góc trong đối)
Xét tam giác AB'C' và tam giác ABC có:
\(\widehat{BAC}\) chung và \(\widehat{AB'C'}=\widehat{ABC}\)
\(\Rightarrow\Delta AB'C'\sim\Delta ABC\left(g.g\right)\)
c) Theo câu b), ta có \(\widehat{AB'I}=\widehat{ABC}\)
Lại có \(\widehat{ABC}=\widehat{ADC}\) (góc nội tiếp cùng chắn cung AC)
\(\Rightarrow\widehat{AB'I}=\widehat{ADC}\) \(\Rightarrow\) Tứ giác B'IDC nội tiếp (góc ngoài bằng góc trong đối)
a: Xét tứ giác BC'B'C có \(\widehat{BC'C}=\widehat{BB'C}=90^0\)
nên BC'B'C là tứ giác nội tiếp
b: Ta có: BC'B'C là tứ giác nội tiếp
=>\(\widehat{BC'B'}+\widehat{BCB'}=180^0\)
mà \(\widehat{BC'B'}+\widehat{AC'B'}=180^0\)
nên \(\widehat{AC'B'}=\widehat{ACB}\)
Xét ΔAC'B' và ΔACB có
\(\widehat{AC'B'}=\widehat{ACB}\)
\(\widehat{CAB}\) chung
Do đó: ΔAC'B'~ΔACB


\(\sqrt{3+2\sqrt{2}}-\sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\)
\(=\sqrt{2+2\sqrt{2}+1}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)
\(=\sqrt{\left(\sqrt{2}\right)^2+2\sqrt{2}\cdot1+1^2}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}\right)^2-1^2}}\)
\(=\sqrt{2}+1-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{2-1}}\)
\(=\sqrt{2}+1-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{1}}\)
\(=\sqrt{2}+1-\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=\sqrt{2}+1-\left(\sqrt{2}-1\right)\)
\(=\sqrt{2}+1-\sqrt{2}+1=2\)

Đk: \(x\ge0\)
pt đã cho \(\Leftrightarrow6\sqrt{2x+7}-\left(\dfrac{3}{2}x+\dfrac{33}{2}\right)=2\sqrt{x}-\left(\dfrac{1}{2}x+\dfrac{3}{2}\right)\)
\(\Leftrightarrow\dfrac{36\left(2x+7\right)-\left(\dfrac{3}{2}x+\dfrac{33}{2}\right)^2}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{4x-\left(\dfrac{1}{2}x+\dfrac{3}{2}\right)^2}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)
\(\Leftrightarrow\dfrac{72x+252-\dfrac{9}{4}x^2-\dfrac{99}{2}x-\dfrac{1089}{4}}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{4x-\dfrac{1}{4}x^2-\dfrac{3}{2}x-\dfrac{9}{4}}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)
\(\Leftrightarrow\dfrac{-\dfrac{9}{4}x^2+\dfrac{45}{2}x-\dfrac{81}{4}}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{-\dfrac{1}{4}x^2+\dfrac{5}{2}x-\dfrac{9}{4}}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)
\(\Leftrightarrow\dfrac{x^2-10x+9}{-\dfrac{4}{9}\left(6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\right)}=\dfrac{x^2-10x+9}{-4\left(2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}\right)}\)
\(\Leftrightarrow\left(x^2-10x+9\right)\left[\dfrac{9}{4\left(6+\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\right)}-\dfrac{1}{4\left(2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}\right)}\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-10x+9=0\\\dfrac{9}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{1}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\end{matrix}\right.\)
Với \(x^2-10x+9=0\Leftrightarrow\left(x-1\right)\left(x-9\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=9\end{matrix}\right.\) (nhận)
pt nhỏ thứ 2 \(\Leftrightarrow18\sqrt{x}+\dfrac{9}{2}x+\dfrac{27}{2}=6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\)
\(\Leftrightarrow6\sqrt{2x+7}-18\sqrt{x}=3x-3\)
\(\Leftrightarrow2\sqrt{2x+7}-6\sqrt{x}=x-1\)
\(\Leftrightarrow\dfrac{4\left(2x+7\right)-36x}{2\sqrt{2x+7}+6\sqrt{x}}=x-1\)
\(\Leftrightarrow\dfrac{28-28x}{2\sqrt{2x+7}+6\sqrt{x}}=x-1\)
\(\Leftrightarrow\left(x-1\right)\left(1+\dfrac{28}{2\sqrt{2x+7}+6\sqrt{x}}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\1+\dfrac{28}{2\sqrt{2x+7}+6\sqrt{x}}=0\left(loại\right)\end{matrix}\right.\)
Vậy pt đã cho có tập nghiệm \(S=\left\{1;9\right\}\)


Bài III:
1: ĐKXĐ: y>=-1 và x<>y
\(\left\{{}\begin{matrix}\dfrac{2}{x-y}+\sqrt{y+1}=4\\\dfrac{1}{x-y}-3\sqrt{y+1}=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{6}{x-y}+3\sqrt{y+1}=12\\\dfrac{1}{x-y}-3\sqrt{y+1}=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{7}{x-y}=7\\\dfrac{1}{x-y}-3\sqrt{y+1}=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y=1\\3\sqrt{y+1}=1+5=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y=1\\y+1=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=3\\x=y+1=4\end{matrix}\right.\left(nhận\right)\)
2:
a: Thay m=1 vào (d), ta được:
\(y=x\cdot1-2\cdot1+4=x+2\)
Phương trình hoành độ giao điểm là:
\(x^2=x+2\)
=>\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào y=x+2, ta được:
y=2+2=4
Thay x=-1 vào y=x+2, ta được:
y=-1+2=1
Vậy: (d) cắt (P) tại A(2;4) và B(-1;1)
b: Phương trình hoành độ giao điểm là:
\(x^2=mx-2m+4\)
=>\(x^2-mx+2m-4=0\)
\(\text{Δ}=\left(-m\right)^2-4\cdot1\left(2m-4\right)\)
\(=m^2-8m+16=\left(m-4\right)^2\)
Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0
=>(m-4)2>0
=>\(m-4\ne0\)
=>\(m\ne4\)
Theo Vi-et, ta được:
\(x_1+x_2=-\dfrac{b}{a}=m;x_1x_2=\dfrac{c}{a}=2m-4\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=m^2-2\left(2m-4\right)\)
\(=m^2-4m+8=\left(m-2\right)^2+4>=4\forall m\)
Dấu '=' xảy ra khi m=2

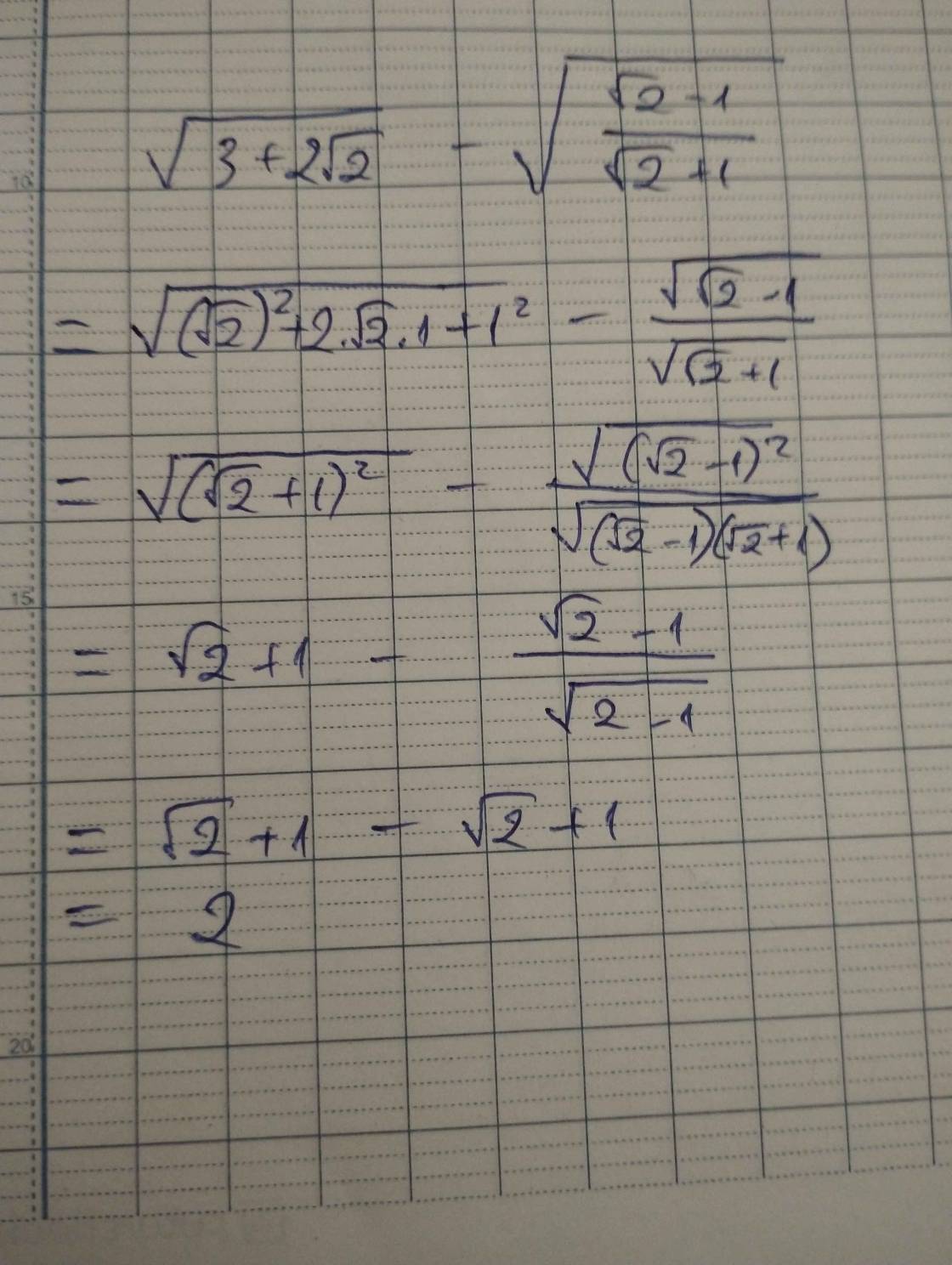
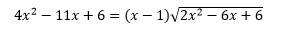

pt đã cho \(\Leftrightarrow x^2-\left(y+1\right)x-2y^2+5y-6=0\) (*)
Ta tính được \(\Delta=9y^2-18y+25>0\) với mọi y.
Để (*) có nghiệm nguyên thì \(9y^2-18y+25\) là số chính phương
\(\Leftrightarrow9y^2-18y+25=z^2\left(z\inℕ,z\ge4\right)\)
\(\Leftrightarrow\left(3y-3\right)^2+16=z^2\)
\(\Leftrightarrow\left(z+3y-3\right)\left(z-3y+3\right)=16\)
Ta có bảng sau:
Vậy \(y=1\) \(\Rightarrow x^2-2x-3=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
Vậy pt đã cho có các nghiệm nguyên là \(\left(-1;1\right)\) và \(\left(3;1\right)\)