mọi người giúp em hai bài này với ạ , thứ sáu em nộp bài rồi
bài 1)Cho a,b là số nguyên ,a>b>0.Chứng minh rằng \(\dfrac{a}{b}\)<\(\dfrac{a+2009}{b+2009}\)
bài 2) Cho a,b,c,d,e,g E Z
b,d,g>0 và ad - bc = 2009
cg - de = 2009
a)so sánh \(\dfrac{a}{b}\);\(\dfrac{c}{d}\);\(\dfrac{e}{g}\)
b)so sánh \(\dfrac{c}{d}\)và \(\dfrac{a+e}{b+g}\)

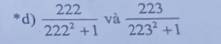

Bài 1:
\(\dfrac{a}{b}-\dfrac{a+2009}{b+2009}=\dfrac{a\left(b+2009\right)-b\left(a+2009\right)}{b\left(b+2009\right)}\)
\(=\dfrac{2009a-2009b}{b\left(b+2009\right)}=\dfrac{2009\left(a-b\right)}{b\left(b+2009\right)}\)
Vì a>b>0 nên a-b>0; b>0; b+2009>0
=>\(\dfrac{2009\left(a-b\right)}{b\left(b+2009\right)}>0\)
=>\(\dfrac{a}{b}>\dfrac{a+2009}{b+2009}\)