a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔBAD=ΔBHD

b: Xét ΔCAB vuông tại A và ΔCAE vuông tại A có

CA chung

AB=AE

Do đó: ΔCAB=ΔCAE

=>\(\widehat{ACB}=\widehat{ACE}\)

=>CA là phân giác của góc ECB

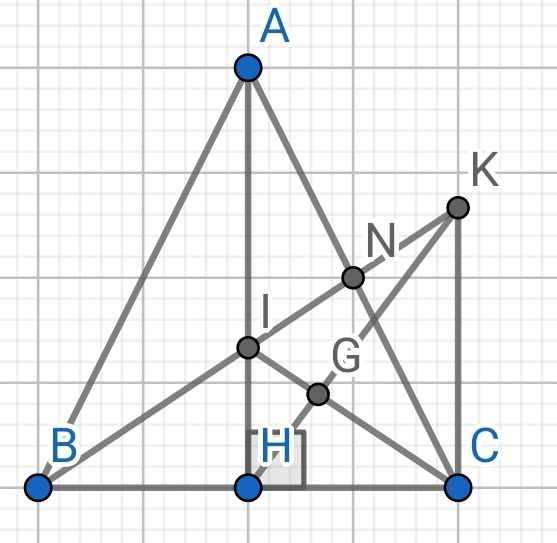
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆AHB và ∆AHC có:

AH là cạnh chung

AB = AC (cmt)

⇒ ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông)

b) Do BN là đường trung tuyến của ∆ABC (gt)

⇒ N là trung điểm của AC

⇒ AN = CN

Do AH // CK (gt)

⇒ ∠IAN = ∠KCN (so le trong)

Xét ∆AIN và ∆CKN có:

∠ANI = ∠CNK (đối đỉnh)

AN = CN (cmt)

∠IAN = ∠KCN (cmt)

⇒ ∆AIN = ∆CKN (g-c-g)

⇒ NI = NK (hai cạnh tương ứng)

c) Xem lại đề. Em viết sai tùm lum

Ta thấy: \(\left\{{}\begin{matrix}\left(3x-2\right)^{2022}\ge0;\forall x\\\left(5y+4\right)^{2024}\ge0;\forall y\end{matrix}\right.\)

\(\Rightarrow\left(3x-2\right)^{2022}+\left(5y+4\right)^{2024}\ge0;\forall x,y\)

\(\Rightarrow\left(3x-2\right)^{2022}+\left(5y+4\right)^{2024}+2023\ge2023;\forall x,y\)

\(\Rightarrow C\ge2023;\forall x,y\)

Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}3x-2=0\\5y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-\dfrac{4}{5}\end{matrix}\right.\)

Vậy \(C_{min}=2023\) tại \(x=\dfrac{2}{3};y=-\dfrac{4}{5}\).

Sửa đề: \(\left(4x^4+14x^3-21x-9\right):\left(2x^2-3\right)\)

\(=\left(4x^4+14x^3+6x^2-6x^2-21x-9\right):\left(2x^2-3\right)\)

\(=\left[\left(4x^4-6x^2\right)+\left(14x^3-21x\right)+\left(6x^2-9\right)\right]:\left(2x^2-3\right)\)

\(=\left[2x^2.\left(2x^2-3\right)+7x.\left(2x^2-3\right)+3.\left(2x^2-3\right)\right]:\left(2x^2-3\right)\)

\(=\left(2x^2+7x+3\right).\left(2x^2-3\right):\left(2x^2-3\right)\)

\(=2x^2+7x+3\)

___________________

\(\left(6x^3-2x^2-9x+3\right):\left(3x-1\right)\)

\(=\left[\left(6x^3-2x^2\right)-\left(9x-3\right)\right]:\left(3x-1\right)\)

\(=\left[2x^2.\left(3x-1\right)-3.\left(3x-1\right)\right]:\left(3x-1\right)\)

\(=\left(2x^2-3\right).\left(3x-1\right):\left(3x-1\right)\)

\(=2x^2-3\)

`#NqHahh`

Lời giải:

Với $n$ nguyên, để $\frac{3n+2}{4n-5}$ là số nguyên thì:

$3n+2\vdots 4n-5$

$\Rightarrow 4(3n+2)\vdots 4n-5$

$\Rightarrow 12n+8\vdots 4n-5$

$\Rightarrow 3(4n-5)+23\vdots 4n-5$

$\Rightarrow 23\vdots 4n-5$

Với $n$ nguyên $\Rightarrow 4n-5\in Ư(23)$
 $\Rightarrow 4n-5\in \left\{-1; -23; 1; 23\right\}$

$\Rightarrow n\in \left\{1; -4,5; 1,5; 7\right\}$

Vì $n$ nguyên nên $n\in\left\{1; 7\right\}$

Bài 4:

a: Dấu hiệu ở đây là số lỗi chính tả trong mỗi bài tiếng Anh của các bạn lớp 7A

b: Có 40 bạn làm bài kiểm tra

c: Bảng tần số:

Nhận xét:

-Đa số các bạn đều sai từ 1 đến 4 lỗi

-Số bạn sai 6 lỗi là ít nhất(1 bạn)

-Số bạn sai 3 lỗi là nhiều nhất(8 bạn)

d: Trung bình cộng là:

\(\overline{X}=\dfrac{1\cdot6+2\cdot6+3\cdot8+4\cdot6+5\cdot5+6\cdot1+7\cdot3+8\cdot2+9\cdot3}{40}\)

=>\(\overline{X}=\dfrac{161}{40}\)

Mốt của dấu hiệu là 3

Bài 9:

a: \(A=\left(\dfrac{1}{3}-\dfrac{8}{15}-\dfrac{1}{7}\right)+\left(\dfrac{2}{3}+\dfrac{-7}{15}+1\dfrac{1}{7}\right)\)

\(=\dfrac{1}{3}-\dfrac{8}{15}-\dfrac{1}{7}+\dfrac{2}{3}+\dfrac{-7}{15}+\dfrac{8}{7}\)

\(=\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\left(-\dfrac{8}{15}-\dfrac{7}{15}\right)+\left(-\dfrac{1}{7}+\dfrac{8}{7}\right)\)

\(=1-1+1=1\)

b: \(B=0,25+\dfrac{3}{5}-\left(\dfrac{1}{8}-\dfrac{2}{5}+1\dfrac{1}{4}\right)\)

\(=0,25+\dfrac{3}{5}-\dfrac{1}{8}+\dfrac{2}{5}-1,25\)

\(=\left(\dfrac{3}{5}+\dfrac{2}{5}\right)+\left(0,25-1,25\right)-\dfrac{1}{8}\)

\(=1-1-\dfrac{1}{8}=-\dfrac{1}{8}\)

c: \(C=\dfrac{3}{4}-\dfrac{4}{5}+\dfrac{5}{6}-\dfrac{6}{7}+\dfrac{7}{8}+\dfrac{6}{7}-\dfrac{5}{6}+\dfrac{4}{5}-\dfrac{3}{4}\)

\(=\left(\dfrac{3}{4}-\dfrac{3}{4}\right)+\left(-\dfrac{4}{5}+\dfrac{4}{5}\right)+\left(\dfrac{5}{6}-\dfrac{5}{6}\right)+\left(-\dfrac{6}{7}+\dfrac{6}{7}\right)+\dfrac{7}{8}\)

\(=0+0+0+0+\dfrac{7}{8}=\dfrac{7}{8}\)

d: \(D=\left(2025-\dfrac{5}{181}+\dfrac{1}{50}\right)-\left(4+\dfrac{3}{181}-\dfrac{2}{50}\right)-\left(1-\dfrac{8}{181}+\dfrac{3}{50}\right)\)

\(=2025-\dfrac{5}{181}+\dfrac{1}{50}-4-\dfrac{3}{181}+\dfrac{2}{50}-1+\dfrac{8}{181}-\dfrac{3}{50}\)

\(=2025-4-1=2020\)

giúp mình với mình đang cần gấp

a: \(\dfrac{-3}{4}+\left(3-\dfrac{1}{4}\right)-\left(2,25-\dfrac{9}{4}\right)\)

\(=-\dfrac{3}{4}+3-\dfrac{1}{4}-\left(2,25-2,25\right)\)

\(=-1+3=2\)

b: \(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{23}+\dfrac{1}{6}\)

\(=\dfrac{1}{2}+\dfrac{1}{6}-\dfrac{1}{3}+\dfrac{1}{23}\)

\(=\dfrac{3+1-2}{6}+\dfrac{1}{23}\)

\(=\dfrac{1}{3}+\dfrac{1}{23}=\dfrac{26}{69}\)

c: \(\left(-\dfrac{13}{7}-\dfrac{4}{9}\right)-\left(-\dfrac{10}{7}-\dfrac{4}{9}\right)\)

\(=-\dfrac{13}{7}-\dfrac{4}{9}+\dfrac{10}{7}+\dfrac{4}{9}\)

\(=-\dfrac{13}{7}+\dfrac{10}{7}=-\dfrac{3}{7}\)

d: \(\dfrac{-14}{12}+0,65-\left(-\dfrac{7}{42}-0,35\right)\)

\(=-\dfrac{7}{6}+0,65+0,35+\dfrac{7}{42}\)

\(=\dfrac{-49}{42}+\dfrac{7}{42}+1=-\dfrac{42}{42}+1=0\)

e: \(\left(\dfrac{7}{8}-\dfrac{5}{2}+\dfrac{4}{7}\right)-\left(-\dfrac{3}{7}+1-\dfrac{13}{8}\right)\)

\(=\dfrac{7}{8}-\dfrac{5}{2}+\dfrac{4}{7}+\dfrac{3}{7}-1+\dfrac{13}{8}\)

\(=\dfrac{20}{8}-\dfrac{5}{2}=\dfrac{5}{2}-\dfrac{5}{2}=0\)

f: \(\dfrac{-3}{7}+\left(3-\dfrac{3}{4}\right)-\left(2,25-\dfrac{10}{7}\right)\)

\(=-\dfrac{3}{7}+2,25-2,25+\dfrac{10}{7}\)

\(=\dfrac{10}{7}-\dfrac{3}{7}=\dfrac{7}{7}=1\)

g: \(\dfrac{1}{2}-\dfrac{43}{101}+\left(-\dfrac{1}{3}\right)-\dfrac{1}{6}\)

\(=\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)-\dfrac{43}{101}\)

\(=\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)-\dfrac{43}{101}=0-\dfrac{43}{101}=-\dfrac{43}{101}\)

h: \(\left(\dfrac{5}{3}-\dfrac{3}{7}+9\right)-\left(2+\dfrac{5}{7}-\dfrac{2}{3}\right)+\left(\dfrac{8}{7}-\dfrac{4}{3}-10\right)\)

\(=\dfrac{5}{3}-\dfrac{3}{7}+9-2-\dfrac{5}{7}+\dfrac{2}{3}+\dfrac{8}{7}-\dfrac{4}{3}-10\)

\(=\left(\dfrac{5}{3}+\dfrac{2}{3}-\dfrac{4}{3}\right)+\left(-\dfrac{3}{7}-\dfrac{5}{7}+\dfrac{8}{7}\right)+\left(9-2-10\right)\)

\(=\dfrac{2}{3}-3=-\dfrac{7}{3}\)

i: \(\dfrac{1}{2}+\dfrac{5}{6}-\dfrac{1}{3}=\dfrac{3}{6}+\dfrac{5}{6}-\dfrac{2}{6}=\dfrac{5+1}{6}=\dfrac{6}{6}=1\)

k: \(\dfrac{1}{2}-\left[\dfrac{3}{8}+\left(-\dfrac{7}{4}\right)\right]\)

\(=\dfrac{1}{2}-\dfrac{3}{8}+\dfrac{7}{4}\)

\(=\dfrac{4}{8}-\dfrac{3}{8}+\dfrac{14}{8}=\dfrac{15}{8}\)

mình cảm ơn nha

\(\dfrac{x+1}{3}=\dfrac{y-2}{4}=\dfrac{z-1}{13}\)

=>\(\dfrac{2x+2}{6}=\dfrac{3y-6}{12}=\dfrac{z-1}{13}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{2x+2}{6}=\dfrac{3y-6}{12}=\dfrac{z-1}{13}=\dfrac{2x-3y+z+2+6-1}{6-12+13}=\dfrac{21+2+5}{7}=4\)

=>\(\left\{{}\begin{matrix}x+1=3\cdot4=12\\y-2=4\cdot4=16\\z-1=13\cdot4=52\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=11\\y=18\\z=53\end{matrix}\right.\)

Lời giải:

$N=\frac{2}{2}+\frac{3}{2^2}+\frac{4}{2^3}+...+\frac{2019}{2^{2018}}$
$2N=2+\frac{3}{2}+\frac{4}{2^2}+....+\frac{2019}{2^{2017}}$

$\Rightarrow 2N-N=2+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2017}}-\frac{2019}{2^{2018}}$

$\Rightarrow N+\frac{2019}{2^{2018}}=2+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2017}}$

$\Rightarrow 2(N+\frac{2019}{2^{2018}})=4+1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2016}}$

$\Rightarrow 2(N+\frac{2019}{2^{2018}})-(N+\frac{2019}{2^{2018}})=3-\frac{1}{2^{2017}}$
$\Rightarrow N+\frac{2019}{2^{2018}}=3-\frac{1}{2^{2017}}$

$N=3-\frac{1}{2^{2017}}-\frac{2019}{2^{2018}}=3-\frac{2021}{2^{2018}}$
Hiển nhiên $\frac{2021}{2^{2018}}$ không phải số nguyên nên $N$ không là số nguyên.