Đây là bài Hình học phẳng thuộc thể loại tương đối khó và TUYỆT HAY. Có thể được dùng làm bài mẫu để dạy các học sinh chuyên toán cách phân tích, tư duy để giải một bài toán Hình học phẳng thuộc dạng "đề bài mông lung" (tức là học trò kg biết bắt đầu từ đâu và phải làm gì).

Nếu trong vòng 1 ngày nữa kg có bạn nào post lời giải lên, tôi sẽ giúp bạn.

 Kẻ trung tuyến AM của tam giác ABC. Qua B kẻ đường thẳng vuông góc với AB cắt AM tại H. Hạ \(DK\perp AM\) tại K. Khi đó H là điểm cố định.

 Vì \(EF=MB=\dfrac{1}{2}BC\) nên \(BF=ME\). Từ đó dễ dàng chứng minh \(\Delta FDB=\Delta MKE\left(c.g.c\right)\) \(\Rightarrow\widehat{DBE}=\widehat{KEB}\). Đồng thời DK//BE nên tứ giác BDKE là hình thang cân \(\Rightarrow\) BDKE là tứ giác nội tiếp.

 Lại có \(\Delta BFD\sim\Delta BMA\) mà \(\Delta BFD=\Delta EMK,\Delta BMA=\Delta CMA\)

 nên \(\Delta EMK\sim\Delta CMA\)

 \(\Rightarrow\widehat{MEK}=\widehat{MCA}\)

 Lại có tứ giác ABHC nội tiếp (do \(\widehat{ABH}=\widehat{ACH}=90^o\)) nên \(\widehat{MCA}=\widehat{BHA}=\widehat{BHK}\)

 Do đó \(\widehat{BEK}=\widehat{BHK}\) \(\Rightarrow\) Tứ giác BHEK nội tiếp.

 Từ đó suy ra 5 điểm B, H, E, K, D cùng thuộc đường tròn (DH). (Trong trường hợp hình vẽ mà \(\widehat{BEK}+\widehat{BHK}=180^o\) thì cũng chứng minh được 5 điểm đó cùng thuộc đường tròn (DH))

 \(\Rightarrow\widehat{DEH}=90^o\)

 \(\Rightarrow\) đường thẳng qua E vuông góc với DE đi qua điểm H cố định. Ta có đpcm.

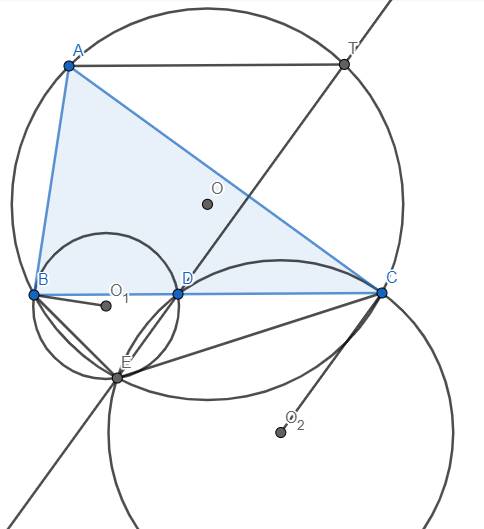
a) Xét đường tròn (O₁) có AB tiếp xúc với (O₁) tại B nên \(\widehat{ABD}=\widehat{BED}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn \(\stackrel\frown{BD}\))

 Tương tự, ta có \(\widehat{ACD}=\widehat{DEC}\)

 Cộng theo vế 2 đẳng thức vừa tìm được, ta có:

 \(\widehat{ABD}+\widehat{ACD}=\widehat{BEC}\)

 \(\Rightarrow180^o-\widehat{BAC}=\widehat{BEC}\)

 \(\Rightarrow\widehat{BEC}+\widehat{BAC}=180^o\)

 \(\Rightarrow\) Tứ giác ABEC nội tiếp đường tròn (đpcm)

b) Gọi T là giao điểm của DE với (O)

Trong đường tròn (O₂), ta có \(\widehat{BDE}=180^o-\widehat{CDE}=180^o-\dfrac{sđ\stackrel\frown{CE}_{lớn}}{2}\) \(=\dfrac{360^o-sđ\stackrel\frown{CE}_{lớn}}{2}\) \(=\dfrac{sđ\stackrel\frown{CE}_{nhỏ}}{2}\)  \(=\widehat{ACE}\)

 Trong đường tròn (O), ta có \(\widehat{ACE}=\dfrac{sđ\stackrel\frown{AE}}{2}\)

 Lại có \(\widehat{BDE}=\dfrac{sđ\stackrel\frown{BE}+sđ\stackrel\frown{CT}}{2}\) 

\(\Rightarrow\dfrac{sđ\stackrel\frown{AE}}{2}=\dfrac{sđ\stackrel\frown{BE}+sđ\stackrel\frown{CT}}{2}\)

 \(\Rightarrow sđ\stackrel\frown{AB}=sđ\stackrel\frown{CT}\)

 \(\Rightarrow\) AT//CB

 Do đó T là điểm cố định \(\Rightarrow\) DE đi qua T cố định.

Bạn vào trang cá nhân của mình xem trả lời nhé.

Diện tích xung quanh thùng nước là:

\(2\Omega\cdot15\cdot25=750\Omega\left(cm^2\right)\)

Diện tích 1 mặt là \(15^2\cdot\Omega=225\Omega\left(cm^2\right)\)

Diện tích tôn cần dùng là \(750\Omega+225\Omega=975\Omega\left(cm^2\right)\)

Diện tích xung quanh thùng:

2π.15.25 = 750π (cm²)

Diện tích đáy thùng:

π.15² = 225π (cm²)

Diện tích tôn cần dùng:

750π + 2.225π = 1200π (cm²)

10³³ = 100..00 (33 chữ số 0)

Biểu thức B là biểu thức nào hả bạn?

Và bạn xem lại chỗ cuối của A là $2x-4$ hay $2x-8$

a: Sửa đề: Đường tròn tâm O' đường kính BH

Xét (O) có

ΔHMA nội tiếp

HA là đường kính

Do đó: ΔHMA vuông tại M

=>HM\(\perp\)CA tại M

Xét (O') có

ΔBNH nội tiếp

BH là đường kính

Do đó: ΔBNH vuông tại N

=>HN\(\perp\)BC tại N

Xét tứ giác CMHN có \(\widehat{CMH}=\widehat{CNH}=\widehat{MCN}=90^0\)

nên CMHN là hình chữ nhật

b: Ta có: CMHN là hình chữ nhật

=>\(\widehat{CMN}=\widehat{CHN}\)

mà \(\widehat{CHN}=\widehat{B}\left(=90^0-\widehat{NCH}\right)\)

nên \(\widehat{CMN}=\widehat{B}\)

mà \(\widehat{CMN}+\widehat{AMN}=180^0\)(hai góc kề bù)

nên \(\widehat{AMN}+\widehat{B}=180^0\)

=>AMNB nội tiếp

a: Sau t giờ thì An đi được 30t(km)

=>Khoảng cách từ Hà Nội đến vị trí của An sau t giờ là:

d=150-30t

Sau t giờ thì Bình đi được 45t(km)

=>Khoảng cách từ Hà Nội đến vị trí của Bình sau t giờ là:

f=150-45t

b: Để khoảng cách giữa 2 người là 30km thì:

150-30t=150-45t+30 hoặc 150-30t+30=150-45t

=>150-30t=180-45t hoặc 180-30t=150-45t

=>15t=30 hoặc 15t=-30

=>t=2 hoặc t=-2(loại)

=>Sau 2 giờ kể từ khi hai người cùng xuất phát thì khoảng cách giữa 2 người là 30km

dạ, em cảm ơn nhiều ạ
@Nguyễn Lê Phước Thịnh

Bạn post cái đề còn sai thì ai giúp được cho bạn?