a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có

\(\widehat{ABH}\) chung

Do đó: ΔABH~ΔCBA

=>\(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)

=>\(AB^2=BH\cdot BC\)

b: Xét ΔAEH vuông tại E và ΔAHB vuông tại H có

\(\widehat{EAH}\) chung

Do đó: ΔAEH~ΔAHB

=>\(\dfrac{AE}{AH}=\dfrac{AH}{AB}\)

=>\(AH^2=AE\cdot AB\left(1\right)\)

Xét ΔAFH vuông tại F và ΔAHC vuông tại H có

\(\widehat{FAH}\) chung

DO đó: ΔAFH~ΔAHC

=>\(\dfrac{AF}{AH}=\dfrac{AH}{AC}\)

=>\(AH^2=AF\cdot AC\left(2\right)\)

Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)

c: \(AE\cdot AB=AF\cdot AC\)

=>\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)

Xét ΔAEF vuông tại A và ΔACB vuông tại A có

\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)

Do đó: ΔAEF~ΔACB

a: Xét ΔMAN vuông tại A và ΔMBP vuông tại B có

\(\widehat{AMN}\) chung

Do đó: ΔMAN~ΔMBP

b: Xét ΔHBN vuông tại B và ΔHAP vuông tại A có

\(\widehat{BHN}=\widehat{AHP}\)(hai góc đối đỉnh)

Do đó; ΔHBN~ΔHAP

=>\(\dfrac{HB}{HA}=\dfrac{HN}{HP}\)

=>\(HB\cdot HP=HA\cdot HN\)

c: Ta có: NA\(\perp\)MP

PI\(\perp\)MP

Do đó: NA//PI

=>NH//PI

ta có: PH\(\perp\)MN

NI\(\perp\)MN

Do đó: PH//NI

Xét tứ giác NHPI có

NH//PI

HP//NI

Do đó: NHPI là hình bình hành

=>NP cắt HI tại trung điểm của mỗi đường

mà K là trung điẻm của NP

nên K là trung điểm của HI

=>H,K,I thẳng hàng

Lời giải:

a.

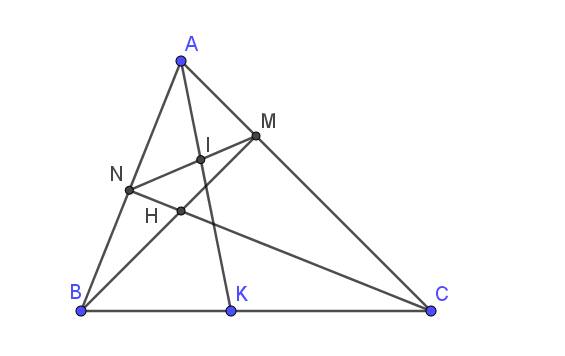
Xét tam giác $ANC$ và $AMB$ có:

$\widehat{A}$ chung

$\widehat{ANC}=\widehat{AMB}=90^0$

$\Rightarrow \triangle ANC\sim \triangle AMB$ (g.g)

$\Rightarrow \frac{AN}{AM}=\frac{AC}{AB}$

Xét tam giác $AMN$ và $ABC$ có:

$\widehat{A}$ chung

$\frac{AN}{AM}=\frac{AC}{AB}$ (cmt) 

$\Rightarrow \triangle AMN\sim \triangle ABC$ (c.g.c)

b.

Từ phần a thì  $\frac{AN}{AM}=\frac{AC}{AB}\Rightrrow \frac{AM}{AN}=\frac{AB}{AC}(1)$

Áp dụng tính chất đường phân giác ta có:

$\frac{IM}{IN}=\frac{AM}{AN}(2)$

$\frac{KB}{KC}=\frac{AB}{AC}(3)$

Từ $(1); (2); (3)\Rightarrow \frac{IM}{IN}=\frac{KB}{KC}$

Hình vẽ:

a: Xét tứ giác AIHK có \(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)

nên AIHK là hình chữ nhật

b: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có

\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)

Do đó: ΔAHB~ΔCHA

=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)

=>\(HA^2=HB\cdot HC\)

c: Ta có: AIHK là hình chữ nhật

=>\(\widehat{AIK}=\widehat{AHK}\)

mà \(\widehat{AHK}=\widehat{C}\left(=90^0-\widehat{CAH}\right)\)

nên \(\widehat{AIK}=\widehat{ACB}\)

Xét ΔAIK vuông tại A và ΔACB vuông tại A có

\(\widehat{AIK}=\widehat{ACB}\)

Do đó: ΔAIK~ΔACB

d: ΔABC vuông tại A

mà AM là đường trung tuyến

nên AM=MC

=>\(\widehat{MAC}=\widehat{MCA}\)

\(\widehat{AKI}+\widehat{MAC}=\widehat{MCA}+\widehat{B}=90^0\)

=>AM\(\perp\)IK tại D

                    Giải:

Gọi chiều rộng của hình chữ nhật là \(x\) (m); \(x\) > 0

Chiều dài của hình chữ nhật là: \(x\times\) 3 = 3\(x\)

Nếu tăng chiều dài của hình chữ nhật thêm 3m thì chiều dài lúc sau là:

          3\(x\) + 3 (m)

Nếu tăng chiều rộng của hình chữ nhật thêm 2m thì chiều rộng của hình chữ nhật lúc sau là: \(x\) - 2 (m)

Diện tích của hình chữ nhật lúc đầu là: 3\(x\) \(\times\)\(x\) = 3\(x^2\) (m²)

Diện tích của hình chữ nhật lúc sau là:

       (3\(x\) + 3)(\(x\) - 2) = 3\(x^2\)- 3\(x\) - 6 (m²)

Theo bài ra ta có phương trình:

      3\(x^2\) - (3\(x^2\) - 3\(x\) - 6) = 90

     3\(x^2\) - 3\(x^2\) + 3\(x\) + 6  = 90

                        3\(x\) + 6 = 90

                       3\(x\)        = 90 - 6

                       3\(x\)        = 84 

                         \(x\)         = 84 : 3

                         \(x\)         = 28

Vậy chiều rộng của hình chữ nhật là 28 m

Chiều dài của hình chữ nhật là: 28 x 3  = 84 (m)

Kết luận: Chiều rộng của hình chữ nhật là 28 m

              Chiều dài của hình chữ nhật là 84 m

Gọi độ dài quãng đường AB là x(km)

(ĐK: x>0)

Thời gian dự kiến sẽ đi hết quãng đường là \(\dfrac{x}{50}\left(giờ\right)\)

Thời gian đi 2/3 quãng đường đầu tiên là:

\(\dfrac{x\cdot\dfrac{2}{3}}{50}=\dfrac{2x}{3}:50=\dfrac{2x}{150}=\dfrac{x}{75}\left(giờ\right)\)

Thời gian đi 1/3 quãng đường còn lại là:

\(\dfrac{x\cdot\dfrac{1}{3}}{40}=\dfrac{x}{3}:40=\dfrac{x}{120}\left(giờ\right)\)

Ô tô đến B chậm hơn dự kiến 30p=0,5 giờ nên ta có:

\(\dfrac{x}{120}+\dfrac{x}{75}-\dfrac{x}{50}=0,5\)

=>\(\dfrac{5x+8x-12x}{600}=0,5\)

=>\(\dfrac{x}{600}=0,5\)

=>\(x=600\cdot0,5=300\left(nhận\right)\)

Vậy: Độ dài quãng đường AB là 300km

Lời giải:

Để dung dịch đó có nồng độ 20% thì lượng nước muối là:

$150:20\text{%}=750$ (gam)

Cần thêm vào dung dịch đó số gam nước là:

$750-500=250$ (gam)

giải: (cái này là cách suy luận thôi chứ cách giải thì đây cũng chịu)

gọi x là tổng điểm An có được từ những câu trả lời đúng ; x là stn khác 0; x chia hết cho 5; 0<x<250

vì tổng điểm cuối cùng của An là số chẵn, số điểm bị trừ cũng là số chẵn => x : 2 

mà (2:5) = 1 => x chia hết cho 10 

gọi y là số điểm An đã bị trừ; y là stn khác 0, y chia hết cho 2; 0<y<100

ta có: x - y = 194 (a, b là hằng số khác 0; a,b thuộc Z+)

mà x có tận cùng là 0

=> y có chữ số tận cùng là 6 => y thuộc {6;16;26;36;46)

xét từng TH:
TH1: y = 6 => số câu sai là 3 => số câu đúng là 47 => x=47.5=235 (KTM)

TH2: y=16 => số câu sai là 8 => số câu đúng là 42 => x=42.5=210

x - y = 194

210 - 16 = 194 (TM)

TH3: y=26 => số câu sau là 13 => số câu đúng là 37 => x=37.5 185 (KTM)

tiến tục...... (thật ra thì đếm đoạn thỏa mãn ở TH2 rồi thì chẳng  cần tìm tiếp nữa:))

vậy số câu đúng là 42

Gọi số câu hỏi An đã trả lời đúng là x(câu)

(ĐK: \(x\in Z^+\))

Số câu An làm sai là 50-x(câu)

Số điểm An được cộng là 5x(điểm)

Số điểm An bị trừ là 2(50-x)(điểm)

Theo đề, ta có:

5x-2(50-x)=194

=>7x-100=194

=>7x=294

=>x=294:7=42(nhận)

Vậy: Số câu An trả lời đúng là 42 câu

Gọi số áo mà tổ cần may theo kế hoạch là x(chiếc), x € N*

Vì ban đầu, tổ có ý định may 30 chiếc áo mỗi ngày nên thời gian dự định hoàn thành kế hoạch là x/30(ngày)

Thực tế tổ đã may thêm 20 chiếc áo nữa nên số áo tổ đã may được là x+20(chiếc)

Vì thực tế mỗi ngày may được 40 chiếc áo nên thời gian tổ đã may áo là x+20/40(ngày)

Vì tổ hoàn thành kế hoạch sớm hơn 3 ngày nên ta có phương trình:

x/30 - x+20/40=3

4x/120-3(x+20)/120=360/120

4x/120-3x+60/120=360/120

4x-(3x+60)=360

4x-3x-60=360

4x-3x=360+60

x=420(Thoả mãn điều kiện)

Vậy theo kế hoạch tổ cần may 420 chiếc áo