Dirichlet à:))?

Trong 3 số dương a,b,c tồn tại ít nhất 2 số cùng nhỏ hơn hoặc không nhỏ hơn 1

G/s 2 số đó là a và b

Khi đó: \(\left(1-a\right)\left(1-b\right)\ge0\Leftrightarrow ab-a-b+1\ge0\)

\(\Leftrightarrow ab\ge a+b-1\Leftrightarrow2abc\ge2ca+2bc-2c\)

\(\Rightarrow a^2+b^2+c^2+2abc+1\ge a^2+b^2+c^2+2ca+2bc-2c+1\)

Mà \(\left(a^2+b^2+c^2+2ca+2bc-2c+1\right)-2\left(ab+bc+ca\right)\)

\(=\left(a^2-2ab+b^2\right)+\left(c^2-2c+1\right)=\left(a-b\right)^2+\left(c-1\right)^2\ge0\left(\forall a,b,c\right)\)

\(\Rightarrow a^2+b^2+c^2+2ca+2bc-2c+1\ge2\left(ab+bc+ca\right)\)

\(\Rightarrow a^2+b^2+c^2+2abc+1\ge2\left(ab+bc+ca\right)\)

Dấu "=" xảy ra khi: a = b = c = 1

Theo nguyên lý Dirichlet, ta thấy rằng trong ba số a,b,c sẽ có hai số hoặc cùng ≥1 hoặc cùng ≤1. Giả sử hai số đó là a,b khi đó:
(a−1)(b−1)≥0.
Từ đây, bằng cách sử dụng hằng đẳng thức:
a2+b2+c2+2abc+1−2(ab+bc+ca)=(a−b)2+(c−1)2+2c(a−1)(b−1)≥0
Ta thu được ngay bất đẳng thức (1), phép chứng minh hoàn tất.

Search mạng!!

1) Thay \(x=16\)vào B ta đc

\(\frac{16-\sqrt{16}}{\sqrt{16}-2}=6\)

Vậy B =6 với x=16

2)\(A=\frac{\sqrt{x}+1}{\sqrt{x}+2}+\frac{\sqrt{x}}{2-\sqrt{x}}-\frac{2\sqrt{x}+8}{x-4}\)

\(=\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{x-4}-\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{x-4}-\frac{2\sqrt{x}+8}{x-4}\)

\(=\frac{x-\sqrt{x}-2}{x-4}-\frac{x+2\sqrt{x}}{x-4}-\frac{2\sqrt{x}+8}{x-4}\)

\(=\frac{-5\sqrt{x}-10}{x-4}\)

\(=\frac{-5\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\frac{-5}{\sqrt{x}-2}\)

3) Để \(B-A< 0\)\(\Leftrightarrow\frac{x-\sqrt{x}}{\sqrt{x}-2}-\frac{-5}{\sqrt{x}-2}< 0\)

\(\Leftrightarrow\frac{x-\sqrt{x}+5}{\sqrt{x}-2}< 0\)

 \(\Leftrightarrow\hept{\begin{cases}x-\sqrt{x}+5>0\\\sqrt{x}-2< 0\end{cases}}\)( vì \(x-\sqrt{x}+5>0;\forall x\))

\(\Leftrightarrow x< 4\) Kết hợp với điều kiện đề bài

\(\Rightarrow0\le x< 4\) Mà x nguyên

\(\Rightarrow x\in\left\{0;1;2;3\right\}\)

Vậy ...

Lời giải:

a) Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:

Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)

⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)

b) Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)

Vậy OC = 25 cm

OC=25cm

cùng chiều

Cùng chiều kim đồng hồ

Tâm $O$ là giao điểm của đường vuông góc với $d$ tại $A$ và đường trung trực của $AB$. Dựng đường tròn $(O;OA)$.

Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A. Suy ra tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.

Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.

Tam giác $ABC$ có:

$A{B}^2+A{C}^2=3^2+4^2=5^2$

Mặt khác: $B{C}^2=5^2$

Vậy ${\mathrm{A}\mathrm{B}}^2+{\mathrm{A}\mathrm{C}}^2={\mathrm{B}\mathrm{C}}^2$.

Do đó $\widehat{BAC}=90^{\circ }$ (định lí Py-ta-go đảo).

$CA$ vuông góc với bán kính $BA$ tại $A$ nên $CA$ là tiếp tuyến của đường tròn $(B)$.

tam giác ABC

\(=\sqrt{64}=8\left(cm\right)\)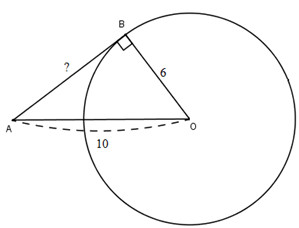

Áp dụng định lý Pytago vào tam giác AOB vuông tại B, ta có:

AB=\(\sqrt{AO^2-OB^2}=\sqrt{10^2-6^2}\)\(=\sqrt{64}=8\left(cm\right)\)

AB=8

a) vẽ bạn tự vẽ nha

b) Xét pt hoành độ giao điểm chung của (d) và (P) ta có:
\(\frac{1}{4}x^2=x+m\)

\(\Leftrightarrow x^2-4x-4m=0\left(1\right)\)

\(\Delta^,=4+4m\)

Để (d) tiếp xúc với (P) \(\Leftrightarrow\Delta^,=0\)

\(\Leftrightarrow4+4m=0\)

\(\Leftrightarrow m=-1\)

Thay m=-1 vào pt (1) ta được : 

\(x^2-4x+4=0\)

\(\Leftrightarrow\left(x-2\right)^2=0\)

\(\Leftrightarrow x=2\)

\(\Rightarrow y=\frac{1}{4}.2^2=1\)

Gọi tọa độ tiếp điểm của (d) tiếp xúc với (P) là A(x,y) 

=> tọa độ tiếp điểm là \(A\left(2;1\right)\)