\(f\left(x\right)=-x^2+1\)

=>\(f'\left(x\right)=-2x\)

\(f\left(-2\right)=-\left(-2\right)^2+1=-4+1=-3\)

\(f'\left(-2\right)=-2\cdot\left(-2\right)=4\)

Phương trình tiếp tuyến của (P) tại x=-2 là:

y-f(-2)=f'(-2)(x+2)

=>y-(-3)=4(x+2)=4x+8

=>y=4x+8-3=4x+5

a: ΔABC đều

mà AI là đường trung tuyến

nên AI\(\perp\)BC

ta có: BC\(\perp\)AI

BC\(\perp\)SA(SA\(\perp\)(ABC))

SA,AI cùng thuộc mp(SAI)

Do đó: BC\(\perp\)(SAI)

b: Vì ΔABC đều nên \(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)

\(V_{S.ABCD}=\dfrac{1}{3}\cdot SA\cdot S_{ABC}=\dfrac{1}{3}\cdot\dfrac{a^2\sqrt{3}}{4}\cdot2a=\dfrac{a^3\sqrt{3}}{6}\)

a: Ta có: BD\(\perp\)AC(ABCD là hình vuông)

BD\(\perp\)SA(SA\(\perp\)(ABCD))

SA,AC cùng thuộc mp(SAC)

Do đó: BD\(\perp\)(SAC)

b: BC\(\perp\)AB(ABCD là hình vuông)

BC\(\perp\)SA(SA\(\perp\)(ABCD))

SA,AB cùng thuộc mp(SAB)

Do đó: BC\(\perp\)(SAB)

c: DC\(\perp\)AD(ABCD là hình vuông)

DC\(\perp\)SA(SA\(\perp\)(ABCD))

AD,SA cùng thuộc mp(SAD)

Do đó: DC\(\perp\)(SAD)

Số học sinh thích ít nhất 1 môn bóng rổ hoặc bóng chuyền là:

\(45-5=40\)

Số học sinh thích cả bóng rổ và bóng chuyền là:

\(25+20-40=5\) 

Xác suất để học sinh đó thích cả 2 môn:

\(P=\dfrac{C_5^1}{C_{45}^1}=\dfrac{1}{9}\)

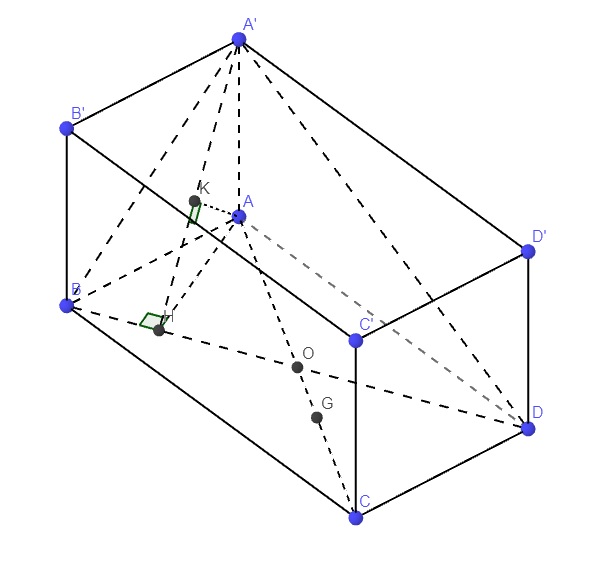
Gọi O là giao điểm AC và BD \(\Rightarrow O\) là trung điểm BD và AC

Do G là trọng tâm tam giac BCD \(\Rightarrow OG=\dfrac{1}{3}OC=\dfrac{1}{3}OA\)

Mà \(GA\cap\left(A'BD\right)=O\Rightarrow d\left(G;\left(A'BD\right)\right)=\dfrac{1}{3}d\left(A;\left(A'BD\right)\right)\)

Trong mp (ABCD), từ A kẻ \(AH\perp BD\) 

Trong mp (A'AH), từ A kẻ \(AK\perp A'H\)

\(\Rightarrow AK\perp\left(A'BD\right)\Rightarrow AK=d\left(A;\left(A'BD\right)\right)\)

Hệ thức lượng tam giác vuông ABD:

\(AH=\dfrac{AB.AD}{\sqrt{AB^2+AD^2}}=\dfrac{2a\sqrt{5}}{5}\)

Hệ thức lượng trong tam giác vuông A'AH:

\(AK=\dfrac{A'A.AH}{\sqrt{A'A^2+AH^2}}=\dfrac{2a}{3}\)

\(\Rightarrow d\left(G;\left(A'BD\right)\right)=\dfrac{1}{3}AK=\dfrac{2a}{9}\)

b: S.ABCD là hình chóp tứ giác đều

O là tâm của đáy ABCD

Do đó: SO\(\perp\)(ABCD)

\(\widehat{SA;\left(ABCD\right)}=\widehat{AS;AO}=\widehat{SAO}\)

ABCD là hình vuông

=>\(AC=\sqrt{AB^2+BC^2}=\sqrt{\left(a\sqrt{6}\right)^2+\left(a\sqrt{6}\right)^2}=2a\sqrt{3}\)

O là trung điểm của AC

=>\(AO=\dfrac{AC}{2}=a\sqrt{3}\)

Xét ΔSOA vuông tại O có \(tanSAO=\dfrac{SO}{OA}=\dfrac{2a}{a\sqrt{3}}=\dfrac{2}{\sqrt{3}}\)

nên \(\widehat{SAO}\simeq49^06'\)

=>\(\widehat{SA;\left(ABCD\right)}\simeq49^06'\)

c: Ta có: DA\(\perp\)AB

DA\(\perp\)AC

AB,AC cùng thuộc mp(ABC)

Do đó: DA\(\perp\)(ABC)

\(\widehat{DB;\left(ABC\right)}=\widehat{BD;BA}=\widehat{DBA}\)

Xét ΔDAB vuông tại A có \(tanDBA=\dfrac{DA}{AB}=\dfrac{2a}{2a}=1\)

nên \(\widehat{DBA}=45^0\)

=>\(\widehat{DB;\left(ABC\right)}=45^0\)

d: DA\(\perp\)AB

DA\(\perp\)AC

AB,AC cùng thuộc mp(ABC)

Do đó: DA\(\perp\)(ABC)

\(\widehat{DC;\left(ABC\right)}=\widehat{CD;CA}=\widehat{DCA}\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC=\sqrt{\left(a\sqrt{5}\right)^2-\left(a\right)^2}=2a\)

Xét ΔDAC vuông tại A có \(tanDCA=\dfrac{DA}{AC}=\dfrac{1}{2}\)

nên \(\widehat{DCA}\simeq26^034'\)

=>\(\widehat{DC;\left(ABC\right)}\simeq26^034'\)