Cho p: y= x² d: y= (2k+1)x - 4k + 2 Tìm k để y1² + x2² = 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=11\\x_1x_2=\dfrac{c}{a}=1\end{matrix}\right.\)
\(Q=\left(x_1-x_2\right)^2+x_2\left|x_2-11\right|\)
\(=\left(x_1+x_2\right)^2-4x_1x_2+x_2\cdot\left|x_2-x_1-x_2\right|\)
\(=\left(x_1+x_2\right)^2-4x_1x_2\pm x_2x_1\)
\(=11^2-4\cdot1\pm1=117\pm1=\left[{}\begin{matrix}116\\118\end{matrix}\right.\)

ĐKXĐ: x>0
\(log_4\left(2x+3\right)-3=log_4x\)
=>\(log_4\left(2x+3\right)=log_4x+3=log_4x+log_464=log_4\left(64x\right)\)
=>2x+3=64x
=>-62x=-3
=>\(x=\dfrac{3}{62}\)(nhận)

Gọi vận tốc của dòng nước là x(km/h)
(Điều kiện: 0<x<14)
Vận tốc lúc đi là 14+x(km/h)
vận tốc lúc về là 14-x(km/h)
Thời gian đi là \(\dfrac{32}{14+x}\left(giờ\right)\)
Thời gian về là \(\dfrac{32}{14-x}\left(giờ\right)\)
Tổng thời gian cả đi và về là 4h40p=14/3 giờ nên ta có:
\(\dfrac{32}{14+x}+\dfrac{32}{14-x}=\dfrac{14}{3}\)
=>\(\dfrac{16}{14+x}+\dfrac{16}{14-x}=\dfrac{7}{3}\)
=>\(\dfrac{16\left(14-x\right)+16\left(14+x\right)}{196-x^2}=\dfrac{7}{3}\)
=>\(\dfrac{448}{196-x^2}=\dfrac{7}{3}\)
=>\(196-x^2=448\cdot\dfrac{3}{7}=192\)
=>\(x^2=4\)
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
Vậy: vận tốc của dòng nước là 2km/h

Lời giải:
$\sqrt[13]{16}+4=\sqrt[13]{16}+4$, không thu gọn được bạn nhé.

a: \(H=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{2}{a-4}\right)\cdot\left(\sqrt{a}-1+\dfrac{\sqrt{a}-4}{\sqrt{a}}\right)\)
\(=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\right)\cdot\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)+\sqrt{a}-4}{\sqrt{a}}\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}+2\right)-2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\cdot\dfrac{a-4}{\sqrt{a}}\)
\(=\dfrac{a+3\sqrt{a}}{\sqrt{a}}=\sqrt{a}+3\)
b: H=a+3
=>\(a+3=\sqrt{a}+3\)
=>\(a-\sqrt{a}=0\)
=>\(\sqrt{a}\left(\sqrt{a}-1\right)=0\)
=>\(\left[{}\begin{matrix}a=0\left(loại\right)\\a=1\left(nhận\right)\end{matrix}\right.\)

Áp dụng BĐT Cô-si:
\(\sqrt{3x+2y+z}+\sqrt{3y+2z+x}+\sqrt{3z+2x+y}\)
\(=\dfrac{1}{2\sqrt{6}}.\left(2.\sqrt{6}.\sqrt{3x+2y+z}+2.\sqrt{6}.\sqrt{3y+2z+x}+2.\sqrt{6}.\sqrt{3z+2x+y}\right)\)
\(\le\dfrac{1}{2\sqrt{6}}\left(6+3x+2y+z+6+3y+2z+x+6+3z+2x+y\right)\)
\(=\dfrac{1}{2\sqrt{6}}\left(6x+6y+6z+18\right)=\dfrac{36}{2\sqrt{6}}=3\sqrt{6}\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=1\)
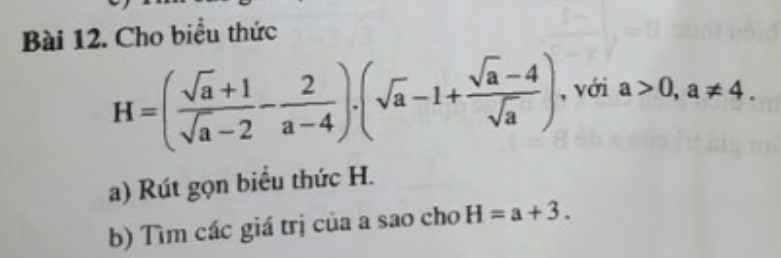
Tìm $k$ để $y_1^2+x_2^2=7$ hay $x_1^2+x_2^2=7$ vậy bạn?
À y1² + x1=7 mới đúng ah