So sánh hai số bằng cách vận dụng hằng đẳng thức: A = 216 và B (2 +1)(22 +1)(24 +1)(28 +1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(xyz\le\frac{\left(x+y\right)^2z}{4}=\frac{\left(6-z\right)^2z}{4}=\frac{\left(6-z\right)\left[\left(6-z\right)z\right]}{4}\)
\(\le\frac{\left(6-z\right)\left(6-z+z\right)^2}{16}=\frac{\left(6-z\right).36}{16}\le\frac{\left(6-3\right).36}{16}=\frac{27}{4}\)
Dấu \(=\)khi \(\hept{\begin{cases}x=y\\z=3\\x+y+z=6\end{cases}}\Leftrightarrow\hept{\begin{cases}x=y=\frac{3}{2}\\z=3\end{cases}}\).

HF là đường trung bình tam giác ABC
=> AB=2HF
hay x=2.1=2(cm)
EH là đường trung bình tam giác ADC
=>EH=1/2DC
hay y=1/2.4=2(cm)

\(\Leftrightarrow4x^2+4x+1-\left(4x^2-9\right)=10\)
\(\Leftrightarrow4x=0\Rightarrow x=0\)

e) \(a^2+2ab+b^2-ac-bc=\left(a+b\right)^2-c\left(a+b\right)=\left(a+b-c\right)\left(a+b\right)\)
f) \(x^2-2x-4y^2-4y=x^2-2x+1-\left(4y^2+4y+1\right)=\left(x-1\right)^2-\left(2y+1\right)^2\)
\(=\left(x-2y-2\right)\left(x+2y\right)\)
g) \(x^2y-x^3-9y+9x=x^2\left(y-x\right)-9\left(y-x\right)=\left(x^2-9\right)\left(y-x\right)=\left(x-3\right)\left(x+3\right)\left(y-x\right)\)
h) \(x^2\left(x-1\right)+16\left(1-x\right)=\left(x^2-16\right)\left(x-1\right)=\left(x-4\right)\left(x+4\right)\left(x-1\right)\)

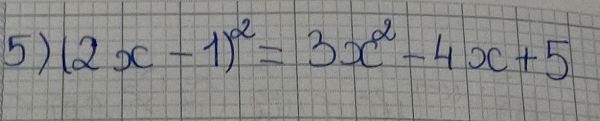
 nhớ cho mik nha =)
nhớ cho mik nha =)
Ta có: B = (2 +1)(22 +1)(24 +1)(28 +1)
= (22 - 1)(22 +1)(24 +1)(28 +1)
= (24 - 1)(24 +1)(28 +1)
= (28 - 1)(28 +1)
= 216 - 1
\(\Rightarrow\)B = 216 - 1 \(< \)216 = A