 giúp tớ với các cậu ơi
giúp tớ với các cậu ơi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
A : 3 dư 2
⇒ (A + 1) ⋮ 3
Mà 15 ⋮ 3 ⇒ (A + 1 + 15) ⋮ 3 ⇒ (A + 16) ⋮ 3
A : 7 dư 5
⇒ (A + 2) ⋮ 7
Mà 14 ⋮ 7 ⇒ (A + 2 + 14) ⋮ 7 ⇒ (A + 16) ⋮ 7
Do 3 và 7 đều chỉ cùng ⋮ 1 ⇒ (A + 16) ⋮ (3 x 7)
⇒ (A + 16) ⋮ 21
Mà 21 ⋮ 21 ⇒ (A + 16 - 21) ⋮ 21 ⇒ (A - 5) ⋮ 21
Vậy A : 21 → dư 5
Đáp số: 5

Chu vi của phần giảm đi là:
\(160-120=40\left(cm\right)\)
Vì hình chữ nhật đã bị giảm chiều dài và rộng cùng một độ dài nên phần giảm đi là 1 hình vuông
Độ dài cạnh của phần giảm đi là:
\(40:4=10\left(cm\right)\)
Diện tích phần giảm đi là:
\(10\times10=100\left(cm^2\right)\)

Ctv vip là một cộng tác viên vip của Olm so với ctv thì ctv vip có thể tick ra gp em nhé.

Thông thường thì hai nghiệm phải có quan hệ với nhau, sao biểu thức trong căn chỉ chứa \(x_1\) vậy em?

Lời giải:
$\Delta' (*) = 4^2-8(m^2+1)=8-8m^2$
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'(*) = 8-8m^2\geq 0\Leftrightarrow 1-m^2\geq 0$
$\Leftrightarrow -1\leq m\leq 1$
Áp dụng định lý Viet:
$x_1+x_2=1$
$x_1x_2=\frac{m^2+1}{8}$
Khi đó:
$x_1^4-x_2^4=x_1^3-x_2^3$
$\Leftrightarrow (x_1^2-x_2^2)(x_1^2+x_2^2)=(x_1-x_2)(x_1^2+x_1x_2+x_2^2)$
$\Leftrightarrow (x_1-x_2)[(x_1+x_2)(x_1^2+x_2^2)-(x_1^2+x_1x_2+x_2^2)]=0$
$\Leftrightarrow (x_1-x_2)[1(x_1^2+x_2^2)-(x_1^2+x_1x_2+x_2^2)]=0$
$\Leftrightarrow (x_1-x_2)(-x_1x_2)=0$
$\Leftrightarrow (x_1-x_2).\frac{-(m^2+1)}{8}=0$
$\Leftrightarrow x_1-x_2=0$ (do $m^2+1\geq 1>0$ với mọi $m$ nên số này khác 0)
$\Leftrightarrow x_1=x_2$
Kết hợp $x_1+x_2=1$
$\Rightarrow x_1=x_2=\frac{1}{2}$
$\frac{m^2+1}{8}=x_1x_2=\frac{1}{4}$
$\Leftrightarrow m^2+1=2$
$\Leftrightarrow m^2=1\Leftrightarrow m=\pm 1$ (tm)

3,24 x \(x\) - 2,4 x 0,38 = 21,12
3,24 x \(x\) - 0,912 = 21,12
3,24 x \(x\) = 21,12 + 0,912
3,24 x \(x\) = 22,032
\(x\) = 22,032 : 3,24
\(x\) = 6,8
3,24 x X - 2,4 x 0,38 = 21,12
3,24 x X - 0,912 = 21,12
3,24 x X = 21,12 + 0,912
3,24 x X = 22,032
X = 22,032 : 3,24
X = 6,8

Lời giải:
$BC=\sqrt{AB^2+AC^2}=\sqrt{18^2+24^2}=30$ (cm) - áp dụng định lý Pitago.
Nửa chu vi tam giác: $p=(AB+BC+AC):2=(18+24+30):2=36$ (cm)
Diện tích: $S=AB.AC:2=18.24:2=216$ (cm2)
Áp dụng công thức:
$S=pr$ với $r$ là bán kính đường tròn nội tiếp tam giác.
$r=\frac{S}{p}=\frac{216}{36}=6$ (cm)

Lời giải:
$A=\frac{(2011\times 2022+2011)+2023\times 11}{2022\times (2021-2020)}$
$=\frac{2011\times(2022+1)+2023\times 11}{2022\times 1}$
$=\frac{2011\times 2023+2023\times 11}{2022}$
$=\frac{2023\times (2011+11)}{2022}=\frac{2023\times 2022}{2022}=2023$
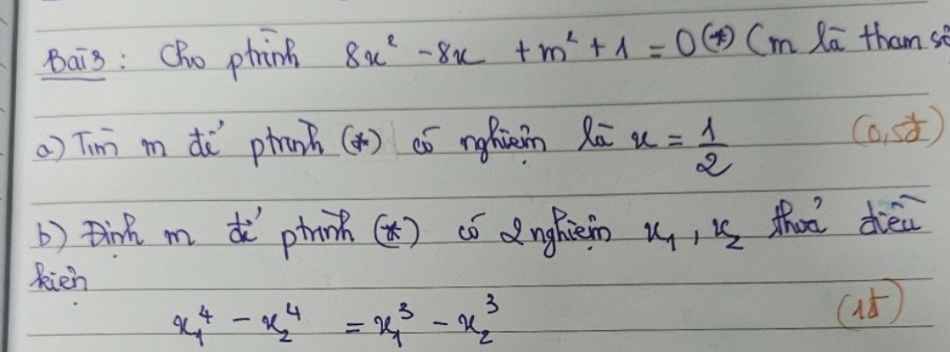

Câu 26:
a: Vì D là trung điểm của BC
nên \(S_{ADB}=S_{ADC}=\dfrac{S_{ABC}}{2}\)
Vì \(AM=\dfrac{1}{3}AC\)
nên \(S_{AMD}=\dfrac{1}{3}\times S_{ADC}=\dfrac{1}{3}\times\dfrac{1}{2}\times S_{ABC}=\dfrac{1}{6}\times S_{ABC}\)
b: Vì \(AM=\dfrac{1}{3}AC\)
nên \(S_{ABM}=\dfrac{1}{3}\times S_{ABC}\)
Vì AN=NB
nên N là trung điểm của AB
=>\(AN=\dfrac{1}{2}AB=NB\)
\(AN=\dfrac{1}{2}AB\)
=>\(S_{ANM}=\dfrac{1}{2}\times S_{ABM}=\dfrac{1}{6}\times S_{ABC}\)
Vì \(BM=\dfrac{1}{2}AB\)
nên \(S_{BND}=\dfrac{1}{2}\times S_{ABD}=\dfrac{1}{4}\times S_{ABC}\)
Vì \(AM=\dfrac{1}{3}AC\)
nên \(CM=\dfrac{2}{3}AC\)
=>\(S_{DMC}=\dfrac{2}{3}\times S_{ADC}=\dfrac{1}{3}\times S_{ABC}\)
Ta có: \(S_{ANM}+S_{DNM}+S_{BND}+S_{MDC}=S_{ABC}\)
=>\(S_{DNM}+\dfrac{1}{3}\times S_{ABC}+\dfrac{1}{4}\times S_{ABC}+\dfrac{1}{6}\times S_{ABC}=S_{ABC}\)
=>\(S_{DNM}=\dfrac{1}{4}\times S_{ABC}=150\left(cm^2\right)\)
Câu 25:
Tỉ số giữa số bi xanh và số bi đỏ là:
\(\dfrac{1}{8}:\dfrac{1}{9}=\dfrac{9}{8}\)
Số bi xanh là: 170:17x9=90(viên)
Số bi đỏ là 170-90=80(viên)