ΔAEH vuông tại E

mà EI là đường trung tuyến

nên IE=IH

=>ΔIEH cân tại I

ΔBEC vuông tại E

mà EK là đường trung tuyến

nên KE=KB

=>ΔKEB cân tại K

\(\widehat{IEK}=\widehat{IEB}+\widehat{KEB}=\widehat{IHE}+\widehat{KBE}\)

\(=\widehat{BHD}+\widehat{DBH}=90^0\)

=>IE\(\perp\)EK

\(-\dfrac{3}{11}.\dfrac{5}{7}+\dfrac{5}{7}.-\dfrac{8}{11}+\dfrac{19}{7}\)

`=` \(\dfrac{5}{7}.\left(\dfrac{-3}{11}+\dfrac{-8}{11}\right)+\dfrac{19}{7}\)

`=` \(\dfrac{5}{7}.\dfrac{-11}{11}+\dfrac{19}{7}\)

`=` \(\dfrac{5}{7}.\left(-1\right)+\dfrac{19}{7}\)

`=` \(-\dfrac{5}{7}+\dfrac{19}{7}\)

`=` \(\dfrac{14}{7}\)

`=  2`

(-\(\dfrac{1}{2}\))³:(-\(\dfrac{1}{2}\))⁶=(-\(\dfrac{1}{8}\)):\(\dfrac{1}{64}\)=-\(\dfrac{64}{8}\)=-8

`#3107.101107`

\(\left(-\dfrac{1}{2}\right)^3\div\left(-\dfrac{1}{2}\right)^6\\ =\left(-\dfrac{1}{2}\right)^{3-6}\\ =\left(-\dfrac{1}{2}\right)^{-3}\\ =\left(-2\right)^3\\ =-8\)

`2^x + 2^y = 192`

Ta có: `2^7 = 128 < 192 ; 2^8 = 256 > 192`

Nên `x;y < 8`

Không mất tính tổng quát, xét: 

`-> x = 1` thì `y` không phải là số tự nhiên

`-> x = 2` thì `y` không phải là số tự nhiên

`-> x = 3` thì `y` không phải là số tự nhiên

`-> x = 4` thì `y` không phải là số tự nhiên

`-> x = 5` thì `y` không là số tự nhiên

`-> x = 6` thì `y` không phải là số tự nhiên

`-> x = 7` thì `y = 6` (Thỏa mãn)

Vậy ` (x;y) = (7;6); (6;7)`

\(14-8x^2=\dfrac{3}{2}\\ =>8x^2=14-\dfrac{3}{2}\\ =>8x^2=\dfrac{25}{2}\\ =>x^2=\dfrac{25}{2}:8\\ =>x^2=\dfrac{25}{16}\\ =>x=\pm\dfrac{5}{4}\)

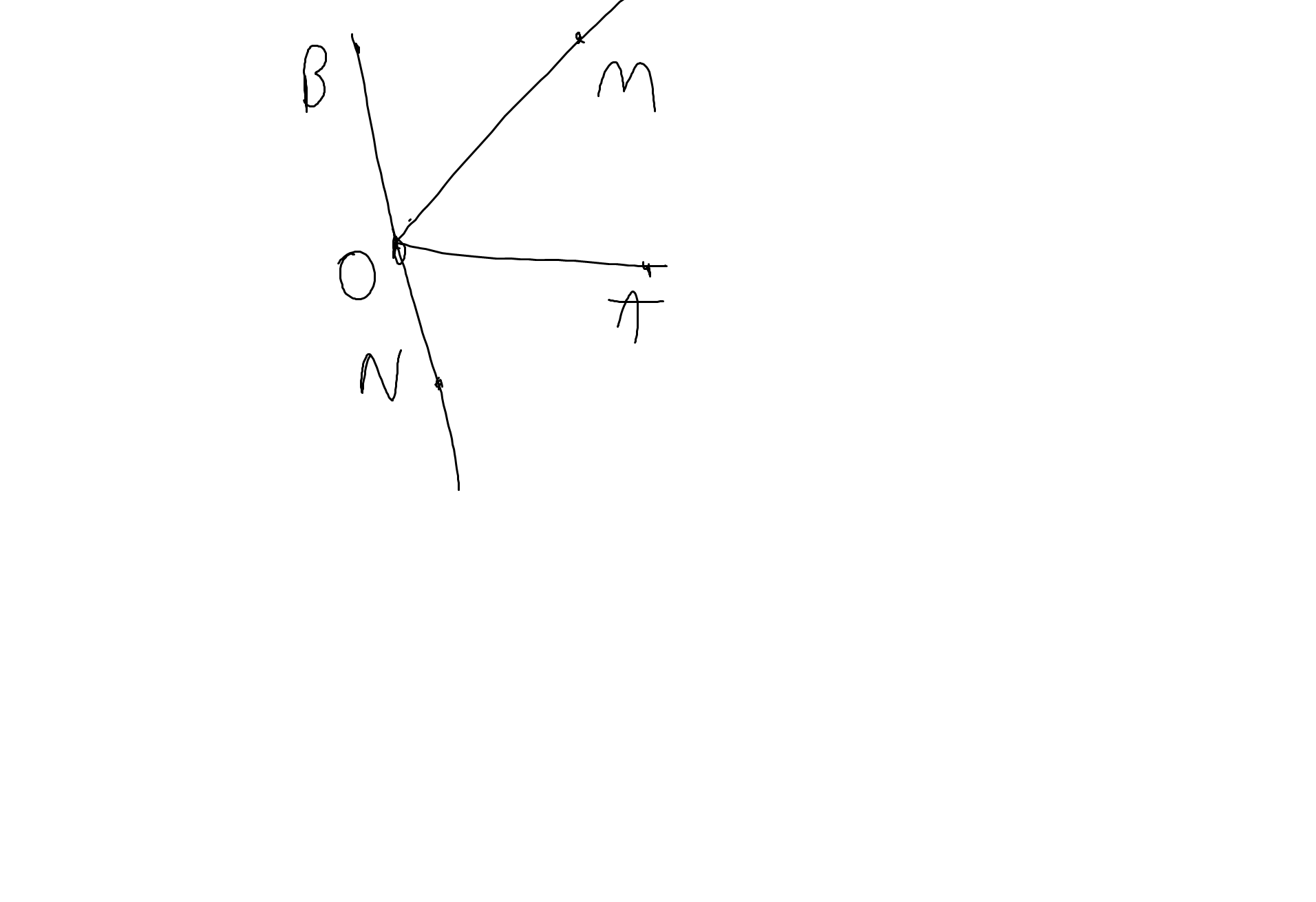
a: Ta có: \(\widehat{A'OC}+\widehat{AOC}=180^0\)(kề bù)

=>\(\widehat{AOC}+90^0=180^0\)

=>\(\widehat{AOC}=90^0\)

Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\widehat{AOB}< \widehat{AOC}\)

nên tia OB nằm giữa hai tia OA và OC

=>\(\widehat{AOB}+\widehat{BOC}=\widehat{AOC}\)

=>\(\widehat{BOC}=90^0-45^0=45^0\)

Ta có: \(\widehat{AOB}=\widehat{BOC}\)

mà tia OB nằm giữa hai tia OA và OC

nên OB là phân giác của góc AOC

b: Ta có: \(\widehat{COB}+\widehat{COE}=180^0\)(hai góc kề bù)

=>\(\widehat{COE}+45^0=180^0\)

=>\(\widehat{COE}=135^0\)

Bài 1:

a: OM là phân giác của góc AOB

=>\(\widehat{AOM}=\dfrac{\widehat{AOB}}{2}=\dfrac{120^0}{2}=60^0\)

b: Vì OM và OM là hai tia trùng nhau

nên \(\widehat{MOM}=0^0\)

\(a.\left(4x+1\right)\left(-2x+\dfrac{1}{3}\right)=0\\ TH1:4x+1=0\\ =>4x=-1\\ =>x=-\dfrac{1}{4}\\ TH2:-2x+\dfrac{1}{3}=0\\ =>2x=\dfrac{1}{3}\\ =>x=\dfrac{1}{3}:2=\dfrac{1}{6}\\ b.\left(x-\dfrac{5}{2}\right)^3=\dfrac{-1}{8}\\ =>\left(x-\dfrac{5}{2}\right)^3=\left(-\dfrac{1}{2}\right)^2\\ =>x-\dfrac{5}{2}=-\dfrac{1}{2}\\ =>x=-\dfrac{1}{2}+\dfrac{5}{2}\\ =>x=\dfrac{4}{2}=2\\ c.\left(\dfrac{2}{5}-3x\right)^2-\dfrac{1}{5}=\dfrac{4}{25}\\ =>\left(\dfrac{2}{5}-3x\right)^2=\dfrac{4}{25}+\dfrac{1}{5}=\dfrac{9}{25}=\left(\dfrac{3}{5}\right)^2\\TH1:\dfrac{2}{5}-3x=\dfrac{3}{5}\\ =>3x=\dfrac{2}{5}-\dfrac{3}{5}=-\dfrac{1}{5}\\ =>x=\dfrac{-1}{5}:3=-\dfrac{1}{15}\\ TH2:\dfrac{2}{5}-3x=-\dfrac{3}{5}=>3x=\dfrac{2}{5}+\dfrac{3}{5}=1\\ =>x=1:3=\dfrac{1}{3}\) 

\(d.\left(\dfrac{2}{3}\right)^{x+2}+\left(\dfrac{2}{3}\right)^{x+1}=\dfrac{20}{27}\\ =>\left(\dfrac{2}{3}\right)^{x+1}\cdot\left(\dfrac{2}{3}+1\right)=\dfrac{20}{27}\\ =>\left(\dfrac{2}{3}\right)^{x+1}\cdot\dfrac{5}{3}=\dfrac{20}{27}\\ =>\left(\dfrac{2}{3}\right)^{x+1}=\dfrac{20}{27}:\dfrac{5}{3}=\dfrac{4}{9}=\left(\dfrac{2}{3}\right)^2\\ =>x+1=2\\ =>x=2-1\\ =>x=1\)

Số đối của 5/6 là -5/6

Số đối của \(-\dfrac{5}{2}\) là \(\dfrac{5}{2}\)

Số đối của 0,8 là -0,8

Biểu diễn:

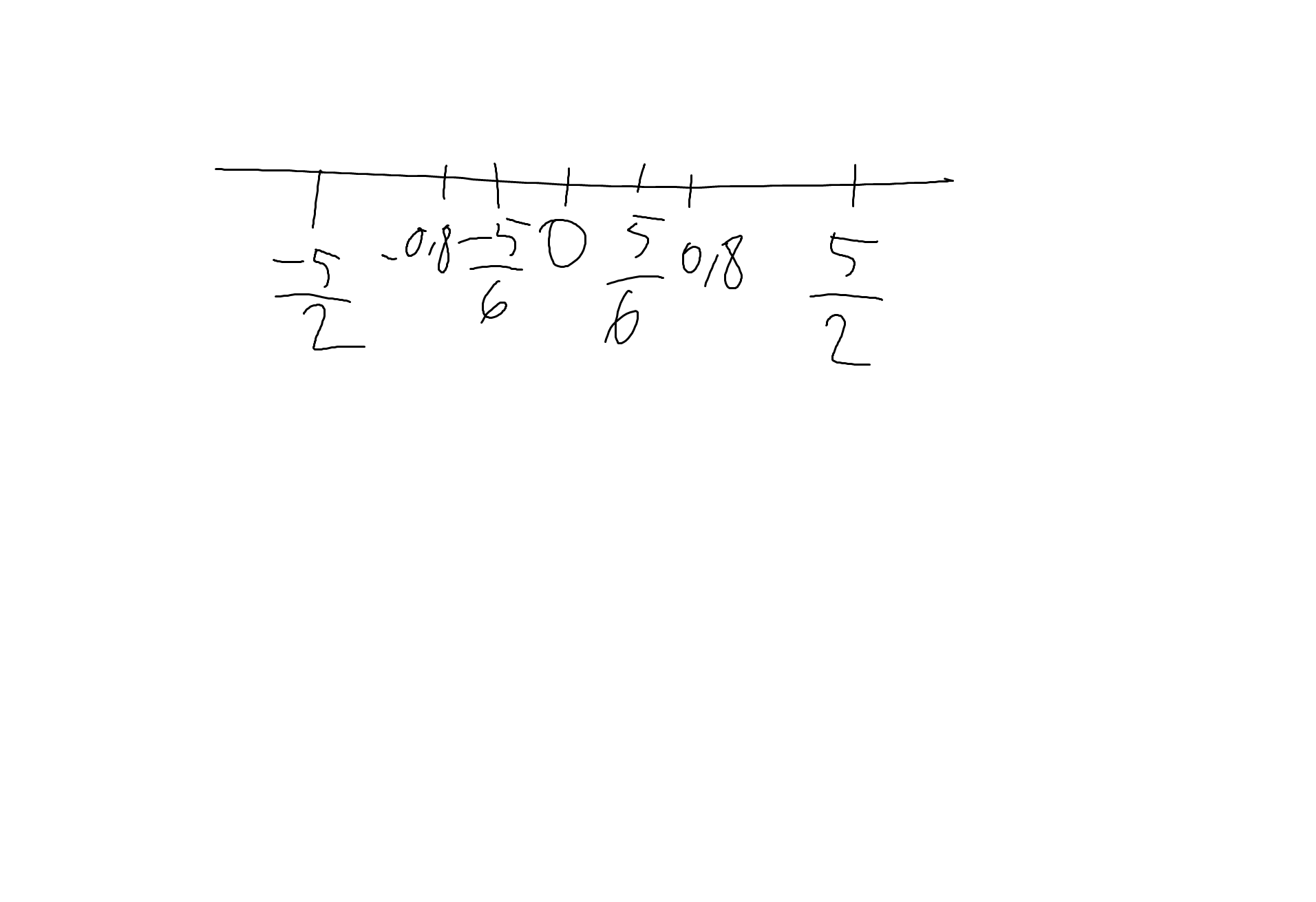
\(x\left(2x+\dfrac{-4}{10}\right)\) = 0

\(\left[{}\begin{matrix}x=0\\2x-\dfrac{4}{10}=10\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=0\\2x=\dfrac{4}{10}\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=0\\x=\dfrac{4}{10}:2\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=0\\x=\dfrac{1}{5}\end{matrix}\right.\)

Vậy \(x\) \(\in\) {0; \(\dfrac{1}{5}\)}

\(x\left(2x+\dfrac{-4}{10}\right)=0\\ =>x\left(2x+\dfrac{-2}{5}\right)=0\\ =>2x\left(x-\dfrac{1}{5}\right)=0\\ TH1:2x=0\\ =>x=0\\ TH2:x-\dfrac{1}{5}=0\\ =>x=\dfrac{1}{5}\)