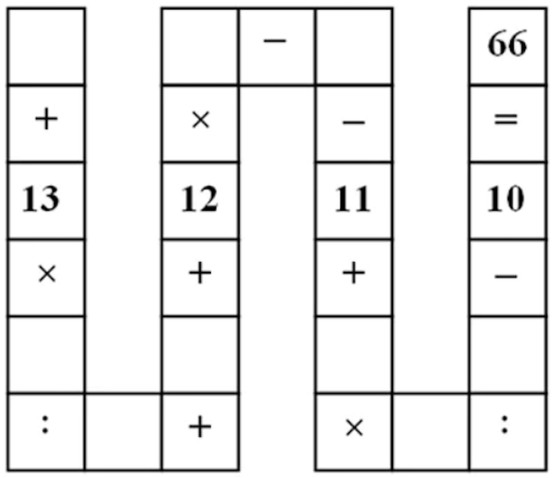
Điền các số từ 1 - 9 (không trùng lặp) vào ô trống trên bảng tính hình rắn phía trên.
SOS giúp mik vs! Mik cần gấp. Cảm ơn ! Mik đăng lần này là lân thứ ba rùi mong mọi người giúp mik.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi K' là giao điểm của BI và EF, S là giao điểm của EJ và AB.
Ta có \(\left(FSBA\right)=-1\) (hàng điều hòa quen thuộc). Mặt khác, dễ thấy K'B là trung trực của FJ nên K'B cũng là tia phân giác của \(\widehat{FK'S}\)
Do đó, \(\widehat{AK'B}=90^o\). Khi đó tam giác AK'B vuông tại K' có trung tuyến K'M nên \(K'M=MB=\dfrac{1}{2}AB\)
Từ đó suy ra tam giác MK'B cân tại M \(\Rightarrow\widehat{MK'B}=\widehat{MBK'}=\widehat{K'BC}\)
Do đó MK'//BC. Chú ý rằng MN là đường trung bình của tam giác ABC \(\Rightarrow\) MN//BC. Vậy \(K'\in MN\) hay K' chính là giao điểm của MN và JE. Điều này có nghĩa là \(K'\equiv K\).
Như vậy, \(K,B,I\) thẳng hàng và \(\widehat{AKB}=90^o\) hay \(AK\perp BI\)
Lại có \(FJ\perp BI\) nên AK//FJ hay AK//HJ.
Tương tự, ta cũng có AH//KJ nên tứ giác AKJH là hình bình hành.
\(\Rightarrow\) HK, AJ cắt nhau tại trung điểm mỗi đoạn, hay JA đi qua trung điểm của HK.
câu a ý 2:
Gọi U là giao điểm của EF và BC, P là trung điểm BC, X là điểm chính giữa cung BC không chứa D của (O).
Có \(\widehat{XIB}=\widehat{IAB}+\widehat{IBA}=\widehat{XCB}+\widehat{IBC}=\widehat{XBC}+\widehat{IBC}=\widehat{XBI}\) nên tam giác XBI cân tại X \(\Rightarrow XB=XI\)
Tương tự, ta cũng có \(XB=XC=XI\) nên X là tâm (IBC)
Dễ thấy \(\widehat{XBD}=\widehat{XCD}=90^o\) nên XB, XC là tiếp tuyến tại B và C của (X).
\(\Rightarrow DC^2=DP.DX=DT.DG\) \(\Rightarrow\) Tứ giác TPXG nội tiếp.
\(\Rightarrow\widehat{DPT}=\widehat{XGT}=\widehat{XTG}=\widehat{XPG}\)
\(\Rightarrow90^o-\widehat{DPT}=90^o-\widehat{XPG}\)
\(\Rightarrow\widehat{UPT}=\widehat{UPG}\) . Do \(\widehat{UPG}+\widehat{GPC}=180^o\)
\(\Rightarrow\) \(\widehat{GPC}+\widehat{UPT}=180^o\)
Vì D là giao điểm của 2 tiếp tuyến tại B và C của đường tròn (X) nên GD là đối trung của tam giác GBC
\(\Rightarrow\widehat{BGT}=\widehat{PGC}\)
Lại có \(\widehat{GTB}=\widehat{GCP}\) \(\Rightarrow\Delta GTB\sim\Delta GCP\) \(\Rightarrow\widehat{GBT}=\widehat{GPC}\)
Lại có \(\widehat{GBT}=\widehat{GIT}\) nên \(\widehat{GPC}=\widehat{GIT}\)
Kết hợp với \(\widehat{GPC}+\widehat{UPT}=180^o\), ta có \(\widehat{GIT}+\widehat{UPT}=180^o\)
\(\Rightarrow\) Tứ giác ITPJ nội tiếp.
Mặt khác, \(\left(BCJU\right)=-1\) và P là trung điểm BC nên \(\overline{UJ}.\overline{UP}=\overline{UB}.\overline{UC}\) (hệ thức Maclaurin)
\(\Rightarrow P_{U/\left(ITPJ\right)}=P_{U/\left(X\right)}\)
\(\Rightarrow\) U nằm trên trục đẳng phương của đường tròn (ITPJ) và (X), mà IT là trục đẳng phương của 2 đường tròn này nên U, I, T thẳng hàng.
Xét cực và đối cực đối với (I). Kí hiệu \(d_Y\) là đối cực của Y đối với (I).
Ta có \(\left(BCJU\right)=-1\) \(\Rightarrow J\in d_U\)
Lại có \(U\in EF\equiv d_A\Rightarrow A\in d_U\)
Do đó \(JA\equiv d_U\) \(\Rightarrow JA\perp UI\) hay \(JA\perp IT\) (đpcm)

Đặt \(f\left(x\right)=y=\dfrac{1}{3}x^3-\left(2m-1\right)x^2+\left(m^2-m+7\right)x+m-5\)
=>\(y'=\dfrac{1}{3}\cdot3x^2-\left(2m-1\right)\cdot2x^2+\left(m^2-m+7\right)\)
=>\(y'=x^2-\left(4m-2\right)x^2+\left(m^2-m+7\right)\)
Đặt y'=0
\(\text{Δ}=\left(4m-2\right)^2-4\left(m^2-m+7\right)\)
\(=16m^2-16m+4-4m^2+4m-28=12m^2-12m-24\)
Để hàm số f(x) có hai cực trị thì Δ>0
=>\(12\left(m^2-m-2\right)>0\)
=>\(m^2-m-2>0\)
=>(m-2)(m+1)>0
=>\(\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4m-2\\x_1x_2=\dfrac{c}{a}=m^2-m+7\end{matrix}\right.\)
\(x_1^2+x_2^2=\left(\sqrt{74}\right)^2=74\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2=74\)
=>\(\left(4m-2\right)^2-2\left(m^2-m+7\right)=74\)
=>\(16m^2-16m+4-2m^2+2m-14=74\)
=>\(14m^2-14m-84=0\)
=>\(m^2-m-6=0\)
=>(m-3)(m+2)=0
=>\(\left[{}\begin{matrix}m=3\left(nhận\right)\\m=-2\left(nhận\right)\end{matrix}\right.\)

\(y'=3x^2+1\)
Do 3x^2 >= 0 => 3x^2 + 1 > 0
=> hs đồng biến trên R

Xet tam giac ABC co
\(cos60=\dfrac{AB^2+AC^2-BC^2}{2.AB.AC}\Rightarrow BC=\sqrt{3}a\)
\(cosACB=\dfrac{AC^2+BC^2-AB^2}{2.AC.BC}\Rightarrow\widehat{ACB}=30^0\)
Cho H la giao diem giua AG va BC => HC = can3/2
Xet tam giac AHC
\(cosACB=\dfrac{AC^2+CH^2-AH^2}{2.AC.CH}\Rightarrow AH=\dfrac{\sqrt{7}a}{2}\)
\(\Rightarrow AG=\dfrac{2}{3}.\dfrac{\sqrt{7}a}{2}=\dfrac{\sqrt{7}a}{3}\)
Ma (AA';A'G) = ^AA'G = 300
Xet tam giac A'AG vuong tai G
tanAA'G = \(\dfrac{AG}{A'G}=\dfrac{\sqrt{7}a}{3}:A'G=\dfrac{\sqrt{3}}{3}\Rightarrow A'G=\dfrac{\sqrt{21}a}{3}\)
Xet tam giac ABC
SABC = \(\dfrac{1}{2}.a.2a.sin60^0=\dfrac{\sqrt{3}}{2}a^2\)
\(V_{ABC.A'B'C}=A'G.S_{ABC}=\dfrac{\sqrt{21}}{3}a.\dfrac{\sqrt{3}}{2}a^2=\dfrac{\sqrt{7}}{2}a^3\)

Chọn hệ trục tọa độ Mxyz (M là gốc tọa độ) sao cho Mx trùng với tia MB, My trùng với tia MA và Mz cùng phương với BB' sao cho \(\overrightarrow{BB'}\) hướng theo chiều dương của Mz.
Gọi chiều cao lăng trụ là \(h>0\)
Khi đó \(B\left(a;0;0\right)\), \(C'\left(-a;0;h\right)\), \(A'\left(0;a\sqrt{3};h\right)\)
Ta có \(\overrightarrow{MC'}=\left(-a;0;h\right),\overrightarrow{BA'}=\left(-a;a\sqrt{3};h\right)\)
\(\Rightarrow\left[\overrightarrow{MC'},\overrightarrow{BA'}\right]=\left(-ah\sqrt{3};0;a^2\sqrt{3}\right)\)
\(\Rightarrow\left|\left[\overrightarrow{MC'},\overrightarrow{BA'}\right]\right|=\sqrt{\left(-ah\sqrt{3}\right)^2+\left(a^2\sqrt{3}\right)^2}=a\sqrt{3h^2+3a^2}\)
Lại có \(\overrightarrow{MB}=\left(a;0;0\right)\)
\(\Rightarrow\left[\overrightarrow{MC'},\overrightarrow{BA'}\right].\overrightarrow{MB}=-a^2h\sqrt{3}\)
\(\Rightarrow d\left(MC',BA'\right)=\dfrac{\left|\left[\overrightarrow{MC'},\overrightarrow{BA'}\right].\overrightarrow{MB}\right|}{\left|\left[\overrightarrow{MC'},\overrightarrow{BA'}\right]\right|}\) \(=\dfrac{a^2h\sqrt{3}}{a\sqrt{3a^2+3h^2}}=\dfrac{ah}{\sqrt{a^2+h^2}}\)
Theo đề bài, ta có: \(\dfrac{ah}{\sqrt{a^2+h^2}}=\dfrac{a}{2}\)
\(\Leftrightarrow\dfrac{h}{\sqrt{a^2+h^2}}=\dfrac{1}{2}\)
\(\Leftrightarrow2h=\sqrt{a^2+h^2}\)
\(\Leftrightarrow4h^2=a^2+h^2\)
\(\Leftrightarrow3h^2=a^2\)
\(\Leftrightarrow h=\dfrac{a}{\sqrt{3}}\)
\(\Rightarrow V=S_đ.h=\dfrac{\left(2a\right)^2\sqrt{3}}{4}.\dfrac{a}{\sqrt{3}}=a^3\)
Vậy thể tích lăng trụ bằng \(a^3\)

Đặt: \(\left\{{}\begin{matrix}z=a+bi\\w=c+di\\u=x+yi\end{matrix}\right.\)
\(\left|z-w\right|^2=\left|z\right|^2-2wz+\left|w\right|^2=50-2wz\) \(=50-2ac+2bd-2\left(ad+bc\right)i\) \(\left(1\right)\)
\(8\left|2u-z+w\right|=8\left|2x+2yi-a-bi+c+di\right|=8\sqrt{\left(2x-a+c\right)^2+\left(2y-b+d\right)^2}\)\(=8\sqrt{a^2-2ac-4ax+b^2-2bd-4yb+c^2+4cx+d^2+4dy+4x^2+4y^2}\) \(\left(2\right)\)
\(\left(z-4i\right)\left(\overline{w}-4i\right)=ac-\left(b-4\right)^2+ac\left(d-4\right)i\) biết \(\left\{{}\begin{matrix}ac-\left(b-4\right)^2>0\\ac\left(d-4\right)=0\rightarrow d=4\end{matrix}\right.\)
\(\left(2u+z-w-8i\right)\left(\overline{z-w-2u}\right)=\left(2x+2yi+a+bi-c-di-8i\right)\)\(\left(\overline{a+bi-c-di-2x+2yi}\right)\) \(=a^2-2ac+c^2-4x^2\)\(+(ab+ad-cb-cd-2ya\) \(-2yc+2xb+2xd-4xy)i\) \(+(2ay+ab-ad-8a\) \(-2cy-cb+cd+8c\) \(-4xy-2xb+2xd+16x)i\) \(+2yb-2yd+2y^2+b^2\) \(-bd+2yb-db+d^2+2yd\) \(-8b+8d-16y\) biết phần thực: \(a^2+b^2+c^2+d^2-2ac-2bd-4x^2\)\(+2y^2-8b+8a-16y>0\) và phần ảo: \(2ab-2cb+4cy+4xd\) \(+8xy+8c-8a+16x=0\)
Rút gọn $P$ ta được: \(P=\sqrt{x^2-y^2-4x+5+2i\left(xy-2y\right)}\) \(+\sqrt{2\left(-2x^2+2y^2-6y-2x+4-\left(4xy-2y+3\right)i\right)}\)
\(\rightarrow\) Lú quá đi ngủ!