Lời giải:
Ta có:
$\frac{1}{x}-\frac{1}{y}=\frac{y-x}{xy}=\frac{-(x-y)}{xy}=\frac{-xy}{xy}=-1$

Gọi 120 số 1 hoặc -1 đó lần lượt là a₁; a₂; a₃; ...; a₁₂₀. Theo đề ta có:

a₁.a₂.a₃ = -1; a₂.a₃.a₄ = -1; a₃.a₄.a₅ = -1; ...;

a₁₁₈.a₁₁₉.a₁₂₀ = -1; a₁₁₉.a₁₂₀.a₁ = -1; a₁₂₀.a₁.a₂ = -1.

\(a_1=a_4=\dfrac{1}{a_2\cdot a_3}\); \(a_2=a_5=\dfrac{1}{a_3\cdot a_4}\); \(a_3=a_6=\dfrac{1}{a_4\cdot a_5}\); ...;

\(a_{118}=a_1=\dfrac{1}{a_{119}\cdot a_{120}}\); \(a_{119}=a_2=\dfrac{1}{a_{120}\cdot a_1}\); \(a_{120}=a_3=\dfrac{1}{a_1\cdot a_2}\).

Từ đây ta suy ra \(a_1=a_4=a_7=...=a_{118}\); \(a_2=a_5=a_8=...=a_{119}\); \(a_3=a_6=a_9=...=a_{120}\). (1)

Do đó \(a_1=\dfrac{1}{a_2\cdot a_3}\); \(a_2=\dfrac{1}{a_3\cdot a_1}\); \(a_3=\dfrac{1}{a_1\cdot a_2}\). Mà a₁.a₂.a₃ = -1 và các số a₁; a₂; a₃; ...; a₁₂₀ chỉ có thể là 1 hoặc -1 nên chỉ có một nghiệm duy nhất \(a_1=a_2=a_3=-1\). (2)

Từ (1) và (2) suy ra có 120 số -1, nên tổng của 120 số đó là \(120\cdot\left(-1\right)=-120\).

a) \(\dfrac{35}{101}=\dfrac{105}{303}< \dfrac{189}{303}\Rightarrow\dfrac{35}{101}< \dfrac{189}{303}\)

b) \(\dfrac{11}{13}< \dfrac{11+2}{13+2}=\dfrac{13}{15}< \dfrac{14}{15}\Rightarrow\dfrac{11}{-13}>\dfrac{-14}{15}\)

c) \(-\dfrac{32}{19}< 0< \dfrac{23}{32}\Rightarrow-\dfrac{32}{19}< \dfrac{23}{32}\)

d) \(1,561< 1,5661\Rightarrow-1,561>-1,5661\)

e) \(0,1=\dfrac{1}{10}=\dfrac{40}{400}< \dfrac{40+56}{400+56}=\dfrac{96}{456}< \dfrac{176}{456}\Rightarrow0,1< \dfrac{176}{456}\)

g) \(0,3=\dfrac{3}{10}=\dfrac{9}{30}< \dfrac{9+8}{30+8}=\dfrac{17}{38}< \dfrac{19}{38}\Rightarrow0,3< \dfrac{19}{38}\Rightarrow-0,3>\dfrac{-19}{38}\)

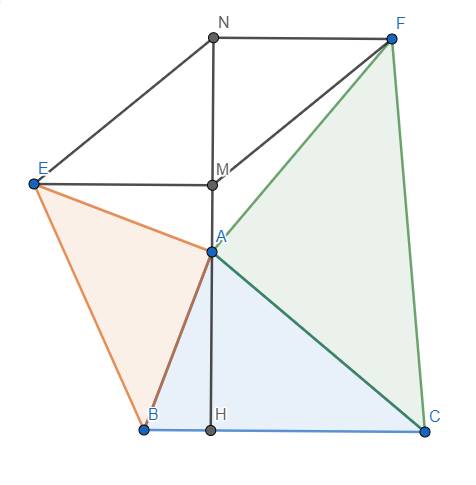
a) Do tam giác AEB vuông cân tại A nên \(\left\{{}\begin{matrix}\widehat{EAB}=90^o\\AE=AB\end{matrix}\right.\)

Ta thấy \(\widehat{MEA}=\widehat{BAH}\) vì chúng cùng phụ với \(\widehat{EAM}\)

Xét 2 tam giác HAB vuông tại H và MEA vuông tại M, ta có:

\(AE=AB\left(cmt\right),\widehat{MEA}=\widehat{BAH}\left(cmt\right)\)

\(\Rightarrow\Delta HAB=\Delta MEA\left(ch-gn\right)\) \(\Rightarrow AH=ME\)     (1)

Tương tự, ta cũng có \(\Delta HAC=\Delta NFA\Rightarrow HC=AN\)     (2)

Từ (1) và (2) suy ra \(EM+HC=AH+AN\) hay \(EM+HC=HN\) (đpcm)

b) Từ \(\Delta HAC=\Delta NFA\Rightarrow AH=NF\)

Từ đó suy ra \(ME=NF\left(=AH\right)\)

Xét tam giác MNE và NMF, ta có:

\(ME=NF\left(cmt\right),\widehat{EMN}=\widehat{FNM}\left(=90^o\right)\), MN là cạnh chung.

\(\Rightarrow\Delta MNE=\Delta NMF\left(c.g.c\right)\)

\(\Rightarrow\widehat{ENM}=\widehat{FMN}\) \(\Rightarrow\) EN//FM (2 góc so le trong bằng nhau)

Ta có đpcm.

mình đang cần gâps

625⁵ và 125⁷

a, 625⁵ = (5⁴)⁵ = 5²⁰

125⁷ = (5³)⁷ = 5²¹

Vì 5²⁰ < 5²¹ nên 625⁵ < 125⁷

b,  3²ⁿ = (3²)ⁿ = 9ⁿ

     2³ⁿ = (2³)ⁿ = 8ⁿ

     9ⁿ > 8ⁿ ( nếu n > 0)

      9ⁿ = 8ⁿ (nếu n = 0)

Vậy nếu n = 0 thì 2³ⁿ = 3²ⁿ
      nếu n > 0 thì 3²ⁿ > 2³ⁿ

Cảm ơn em đã báo cáo bài học. Cô đã duyệt toàn bộ nội dung bài giảng nhé. Bài giảng chuẩn và không có lỗi.

lỗi đâu mà lỗi 

có lẽ cậu học ko đc tốt(BPTT nói giảm nói tránh)hehe

bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb

Gọi `3` lớp `7A,7B,7C` trồng cây lần lượt là `a,b,c` \(\left(a,b,c\in N\right)\) 

Theo bài ra ta có : \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)  và `a+b+c=60` 

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{60}{12}=5\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{3}=5\Rightarrow a=5\cdot3=15\\\dfrac{b}{4}=5\Rightarrow b=5\cdot4=20\\\dfrac{c}{5}=5\Rightarrow c=5\cdot5=25\end{matrix}\right.\)

Vậy ...

Gọi \(x;y;z\left(x;y;z>0\right)\) lần lượt là số cây lớp 7A; 7B; 7C trồng

Theo đề bài ta có :

\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{3+4+5}=\dfrac{60}{12}=5\)

\(\Rightarrow\left\{{}\begin{matrix}x=3.5=15\\y=4.5=20\\z=5.5=25\end{matrix}\right.\)

Vậy lớp 7A trồng được : 15 cây

             7B trồng được : 20 cây

             7C trồng được : 25 cây

a) \(x=\dfrac{m-2023}{-2024}\)

Để \(x>0\)

\(\Leftrightarrow\dfrac{m-2023}{-2024}>0\)

\(\Leftrightarrow m-2023< 0\)

\(\Leftrightarrow m< 2023\)

b) Để \(x< 0\)

\(\Leftrightarrow\dfrac{m-2023}{-2024}< 0\)

\(\Leftrightarrow m-2023>0\)

\(\Leftrightarrow m>2023\)

c) Để \(x\) là số không dương cũng không âm

\(\Leftrightarrow\dfrac{m-2023}{-2024}=0\)

\(\Leftrightarrow m-2023=0\)

\(\Leftrightarrow m=2023\)

a) Để x là số dương khi:

\(m-2023< 0\)                     \(\left(-2024< 0\right)\)

\(m< 0+2023\)

\(=>m< 2023\)

b) Để x là số âm khi:

\(m-2023>0\)                  \(\left(-2024< 0\right)\)

\(=>m>2023\)

c) Để x không là số dương cũng không là số âm khi:

\(m-2023=0\)

\(=>m=2023\)