Lời giải

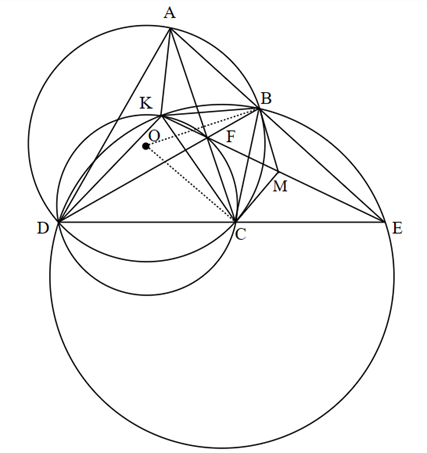
a) Vì điểm K nằm trên đường tròn ngoại tiếp ΔBDE nên tứ giác DKBE nội tiếp đường tròn

Suy ra $\widehat{BEK}=\widehat{BDK}$ (2 góc nội tiếp cùng chắn cung BK)

Hay $\widehat{AEK}=\widehat{FDK}$

Vì tứ giác DKFC nội tiếp đường tròn nên $\widehat{FCK}=\widehat{FDK}$

Suy ra $\widehat{AEK}=\widehat{FCK}$, hay $\widehat{AEK}=\widehat{ACK}$

Do đó tứ giác AKCE nội tiếp đường tròn

Suy ra $\widehat{KAE}+\widehat{KCE}={180}^{\circ }$

Mà $\widehat{KCD}+\widehat{KCE}={180}^{\circ }$ (hai góc kề bù)

Do đó $\widehat{KAE}=\widehat{KCD}$ hay $\widehat{KAB}=\widehat{KCD}$

Do tứ giác BKDE nội tiếp đường tròn nên $\widehat{KDE}+\widehat{KBE}={180}^{\circ }$

Mà $\widehat{KBA}+\widehat{KBE}={180}^{\circ }$ (hai góc kề bù)

Do đó $\widehat{KDE}=\widehat{KBA}$ hay $\widehat{KBA}=\widehat{KDC}$

Xét ΔDKC và ΔBKA có:

$\widehat{KBA}=\widehat{KDC}$ (chứng minh trên)

$\widehat{KAB}=\widehat{KCD}$ (chứng minh trên)

Suy ra (g.g)

Do đó $\frac{KC}{KA}=\frac{KD}{KB}$

Hay $\frac{KC}{KD}=\frac{KA}{KB}$

Ta có: $\widehat{BKD}=\widehat{DKC}+\widehat{BKC}$; $\widehat{AKC}=\widehat{BKA}+\widehat{BKC}$

Mà $\widehat{DKC}=\widehat{BKA}$, suy ra $\widehat{DKB}=\widehat{CKA}$

Xét ΔKBD và ΔKAC có:

$\widehat{DKB}=\widehat{CKA}$ (chứng minh trên)

$\frac{KC}{KD}=\frac{KA}{KB}$ (chứng minh trên)

Suy ra (c.g.c)

Do đó $\widehat{KBD}=\widehat{KAC}$

Hay $\widehat{KBF}=\widehat{KAF}$

Suy ra tứ giác AKFB nội tiếp đường tròn

Do đó $\widehat{BKF}=\widehat{BAF}$ (2 góc nội tiếp chắn cung BF)

Suy ra $\widehat{BKF}=\widehat{BAC}=\widehat{BDC}$ (do $\widehat{BAC},\widehat{BDC}$ cùng chắn cung BC)                   (1)

Ta có: $\widehat{BDC}=\widehat{FDC}=\widehat{FKC}$ (cùng chắn cung FC)                       (2)

Xét ΔBMC có $\widehat{MBC}+\widehat{MCB}+\widehat{BMC}={180}^{\circ }$ (tổng ba góc trong một tam giác)

Mà $\widehat{MBC}=\widehat{BAC},\widehat{MCB}=\widehat{BDC}$(Góc tạo bởi tiếp tuyến và dây cung)

Suy ra $\widehat{BAC}+\widehat{BDC}+\widehat{BMC}={180}^{\circ }$                                              (3)

Từ (1); (2) và (3) suy ra $\widehat{BKF}+\widehat{FKC}+\widehat{BMC}={180}^{\circ }$

Hay $\widehat{BKC}+\widehat{BMC}={180}^{\circ }$

Do đó tứ giác BKCM nội tiếp đường tròn

b) Ta có $\widehat{BKF}=\widehat{BDC}$ (chứng minh câu a)

Suy ra $\widehat{BKF}=\widehat{BDE}=\widehat{BKE}$ (Do tứ giác DKBE nội tiếp đường tròn)

Mà 2 điểm F và E nằm cùng phía so với BK

Suy ra 3 điểm K; F; E thẳng hàng

Hay F nằm trên KE                                                   (*)

Vì $\widehat{BKF}=\widehat{BAC},\widehat{CKF}=\widehat{BDC},\widehat{BAC}=\widehat{BDC}$

Nên $\widehat{BKF}=\widehat{CKF}$

Suy ra $\widehat{BKE}=\widehat{CKE}$ (Do K; F; E thẳng hàng)

Do đó KE là phân giác của $\widehat{BKC}$                     (4)

Xét (O) có MB, MC là 2 tiếp tuyến cắt nhau tại M

Nên MB = MC

Do đó tam giác MBC cân tại M

Suy ra $\widehat{MBC}=\widehat{MCB}$

Xét tứ giác BKCM nội tiếp đường tròn có $\widehat{MBC}=\widehat{MKC},\widehat{MCB}=\widehat{MKB}$

Suy ra $\widehat{MKC}=\widehat{MKB}$

Do đó KM là phân giác của $\widehat{BKC}$                                         (5)

Từ (4) và (5) suy ra 3 điểm K; M; E thẳng hàng hay M nằm trên KE (**)

Từ (*) và (**) suy ra 3 điểm E; M; F thẳng hàng

Vậy 3 điểm E; M; F thẳng hàng.

Gọi vận tốc dòng nước là a km/h ( a > 0 ) 

vận tốc xuôi dòng là a + 25 km/h 

vận tốc ngược dòng a - 25 km/h 

Ta có tổng thời gian đi lẫn về là 5h nên 

\(\dfrac{60}{a+25}+\dfrac{60}{a-25}=5\)

\(\Leftrightarrow60\left(a-25\right)+60\left(a+25\right)=5\left(a^2-25^2\right)\)

\(\Leftrightarrow120a=5a^2-5.25^2\Leftrightarrow\left[{}\begin{matrix}a=12+\sqrt{769}\\a=12-\sqrt{769}\left(l\right)\end{matrix}\right.\)

a = 25 thì pt vô nghiệm mà bạn?

ĐK: \(x\ge2,y\ge-2009,z\ge2010\)

Ta có: \(\sqrt{x-2}=\sqrt{1.\left(x-2\right)}\le\dfrac{1+x-2}{2}=\dfrac{x-1}{2}\)

\(\sqrt{y+2009}=\sqrt{1.\left(y+2009\right)}\le\dfrac{1+y+2009}{2}=\dfrac{y+2010}{2}\)

\(\sqrt{z-2010}=\sqrt{1.\left(z-2010\right)}\le\dfrac{1+z-2010}{2}=\dfrac{z-2009}{2}\)

Cộng theo vế 3 BĐT vừa tìm được, ta có:

\(VT=\sqrt{x-2}+\sqrt{y+2009}+\sqrt{z-2010}\)

\(\le\dfrac{x-1}{2}+\dfrac{y+2010}{2}+\dfrac{z-2009}{2}\)

\(=\dfrac{x-1+y+2010+z-2009}{2}\)

\(=\dfrac{1}{2}\left(x+y+z\right)\)

\(=VP\)

Do đó, dấu "=" phải xảy ra 

\(\Leftrightarrow x-2=y+2009=z-2010=1\)

\(\Leftrightarrow\left(x,y,z\right)=\left(3,-2008,2011\right)\)

Vậy pt đã cho có nghiệm duy nhất là \(\left(3,-2008,2011\right)\)

Nghiệm của x - 2 là 2 

A chia hết cho x - 2 nên ta thay nghiệm của x - 2 vào A ta có: 

\(A=a\cdot2^3+b\cdot2^2+2=0=>8a+4a+c=0\) (1) 

A(x) chia `x^2+x-2` dư 3x+2 nên A(x) - (3x+2) chia hết cho `x^2+x-2` 

Ta có nghiệm của là: \(x^2+x-2=0\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

Lần lượt thay `x=1` và `x=-2` vào A(x) - (3x+2) ta có: 

\(A=a\cdot1^3+b\cdot1^2+c-\left(3\cdot1+2\right)=0\Rightarrow a+b+c=5\) (2) 

\(A=a\cdot\left(-2\right)^3+b\cdot\left(-2\right)^2+c-\left(3\cdot-2+2\right)=0=>-8a+4b+c=-4\) (3) 

Từ (1) , (2) và (3) ta có hpt: \(\left\{{}\begin{matrix}8a+4b+c=0\\a+b+c=5\\-8a+4b+c=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{4}\\b=-\dfrac{9}{4}\\c=7\end{matrix}\right.\)

Để pt có nghiệm duy nhất thì: \(-\dfrac{2}{m}\ne\dfrac{1}{1}\Leftrightarrow m\ne-2\)

\(\left\{{}\begin{matrix}-2x+y=-3m-1\\mx+y=m^2+m+3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left(m+2\right)y=m^2+m+3+3m+1\\-2x+y=-3m-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{m^2+4m+4}{m+2}\\-2x+y=-3m-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{\left(m+2\right)^2}{m+2}=m+2\\-2x+\left(m+2\right)=-3m-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=m+2\\2x=m+2+3m+1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=m+2\\2x=4m+3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=m+2\\x=\dfrac{4m+2}{2}\end{matrix}\right.\) 

Mà: \(\left\{{}\begin{matrix}x>0\\y>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4m+2}{3}>0\\m+2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4m>-2\\m>-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{2}\\m>-2\end{matrix}\right.\Leftrightarrow m>-\dfrac{1}{2}\)

\(2x^4+ax^3+3x^2+4x+b⋮x^2-4x+4\)

=>\(2x^4-8x^3+8x^2+\left(a+8\right)x^3-\left(4a+32\right)x^2+\left(4a+32\right)x+\left(4a+27\right)x^2-4\cdot\left(4a+27\right)x+4\cdot\left(4a+27\right)+\left(12a+80\right)x+b-16a-108⋮x^2-4x+4\)

=>\(\left\{{}\begin{matrix}12a+80=0\\b-16a-108=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=-\dfrac{20}{3}\\b=16a+108=\dfrac{4}{3}\end{matrix}\right.\)