ghh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,dkxd:x\ne\dfrac{1}{3};x\ne-\dfrac{1}{3}\)
\(b,P=\left(\dfrac{3x}{1-3x}+\dfrac{2x}{3x+1}\right):\dfrac{6x^2+10x}{1-6x+9x^2}\)
\(=\dfrac{3x\left(3x+1\right)+2x\left(1-3x\right)}{\left(1-3x\right)\left(1+3x\right)}.\dfrac{\left(1-3x\right)^2}{6x^2+10x}\)
\(=\dfrac{9x^2+3x+2x-6x^2}{1+3x}.\dfrac{1-3x}{2x\left(3x+5\right)}\)
\(=\dfrac{3x^2+5x}{1+3x}.\dfrac{1-3x}{2x\left(3x+5\right)}\)
\(=\dfrac{x\left(3x+5\right)}{1+3x}.\dfrac{1-3x}{2x\left(3x+5\right)}\)
\(=\dfrac{1-3x}{2\left(1+3x\right)}\)
\(c,x=\dfrac{1}{3}\Rightarrow P=\dfrac{1-3.\dfrac{1}{3}}{2\left(1+3.\dfrac{1}{3}\right)}=\dfrac{1-1}{2.2}=0\)

x² - 6x + 9 - y²
= (x² - 6x + 9) - y²
= (x - 3)² - y²
= (x - 3 - y)(x - 3 + y)
= (x - y - 3)(x + y - 3)

A B C D E F K I G
a/
\(\widehat{BAE}+\widehat{DAE}=\widehat{BAD}=90^o\)
\(\widehat{DAF}+\widehat{DAE}=\widehat{FAE}=90^o\)
\(\Rightarrow\widehat{BAE}=\widehat{DAF}\) (cùng phụ với \(\widehat{DAE}\) ) (1)
\(AB=AD\) (cạnh hình vuông) (2)
Xét tg vuông ABE và tg vuông ADF
Từ (1) và (2) => tg ABE = tg ADF (Hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau)
\(\Rightarrow AE=AF\) (đpcm)
b/
AE=AF (cmt) => tg AEF là tg cân tại A
I là trung điểm EF (gt)
=> AI là trung tuyến thuộc EF => \(AI\perp EF\) (tring tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao)
\(\Rightarrow GK\perp EF\) (3)
Xét tg EIG và tg FIK có
\(\widehat{EIG}=\widehat{FIK}\) (góc đối đỉnh) (4)
EG//AB; AB//CD => EG//CD => EG//FK (5)
\(\Rightarrow\widehat{GEI}=\widehat{KFI}\) (góc so le trong) (6)
\(IE=IF\) (gt) (7)
Từ (4) (6) (7) => tg EIG = tg FIK (g.c.g) => EG = FK (8)
Từ (5) và (8) => EGFK là hình bình hành (Tứ giác có cặp cạnh đối // và = nhau là hình bình hành) (9)
Từ (3) và (9) => EGFK là hình thoi (hình bình hành có hai đường chéo vuông góc với nhau là hình thoi) (đpcm)
c/
Ta có tg AEF cân tại A (cmt); AI là trung tuyến thuộc EF (cmt)
=> AI là phân giác \(\widehat{EAF}\) (trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh)
Mà \(\widehat{EAF}=90^o\)
\(\Rightarrow\widehat{FAK}=45^o\)
\(\widehat{ACF}=45^o\)
\(\Rightarrow\widehat{FAK}=\widehat{ACF}=45^o\)
Xét tg AKF và tg ACF có
\(\widehat{FAK}=\widehat{ACF}=45^o\)
\(\widehat{AFC}\) chung
=> tg AKF đồng dạng với tg CAF (g.g.g)
d/

\(A=\dfrac{1}{x-2}+\dfrac{x^2-x}{x^2-7x+10}=\dfrac{2x-4}{x-5}\left(dk:x\ne2;x\ne5\right)\)
\(=\dfrac{1}{x-2}+\dfrac{x^2-x}{\left(x-2\right)\left(x-5\right)}=\dfrac{2x-4}{x-5}\)
\(=\dfrac{x-5+x^2-x-\left(2x-4\right)\left(x-2\right)}{\left(x-2\right)\left(x-5\right)}=0\)
\(\Leftrightarrow-5+x^2-2x^2+4x+4x-8=0\\ \Leftrightarrow-x^2+8x-13=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4+\sqrt{3}\\x=4-\sqrt{3}\end{matrix}\right.\) \(\left(tmdk\right)\)
Vậy ...

Bài `2`
\(a,\dfrac{1-x}{x+1}+3=\dfrac{2x+3}{x+1}\left(\text{đ}k\text{x}\text{đ}:x\ne-1\right)\\ \Leftrightarrow\dfrac{1-x}{x+1}+\dfrac{3\left(x-1\right)}{x+1}=\dfrac{2x+3}{x+1}\\ \Rightarrow1-x+3\left(x-1\right)=2x+3\\ \Leftrightarrow1-x+3x-3-2x-3=0\\ \Leftrightarrow-5=0\left(v\text{ô}.l\text{ý}\right)\)
\(b,\dfrac{1-6x}{x-2}+\dfrac{9x+4}{x+2}=\dfrac{x\left(3x-2\right)+1}{x^2-4}\)
\(\text{đ}k\text{x}\text{đ}\left\{{}\begin{matrix}x-2\ne0\\x+2\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne-2\end{matrix}\right.\)
\(\dfrac{1-6x}{x-2}+\dfrac{9x+4}{x+2}=\dfrac{x\left(3x-2\right)+1}{x^2-4}\)
\(\Leftrightarrow\dfrac{1-6x}{x-2}+\dfrac{9x+4}{x+2}=\dfrac{x\left(3x-2\right)+1}{\left(x-2\right)\left(x+2\right)}\\ \Leftrightarrow\dfrac{\left(1-6x\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{\left(9x+4\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{x\left(3x-2\right)+1}{\left(x-2\right)\left(x+2\right)}\\ \Rightarrow\left(1-6x\right)\left(x+2\right)+\left(9x+4\right)\left(x-2\right)=x\left(3x-2\right)+1\\ \Leftrightarrow x+2-6x^2-12x+9x^2-18x+4x-8-3x^2+2x-1=0\\ \Leftrightarrow-31x+1=0\\ \Leftrightarrow x=\dfrac{1}{31}\)
\(c,\left(x-1\right)\left(5x+3\right)=\left(3x-8\right)\left(x-1\right)\\ \Leftrightarrow\left(x-1\right)\left(5x+3\right)-\left(3x-8\right)\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(5x+3-3x+8\right)=0\\ \Leftrightarrow\left(x-1\right)\left(2x+11\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+11=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\2x=-11\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{11}{2}\end{matrix}\right.\)
a,x3+3x2+3x+1
b,x2+6x+9
c,-x3+9x2-27x+27
d,x2+4x+4
k,10x-25-x2
f,(x+y)2-9x2
g,8x3+42x2y+16xy2+6xy+y3

a) \(x^3+3x^2+3x+1=x^2+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3=\left(x-1\right)^3\)
b) \(x^2+6x+9=x^2+2\cdot3\cdot x+3^2=\left(x+3\right)^2\)
c) \(-x^3+9x^2-27x+27\)
\(=-\left(x^3-9x^2+27x-27\right)\)
\(=-\left(x^3-3\cdot3\cdot x^2+3\cdot3^2\cdot x-3^3\right)=-\left(x-3\right)^3\)
d) \(x^2+4x+4=x^2+2\cdot2\cdot x+2^2=\left(x+2\right)^2\)
k) \(10x-25-x^2=-x^2+10x-25=-\left(x^2-10x+25\right)\)
\(=-\left(x^2-2\cdot5\cdot x+5^2\right)=-\left(x-5\right)^2\)
f) \(\left(x+y\right)^2-9x^2=\left(x-y\right)^2-\left(3x\right)^2=\left[\left(x-y\right)-3x\right]\left[\left(x-y\right)+3x\right]\)
\(=\left(x-y-3x\right)\left(x-y+3x\right)=\left(-2x-y\right)\left(4x-y\right)\)

2A - (\(xy\) + 3\(x^2\) - 2y2) = \(x^2\) - 8y2 + \(xy\)
2A = \(x^2\) - 8y2 + \(xy\) + \(xy\) + 3\(x^2\) - 2y2
2A = (\(x^2\) + 3\(x^2\)) - (8y2 + 2y2) + (\(xy+xy\))
2A = 4\(x^2\) - 10y2 + 2\(xy\)
A = (4\(x^2\) - 10y2 + 2\(xy\)): 2
A = (2\(x^2\) - 5y2 + \(xy\)).2:2
A = 2\(x^2\) - 5y2 + \(xy\)

`@` `\text {Ans}`
`\downarrow`
\((x+ 3y)(x - 2у)\)
`= x(x-2y) + 3y(x-2y)`
`= x^2 - 2xy + 3xy - 6y^2`
`= x^2 + xy - 6y^2`

6a - [ b + 3a - (4a - b)]
= 6a - [ b + 3a - 4a + b]
= 6a - [2b - a]
= 6a - 2b + a
= 7a - 2b
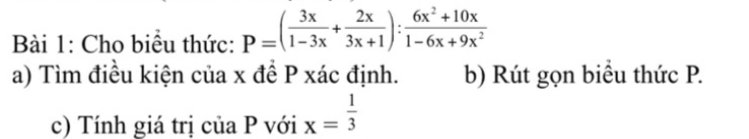

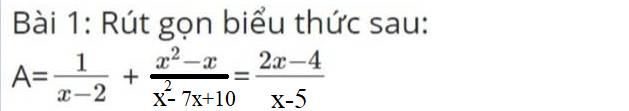

\(a,\dfrac{7-3x}{12}+\dfrac{3}{4}=2\left(x-2\right)+\dfrac{5\left(5-2x\right)}{6}\\ \Leftrightarrow\dfrac{7-3x+9-12.2\left(x-2\right)-2.5\left(5-2x\right)}{12}=0\\ \Leftrightarrow7-3x+9-24x+48-50+20x=0\\ \Leftrightarrow-7x=-14\\ \Leftrightarrow x=2\)
\(b,\dfrac{1}{x-1}+\dfrac{2}{x^2+x+1}=\dfrac{3x^2}{x^3-1}\left(dk:x\ne1\right)\\ \Leftrightarrow\dfrac{x^2+x+1+2\left(x-1\right)-3x^2}{x^3-1}=0\\ \Leftrightarrow x^2+x+1+2x-2-3x^2=0\\ \Leftrightarrow-2x^2+3x-1=0\\ \Leftrightarrow-2x^2+2x+x-1=0\\ \Leftrightarrow-2x\left(x-1\right)+\left(x-1\right)=0\\ \Leftrightarrow\left(-2x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-2x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(ktm\right)\\x=-\dfrac{1}{2}\left(tm\right)\end{matrix}\right.\)
\(c,\dfrac{7x-2}{3}-2x< 5-\dfrac{x-2}{4}\\ \Leftrightarrow\dfrac{4\left(7x-2\right)-12.2x-5.12+3\left(x-2\right)}{12}< 0\\ \Leftrightarrow28x-8-24x-60+3x-6< 0\\ \Leftrightarrow7x< 74\\ \Leftrightarrow x=\dfrac{74}{7}\)
\(c,2x-x\left(3x+1\right)< 15-3x\left(x+2\right)\\ \Leftrightarrow2x-3x^2-x-15+3x^2+6x< 0\\ \Leftrightarrow7x< 15\\ \Leftrightarrow x< \dfrac{15}{7}\)
hv